江西省抚州市南城县2022-2023学年七年级上学期期中考数学试卷
试卷更新日期:2022-11-22 类型:期中考试
一、单选题
-
1. 某正方体的每个面都有一个汉字,其平面展开图如图所示,那么在该几何体中和“博”字相对的字是( )
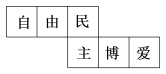 A、自 B、民 C、爱 D、由2. 如图,由6个相同的小正方体搭成的几何体,那么从左面看几何体的平面图形是( )
A、自 B、民 C、爱 D、由2. 如图,由6个相同的小正方体搭成的几何体,那么从左面看几何体的平面图形是( )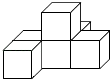 A、
A、 B、
B、 C、
C、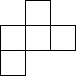 D、
D、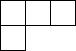 3. 2022年北京冬奥会国家速滑馆“冰丝带”是一座富含创新与节能理念的场馆,可容纳约12000名观众,将12000用科学记数法表示为( )A、 B、 C、 D、4. 有理数、在数轴上对应点的位置如图所示,下列各选项正确的是( )
3. 2022年北京冬奥会国家速滑馆“冰丝带”是一座富含创新与节能理念的场馆,可容纳约12000名观众,将12000用科学记数法表示为( )A、 B、 C、 D、4. 有理数、在数轴上对应点的位置如图所示,下列各选项正确的是( ) A、 B、 C、 D、5. 化简的结果是( )A、 B、 C、 D、6. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点 , 第二次将点向右移动6个单位长度到达点 , 第三次将点向左移动9个单位长度到达点 , ……按照这种移动规律进行下去,第30次移动到点 ,那么点所表示的数为( )
A、 B、 C、 D、5. 化简的结果是( )A、 B、 C、 D、6. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点 , 第二次将点向右移动6个单位长度到达点 , 第三次将点向左移动9个单位长度到达点 , ……按照这种移动规律进行下去,第30次移动到点 ,那么点所表示的数为( ) A、 B、46 C、 D、91
A、 B、46 C、 D、91二、填空题
-
7. 的系数是 .8. 负数的概念最早出现在中国古代著名的数学专著《九章算术》中,负数与对应的正数“数量相等,意义相反”,如果向东走了5米,记作+5米,那么向西走5米,可记作米.9. 若用平面分别截下列几何体:①三棱柱;②三棱锥;③正方体;④圆锥;⑤球,得到的截面不可能是三角形的是 . (填写正确的几何体前的序号)10. 化简: .11. 用“”定义新运算:对于任意有理数 , 都有 , 那么 .12. 数轴上表示点A的数是最大的负整数,则与点A相距4个单位长度的点表示的数是.
三、解答题
-
13. 计算题:(1)、(2)、14. 在-4,-3,-2,-1,1,2,3,4,m这9个数中,m代表一个数,你认为m是多少时,能够使这9个数分别填入图中的9个空格内,使每行的3个数、每列3个数、斜对角3个数个数相加均为零.
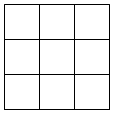 (1)、我认为m= .(2)、按要求将这9个数填入如图的空格内.15. 一个几何体由大小相同的立方块搭成,从上面看到的形状如图所示,其中小正方形中的数字表示在该位置的立方块个数.在所给的方框中分别画出该几何体从正面,从左面看到的形状图.
(1)、我认为m= .(2)、按要求将这9个数填入如图的空格内.15. 一个几何体由大小相同的立方块搭成,从上面看到的形状如图所示,其中小正方形中的数字表示在该位置的立方块个数.在所给的方框中分别画出该几何体从正面,从左面看到的形状图. 16. 已知 , 求17. 已知多项式M= .(1)、当x=1,y=2,求M的值;(2)、若多项式M与字母x的取值无关,求y的值.18. 七年级学生在5名教师的带领下去公园秋游,公园的门票为每人30元,现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都按折收费.若有名学生去公园秋游.(1)、用含的代数式表示两种优惠方案各需多少元?(2)、当时,采用哪种方案优惠?请说明理由.19. 已知 , 求代数式的值.20. 如图所示,池塘边有块长为20米,宽为10米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地.
16. 已知 , 求17. 已知多项式M= .(1)、当x=1,y=2,求M的值;(2)、若多项式M与字母x的取值无关,求y的值.18. 七年级学生在5名教师的带领下去公园秋游,公园的门票为每人30元,现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都按折收费.若有名学生去公园秋游.(1)、用含的代数式表示两种优惠方案各需多少元?(2)、当时,采用哪种方案优惠?请说明理由.19. 已知 , 求代数式的值.20. 如图所示,池塘边有块长为20米,宽为10米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地. (1)、用含x的式子表示菜地的周长.(2)、求当米时,菜地的周长.21. 如图所示,一只蚂蚁从点A沿数轴向右直爬3个单位长度到达点B,点A表示数 , 设点B所表示的数为m.
(1)、用含x的式子表示菜地的周长.(2)、求当米时,菜地的周长.21. 如图所示,一只蚂蚁从点A沿数轴向右直爬3个单位长度到达点B,点A表示数 , 设点B所表示的数为m.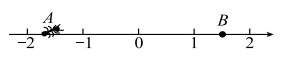 (1)、求m的值;(2)、求的值.22. 学校组织同学到博物馆参观,小明因事没有和同学同时出发,于是准备在学校门口搭乘出租车赶去与同学们会合,出租车的收费标准是:起步价为7元,3千米后每千米收元,不足1千米的按1千米计算.请你回答下列问题:(1)、小明乘车千米,应付费元.(2)、小明乘车 (是大于3的整数千米,应付费多少钱?(3)、小明身上仅有元钱,乘出租车到距学校9千米远的博物馆的车费够不够?请说明理由.23. 如图,在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,C满足 .
(1)、求m的值;(2)、求的值.22. 学校组织同学到博物馆参观,小明因事没有和同学同时出发,于是准备在学校门口搭乘出租车赶去与同学们会合,出租车的收费标准是:起步价为7元,3千米后每千米收元,不足1千米的按1千米计算.请你回答下列问题:(1)、小明乘车千米,应付费元.(2)、小明乘车 (是大于3的整数千米,应付费多少钱?(3)、小明身上仅有元钱,乘出租车到距学校9千米远的博物馆的车费够不够?请说明理由.23. 如图,在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,C满足 . (1)、a= , b= , c= .(2)、①若将数轴折叠,使得A点与C点重合,则点B与数 ▲ 表示的点重合;
(1)、a= , b= , c= .(2)、①若将数轴折叠,使得A点与C点重合,则点B与数 ▲ 表示的点重合;②点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,则t秒钟时,则AC= ▲ (用含的代数式表示).
(3)、在(2)②的条件下,请问:3BC-2AB的值是否随着时间t的变化而变化?若变化,请说明理由:若不变,请求其值.