黑龙江省鸡西市2022-2023学年七年级上学期期中数学试卷

试卷更新日期：2022-11-22 类型：期中考试

进入出卷网下载

一、单选题

1. 如果 $| a | = - a$ ，那么a一定是（）

A、正数 B、负数 C、非正数 D、非负数

查看试题解析
2. 单项式-3²xy²z³的系数和次数分别是（）

A、-1，8 B、-3，8 C、-9，6 D、-9，3

查看试题解析
3. 用四舍五入按要求对0.05019分别取近似值，其中错误的是（）

A、0.1精确到0.1 B、0.05精确到百分位 C、0.05精确到千分位 D、0.0502精确到0.0001

查看试题解析
4. 计算 $(- 6) \times (- \frac{1}{2})$ 的结果是（）

A、12 B、 $- 12$ C、 $- 3$ D、3

查看试题解析
5. $- 2022$ 的相反数是（）

A、 $- 2022$ B、 $- \frac{1}{2022}$ C、 $\frac{1}{2022}$ D、2022

查看试题解析
6. 下列说法错误的是（）

A、0既不是正数，也不是负数 B、1是绝对值最小的有理数 C、一个有理数不是整数就是分数 D、0的绝对值是0

查看试题解析
7. 下列互为倒数的是（）

A、 $3$ 和 $\frac{1}{3}$ B、 $- 2$ 和 $2$ C、 $3$ 和 $- \frac{1}{3}$ D、 $- 2$ 和 $\frac{1}{2}$

查看试题解析
8. 按一定规律排列的单项式：a，﹣a² ， a³ ， ﹣a⁴ ， a⁵ ， ﹣a⁶ ， ……，第n个单项式是（）

A、aⁿ B、﹣aⁿ C、（﹣1）ⁿ⁺¹aⁿ D、（﹣1）ⁿaⁿ

查看试题解析
9. 已知一个单项式的系数为-3，次数为4，这个单项式可以是（）

A、 $3 x y$ B、 $3 x^{2} y^{2}$ C、 $- 3 x^{2} y^{2}$ D、 $4 x^{3}$

查看试题解析
10. a、b是有理数，它们在数轴上的对应点的位置如图所示，把a、－a、b、－b按从小到大的顺序排列为（）

A、－b＜－a＜a＜b B、－a＜－b＜a＜b C、－b＜a＜－a＜b D、－b＜b＜－a＜a

查看试题解析
11. 若 $- 2 a^{m} b^{2 m + n}$ 与 $5 a^{n + 2} b^{2 m + n}$ 可以合并成一项，则m-n的值是（）

A、2 B、0 C、-1 D、1

查看试题解析
12. 两个形状大小完全相同的长方形中放入4个相同的小长方形后，得到图①和图②的阴影部分，如果大长方形的长为m，则图②与图①的阴影部分周长之差是（）

A、 $- \frac{m}{2}$ B、 $\frac{m}{2}$ C、 $\frac{m}{3}$ D、 $- \frac{m}{3}$

查看试题解析
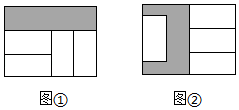13. 如图，用若干根相同的小木棒拼成图形，拼第1个图形需要6根小木棒，拼第2个图形需要14根小木棒，拼第3个图形需要22根小木棒……若按照这样的方法拼成的第n个图形需要2022根小木棒，则n的值为（）

A、252 B、253 C、336 D、337

查看试题解析

二、填空题

14. 袁隆平院士被誉为“杂交水稻之父”，经过他带领的团队多年努力，目前我国杂交水稻种植面积约为2.5亿亩.将250000000用科学记数法表示为 $2.5 \times 10^{n}$ ，则 $n =$ .

查看试题解析
15. 单项式 $- \frac{π a^{2} b}{2}$ 的系数是．

查看试题解析
16. 规定一种新运算“☆”对于任意两个有理数a和b，有a☆b＝a-b+1，请你根据新运算，计算（2☆3）☆2的值是

查看试题解析
17. 在数4.3， $- \frac{3}{5}$ ，｜0｜， $- (- \frac{22}{7})$ ， -｜-3｜，-（+5）中，是正数

查看试题解析
18. 若多项式 $5 x^{2} - m x y - y^{2} + 7 x y - 1$ （m为常数）不含 $x y$ 项，则 $m =$ ．

查看试题解析
19. 按一定规律排列的数据依次为 $\frac{1}{2}$ ， $\frac{4}{5}$ ， $\frac{7}{10}$ ， $\frac{10}{17}$ ……按此规律排列，则第30个数是．

查看试题解析
20. 若（x-1）⁴（x+2）⁵=a₀+a₁x+a₂x²+…+ a₉x⁹ ，求：a₁+a₃+a₅+a₇+a₉= ．

查看试题解析

三、解答题

21. 计算：

(1)、1.25÷（-0.5）÷（-2 $\frac{1}{2}$ ）×1；

(2)、（-81）÷（＋3 $\frac{1}{4}$ ）×（- $\frac{4}{9}$ ）÷（-1 $\frac{1}{13}$ ）；

(3)、 $(2 \frac{1}{3}) - (10 \frac{1}{3}) + (- 8 \frac{1}{5}) - (+ 3 \frac{2}{5})$ ；

(4)、 $- 8721 + 53 \frac{19}{21} - 1279 + 43 \frac{2}{21}$ ；

(5)、 $5 x y - \frac{3}{2} x^{3} y^{2} - 4 x y + \frac{1}{2} y^{2} x^{3} - \frac{1}{2} x y - 3 x^{3} y^{2}$ ；

(6)、 $2 (3 a^{2} b - a b^{2}) - 3 (2 a^{2} b + 1) - 3 a b^{2} + 3$ ．

查看试题解析
22. 先化简，再求值：

(1)、 $- 3 (x^{2} - 2 x) + 2 (\frac{3}{2} x^{2} - 2 x - \frac{1}{2})$ ，其中 $x = 4$ ；

(2)、 $7 x^{2} y - [6 x y^{2} - 5 (x y^{2} + \frac{3}{4} x^{2} y) - \frac{2}{3} x y^{2}] - x y^{2}$ ，其中 $x = 2$ ， $y = - 1$ ．

(3)、 $5 x^{2} - 2 (3 y^{2} + 6 x y) + (2 y^{2} - 5 x^{2})$ ，其中 $x = \frac{1}{3}$ ， $y = - \frac{1}{2}$ ；

(4)、设 $A = 3 a^{2} + 4 a b + 5$ ， $B = a^{2} - 2 a b$ ．当 $a$ ， $b$ 互为倒数时，求 $A - 3 B$ 的值．

查看试题解析
23. 已知 $A = 5 x^{2} - m x + n$ ， $B = - 3 y^{2} + 2 x - 1$ ，若 $A + B$ 中不含一次项和常数项，求 $2 (m^{2} n - 1) - 5 m^{2} n + 4$ 的值．

查看试题解析
24. 如图，已知数轴上有A、B、C三个点，它们表示的数分别是-24，-10，10．

(1)、填空：AB＝， BC＝；

(2)、若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒3个单位长度和5个单位长度的速度向右运动．设运动时间为t，用含t的代数式表示运动后BC和AB的长，是否存在符合要求的m的值，使BC-mAB的值不随时间t的变化而变化，若存在，求出m的值，若不存在，说明理由．

查看试题解析
25. 阅读理解：整体代换是一种重要的数学思想方法．例如：计算 $2 (2 m + n) - 5 (2 m + n) + (2 m + n)$ 时，可将 $(2 m + n)$ 看成一个整体，合并同类项得 $- 2 (2 m + n)$ ，再利用分配律去括号得 $- 4 m - 2 n$ ．

(1)、若已知 $2 m + n = 2$ ，请你利用整体代换思想求代数式 $6 m + 3 n - 10$ 的值；

(2)、一正方形边长为 $2 m + n$ ，将此正方形的边长均增加1之后，其面积比原来正方形的面积大9，求 $2 m + n$ 的值．

查看试题解析