广东省深圳市宝安区2022-2023学年七年级上学期期中考试数学试题

试卷更新日期：2022-11-22 类型：期中考试

进入出卷网下载

一、单选题

1. 在 $- 3 ， - 1 ， 0 ， 2$ 这四个数中，绝对值最小的数是（）

A、0 B、 $- 1$ C、-3 D、2

查看试题解析
2. 据统计，2022年考研报名人数约有457万，创下历史新高，把457万用科学记数法表示为（）

A、 $4.57 \times 1 0^{6}$ B、 $45.7 \times 1 0^{6}$ C、 $4.57 \times 1 0^{7}$ D、 $0.457 \times 1 0^{7}$

查看试题解析
3. 下列几何体的截面不可能是圆的是（）

A、圆柱 B、圆台 C、棱柱 D、圆锥

查看试题解析
4. 下列选项中的两个式子不是同类项的是（）

A、 $- a^{2} b$ 与 $\frac{1}{2} a^{2} b$ B、 $\frac{1}{2} x$ 与 $- 3 x$ C、 $y x$ 与 $- x y$ D、 $- \frac{1}{3} a^{2} b$ 与 $\frac{1}{5} a b^{2}$

查看试题解析
5. 在数轴上，表示数 $a$ 的点在原点的左侧，则表示下列各数的点，也在原点左侧的是（）

A、 $- a$ B、 $- 2 a + 1$ C、 $3 a$ D、 $a^{2}$

查看试题解析
6. 一个正方体的表面展开图如图所示，六个面上各有一字，连起来的意思是“全面落实双减”，把它折成正方体后，与“全”相对的字是（）

A、双 B、减 C、落 D、面

查看试题解析
7. 若一长方形的周长为30，长用字母x表示，则此长方形的面积为（）

A、x（30-2x） B、x（30-x） C、x（15-x） D、x（15+x）

查看试题解析
8. 若多项式ax²+2x-y²-7与x²-bx-3y²+1的差与x的取值无关，则a-b的值为（）

A、1 B、-1 C、3 D、-3

查看试题解析
9. 下列说法正确的个数有（）

(1)、若 $a^{2} = b^{2}$ ，则 $| a | = | b |$ ；（2）若a，b互为相反数，则 $\frac{a}{b} = - 1$ ；（3）绝对值相等的两数相等；（4）单项式 $7 \times 1 0^{2} a^{4}$ 的次数是6；（5） $- a$ 一定是一个负数．

A、4 B、3 C、2 D、1

查看试题解析
10. 任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和，如： $2^{3} = 3 + 5$ ， $3^{3} = 7 + 9 + 11$ ， $4^{3} = 13 + 15 + 17 + 19$ ， …按此规律，若 $m^{3}$ 分裂后，其中有一个奇数是2023，则m的值是（）

A、46 B、45 C、44 D、43

查看试题解析

二、填空题

11. 钟表上的时针转动一周形成一个圆面，这说明了．

查看试题解析
12. 若有理数a，b满足 $| a + 3 | + (b - 4)^{2} = 0$ ，则 $a b =$ ．

查看试题解析
13. 已知单项式 $- 2 m^{2 x} n$ 与 $3 m^{6} n^{y}$ 是同类项，则 $y^{x}$ ＝．

查看试题解析
14. 若 $x - 3 y = 3$ ，则代数式 $4 - 2 x + 6 y$ 的值是．

查看试题解析
15. 有理数a、b、c在数轴上的对应点如图所示，化简： $| b | - | c + b | + | a - c | =$ ．

查看试题解析

三、解答题

16. 计算：

(1)、 $27 - 13 + (- 4) - 32$ ；

(2)、 $(- 9) \div (- \frac{3}{4}) \times (- \frac{4}{3})$ ；

(3)、 $(- \frac{3}{4} - \frac{5}{6} + \frac{5}{8}) \times (- 24)$ ；

(4)、 $- 1^{4} - \frac{1}{6} \times [5 - {(- 3)}^{2}]$ ．

查看试题解析
17. 先化简，再求值： $5 a^{2} b - [2 a b - 3 (a b - \frac{7}{3} a^{2} b) + a b]$ ，其中 $a ＝ 4$ ， $b = \frac{1}{4}$ ．

查看试题解析
18. 如图是由棱长都为 $1 c m$ 的6块小正方体组成的简单几何体．

请在方格中画出该几何体的三个视图．

查看试题解析
19. 随着手机的普及，微信的兴起，许多人做起了“微商”，很多农产品也改变了原来的销售模式，实行了网上销售．刚大学毕业的小明把自家的冬枣产品也放到了网上实行包邮销售，他原计划每天卖100斤冬枣，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某周的销售情况（超额记为正，不足记为负．单位：斤）；
星期
一
二
三
四
五
六
日
与计划量的差值
$+ 4$
$- 3$
$- 5$
$+ 14$
$- 8$
$+ 21$
$- 6$

(1)、根据记录的数据可知销售量最多的一天比销售量最少的一天多销售斤；

(2)、本周实际销售总量是否达到了计划数量？试说明理由；

(3)、若冬枣每斤按8元出售，每斤冬枣需要小明支付的平均运费是3元，那么小明本周销售冬枣实际共得多少元？

查看试题解析
20. 某中学一教室前有一块长为12米，宽为 $4 x$ 米的长方形空地，学校向全校师生征集这块地的绿化设计方案并要求绿地面积大于这块地总面积的 $\frac{5}{8}$ ，如图是学生小明的设计方案，阴影部分是绿地.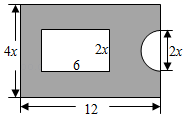

(1)、用含x的式子分别表示这块空地的总面积及绿地的面积(结果保留 $π$ ).

(2)、若 $x = 2$ 米时，试问小明的设计方案是否合乎要求？请说明理由(其中 $π$ 取3).

查看试题解析
21. 相传大禹治水时，“洛水”中出现了一个神龟，其背上有美妙的图案，史称“洛书”．用现在的数字翻译出来，就是三阶幻方．三阶幻方是最简单的幻方，又叫九宫格，其对角线、横行、纵向的数字之和均相等，这个和叫做幻和，正中间那个数叫中心数，且幻和恰好等于中心数的3倍．如图1，是由1、2、3、4、5、6、7、8、9所组成的一个三阶幻方，其幻和为15，中心数为5．

(1)、如图2所示，则幻和＝；

(2)、若 $b = 4$ ， $c = 6$ ，求a的值；

(3)、由三阶幻方可以衍生出许多有特定规律的新幻方．在如图3所示的“幻方”中，每个小三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等，当 $x = 2$ ， $y = - 3$ 时，则 $a - b - c + d$ 的值为多少？

查看试题解析
22. 定义：数轴上有两点A，B，如果存在一点C，使得线段 $A C$ 的长度是线段 $B C$ 的长度的2倍，那么称点C为线段 $A B$ 的“幸运点”．

(1)、如图①，若数轴上A，B两点所表示的数分别是 $- 2$ 和4，点C为线段 $A B$ 上一点，且点C为线段 $A B$ 的“幸运点”，则点C表示的数为；

(2)、如图②，若数轴上A，B两点所表示的数分别是 $- 4$ 和 $- 1$ ，点C为数轴上一点，若点C为线段 $A B$ 的“幸运点”，则点C表示的数为；

(3)、如果数轴上点A表示的数是2001，点B表示的数是2025，动点P从点A出发以每秒2个单位的速度向右匀速运动，设运动的时间为t秒．当t为何值时，点P是线段 $A B$ 的“幸运点”．

查看试题解析

星期	一	二	三	四	五	六	日
与计划量的差值	$+ 4$	$- 3$	$- 5$	$+ 14$	$- 8$	$+ 21$	$- 6$