广东省梅州市大埔县2022-2023年七年级上学期期中教学质量监测数学试题

试卷更新日期：2022-11-22 类型：期中考试

进入出卷网下载

一、单选题

1. 2022的倒数是（）

A、 $- 2022$ B、2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 数字 $336000$ 科学记数法表示为（）

A、 $0.336 \times 1 0^{6}$ B、 $3.36 \times 1 0^{6}$ C、 $3.36 \times 1 0^{5}$ D、 $33.6 \times 1 0^{4}$

查看试题解析
3. 如图是某几何体的从三个不同方向看到的图形，则这个几何体是（）

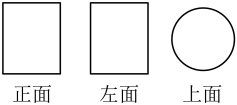A、圆柱 B、正方体 C、球 D、圆锥

查看试题解析
4. a，b是有理数，它们在数轴上的对应点的位置如图所示，把a，b，0，按照从大到小的顺序排列，正确的是（）

A、 $a > b > 0$ B、 $a > 0 > b$ C、 $b > a > 0$ D、 $b > 0 > a$

查看试题解析
5. 下列各式计算正确的是（）

A、 $6 a + a = 7 a^{2}$ B、 $- 2 a + 5 b = 3 a b$ C、 $4 m^{2} n - 2 m n^{2} = 2 m$ D、 $3 a b^{2} - 5 b^{2} a = - 2 a b^{2}$

查看试题解析
6. 如图是每个面上都有一个汉字的正方体的一种展开图，那么在原正方体的表面上，与汉字“强“相对的面上的汉字是（）

A、主 B、文 C、民 D、富

查看试题解析
7. 若代数式y²-2y+1的值是5，则代数式2y²-4y-5的值是（）

A、-3 B、25 C、-25 D、3

查看试题解析
8. 下列说法中正确的是（）

A、－a一定小于0 B、任何有理数的绝对值都是正数 C、如果两个数互为相反数，那么它们的绝对值相等 D、最大的负有理数是－1

查看试题解析
9. 某企业去年产值p万元，今年比去年增产10%，今年产值是（）

A、p（1+10%）万元 B、（p+10%）万元 C、 $\frac{p}{1 + 10 %}$ 万元 D、 $\frac{p}{1 - 10 %}$ 万元

查看试题解析
10. 如图，题中图形是用棋子按照一定规律摆成的，按照这种摆法，第n个图形中共有棋子（）

A、2n枚 B、（n²+1）枚 C、（n²-n）枚 D、（n²+n）枚

查看试题解析

二、填空题

11. 如果收入10元记作+10元，那么支出80元记作元．

查看试题解析
12. 单项式 $- \frac{3 π^{2} a b^{3} c^{2}}{2}$ 的次数是．

查看试题解析
13. 数轴上一点A，它所对应的数字为﹣1，将点A向左移动2个单位长度达到点B，再向右移动5个单位长度到达点C．则点C表示的数为．

查看试题解析
14. 长方形的长为 $2 b - a$ ，宽比长少 $b$ ，则这个长方形的周长是．

查看试题解析
15. 一个几何体由若干大小相同的小立方块搭成，如图分别是从它的正面、上面看到的形状图，则该几何体至少是用个小立方块搭成的．

查看试题解析
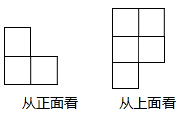16. 若x为有理数，则 $5 - | x - 2 |$ 的最大值为

查看试题解析
17. 对于有理数a，b定义一种新运算“⊙”，规定a⊙b=|a+b|+|a﹣b|，则2⊙（﹣3）= ．

查看试题解析

三、解答题

18. 在数轴上画出表示下列各数的点，并把它们用“<”连接起来．
$- | - 2.5 |$ ， $- 3 \frac{1}{2}$ ， $- (+ 1)$ ， $- 2$ ， $- (- 0.5) 3$ ， 3

查看试题解析
19. 计算： $(- 7) - (- 11) - 6 + (- 5)$

查看试题解析
20. 计算： $- 1^{2022} + \frac{27}{4} \times (- \frac{1}{3} - 1) \div {(- 3)}^{2}$ ．

查看试题解析
21. 妈妈给圆柱形的玻璃杯（底面直径16cm，高20cm）做了一个布套（包住侧面）

(1)、求出至少用布料多少平方厘米？

(2)、求这个杯子最多可以盛水多少立方厘米？

查看试题解析
22. 如图，是由一些棱长为1的相同的小正方体组合成的简单几何体．请分别画出该几何体从正面看、从左面看和从上面看所得到的图形．

查看试题解析
23. 先化简，再求值：已知 $A = 3 a^{2} + b^{2} - 5 a b$ ， $B = 2 a b - 3 b^{2} + 4 a^{2}$ ，

(1)、化简 $2 A - B$ ．

(2)、当 $a = - 1$ ， $b = 2$ 时，求 $2 A - B$ 的值．

查看试题解析
24. 某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下（规定向南为正，向北为负，单位：km）：

第1批

第2批

第3批

第4批

第5批

5km

2km

﹣4km

﹣3km

10km

(1)、接送完第5批客人后，该驾驶员在公司的什么方向，距离公司多少千米？

(2)、若该出租车每千米耗油0.1升，那么在这过程中共耗油多少升？

(3)、若该出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？

查看试题解析
25. 某零件厂现生产A ， B两种尺寸的零件，两种零件的成本和售价如表：

成本（元/个）

售价（元/个）

A

50

80

B

70

90

该厂每天共生产A ， B两种尺寸的零件800个，设每天生产A种零件x个．

(1)、用含x的代数式表示该厂每天的生产成本，并进行化简；

(2)、用含x的代数式表示该厂每天获得的利润，并进行化简；

(3)、当x＝500时，求该厂每天获得的利润．（利润＝售价﹣成本）

查看试题解析

第1批	第2批	第3批	第4批	第5批
5km	2km	﹣4km	﹣3km	10km

	成本（元/个）	售价（元/个）
A	50	80
B	70	90