浙江省衢州市开化县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-22 类型:期末考试
一、单选题
-
1. 已知的半径为2,点到圆心的距离为1.5,则点在( )A、圆外 B、圆上 C、圆内 D、不能确定2. 一个口袋里装有4个白球,5个黑球,除颜色外,其余如材料、大小、质量等完全相同,随意从中抽出一个球,抽到白球的概率是( )A、 B、 C、 D、3. 二次函数y=﹣3(x+1)2﹣7有( )A、最大值﹣7 B、最小值﹣7 C、最大值7 D、最小值74. 两个相似三角形的面积之比为 , 其中较小三角形的周长为4,则另一个三角形的周长为( )A、16 B、8 C、2 D、15. 在Rt△ABC中,∠C=90°,AC=4,BC=3,则下列选项正确的是( )A、sinA= B、cosA= C、cosB= D、tanB=6. 如图,直线 , 直线分别交 , , 于点 , , , 直线分别交 , , 于点 , , .已知 , , , 则的长为( )
 A、2 B、3 C、 D、47. 如图,点A , B , C , D在⊙O上, ,点B是 的中点,则 的度数是( )
A、2 B、3 C、 D、47. 如图,点A , B , C , D在⊙O上, ,点B是 的中点,则 的度数是( )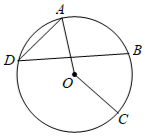 A、 B、 C、 D、8. 已知 , , 均是抛物线上的点,则( )A、 B、 C、 D、9. 《九章算术》被尊为古代数学“群经之首”,其卷九勾股定理篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这个木材,锯口深等于1寸,锯道长1尺,则圆形木材的直径是( )(1尺=10寸)
A、 B、 C、 D、8. 已知 , , 均是抛物线上的点,则( )A、 B、 C、 D、9. 《九章算术》被尊为古代数学“群经之首”,其卷九勾股定理篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这个木材,锯口深等于1寸,锯道长1尺,则圆形木材的直径是( )(1尺=10寸) A、12寸 B、13寸 C、24寸 D、26寸10. 如图,在中, , 中线 , 相交于点. , 交于点. , 则的长为( )
A、12寸 B、13寸 C、24寸 D、26寸10. 如图,在中, , 中线 , 相交于点. , 交于点. , 则的长为( )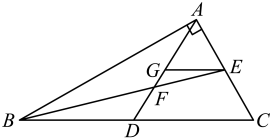 A、5 B、6 C、10 D、12
A、5 B、6 C、10 D、12二、填空题
-
11. 二次函数 y=2(x-3)2+1图象的顶点坐标是.12. 已知一个正多边形的一个内角是120º,则这个多边形的边数是 .13. “头盔是生命之盔”,质检部门对某工厂生产的头盔质量进行抽查,抽查结果如下表:
抽查的头盔数
100
200
300
500
800
1000
3000
合格的头盔数
95
194
289
479
769
960
2880
合格头盔的频率
0.950
0.945
0.962
0.958
0.961
0.960
0.960
请估计该工厂生产10000个头盔,合格的头盔数有个.
14. 如图,已知抛物线 的顶点为点A,交轴于点.轴,与抛物线交于点 , 若将该抛物线进行平移,使顶点落在点处,则平移后的抛物线表达式为.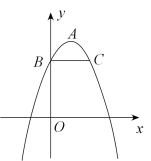 15. 如图,是的角平分线, , , .则的长为.
15. 如图,是的角平分线, , , .则的长为. 16. 如图,为等边的外接圆,点为上一动点,连结 , .为上位于右边的一条弦,且 , 连结 , 则与所在直线的夹角度数为°.当时, , 此时的半径为.
16. 如图,为等边的外接圆,点为上一动点,连结 , .为上位于右边的一条弦,且 , 连结 , 则与所在直线的夹角度数为°.当时, , 此时的半径为.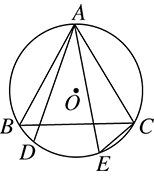
三、解答题
-
17. 计算:18. 防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.(1)、小明从A测温通道通过的概率是;(2)、利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.19. 如图,在的正方形网格中(每个小正方形的边长都为1),点 , , 均在格点上.
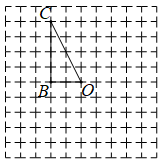 (1)、在网格图中画出绕点顺时针旋转90°后的.(2)、在(1)的条件下,求旋转过程中,点所经过的弧长.(结果保留)20. 如图,在中,点 , , 分别在 , , 上, , .
(1)、在网格图中画出绕点顺时针旋转90°后的.(2)、在(1)的条件下,求旋转过程中,点所经过的弧长.(结果保留)20. 如图,在中,点 , , 分别在 , , 上, , .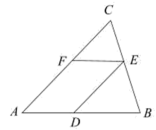 (1)、求证:.(2)、若 , 的面积为9,求的面积.21. 如图,为了测量全国5A级景区根博园内醉根塔的高度,小凯采用了如下的方法:先从与醉根塔底端在同一水平线上的点出发.沿斜坡行走65米至坡顶处,再从处沿水平方向继续前行若干米后至点处,在点测得醉根塔顶端的仰角为60°,醉根塔底端的俯角为45°,点 , , , , 在同一平面内,斜坡的坡比.根据小凯的测量数据,求:
(1)、求证:.(2)、若 , 的面积为9,求的面积.21. 如图,为了测量全国5A级景区根博园内醉根塔的高度,小凯采用了如下的方法:先从与醉根塔底端在同一水平线上的点出发.沿斜坡行走65米至坡顶处,再从处沿水平方向继续前行若干米后至点处,在点测得醉根塔顶端的仰角为60°,醉根塔底端的俯角为45°,点 , , , , 在同一平面内,斜坡的坡比.根据小凯的测量数据,求: (1)、坡顶到地面的距离.(2)、醉根塔的高度(精确到0.1米,).22. 如图,已知是直径,且. , 是上的点, , 交于点 , 连结 , .
(1)、坡顶到地面的距离.(2)、醉根塔的高度(精确到0.1米,).22. 如图,已知是直径,且. , 是上的点, , 交于点 , 连结 , .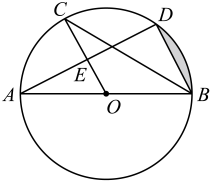 (1)、求的度数.(2)、求出的长度.(3)、求出图中阴影部分的面积(结果保留).23. 某奶茶店近期推出一款新品奶茶,该款奶茶的制作成本为5元/杯.据市场调查分析,在一个月内,销售单价定为15元时,月销售量为750杯;销售单价每上涨1元,月销售量就减少50杯.设销售单价为元,月销售量为杯,月获利为元(月获利=月销售额-月成本).(1)、写出与之间的函数关系式.(2)、当销售单价为多少元时,月获利为5000元?(3)、因奶茶原料库存较多,必须保证月销售量不低于650杯,则销售单价为多少元时,月获利最大,最大月获利为多少?24. 在矩形中, , , 点为上的点,且 , 连结.点为的中点,点为上的一动点,连结 , 过点作 , 交或于点 , 连结.
(1)、求的度数.(2)、求出的长度.(3)、求出图中阴影部分的面积(结果保留).23. 某奶茶店近期推出一款新品奶茶,该款奶茶的制作成本为5元/杯.据市场调查分析,在一个月内,销售单价定为15元时,月销售量为750杯;销售单价每上涨1元,月销售量就减少50杯.设销售单价为元,月销售量为杯,月获利为元(月获利=月销售额-月成本).(1)、写出与之间的函数关系式.(2)、当销售单价为多少元时,月获利为5000元?(3)、因奶茶原料库存较多,必须保证月销售量不低于650杯,则销售单价为多少元时,月获利最大,最大月获利为多少?24. 在矩形中, , , 点为上的点,且 , 连结.点为的中点,点为上的一动点,连结 , 过点作 , 交或于点 , 连结. (1)、如图1,当点与点重合时,求的长.(2)、如图2,当时,求的长.(3)、如图3,点从点出发,当的长为时,点停止运动.请直接写出的中点的运动路径长.
(1)、如图1,当点与点重合时,求的长.(2)、如图2,当时,求的长.(3)、如图3,点从点出发,当的长为时,点停止运动.请直接写出的中点的运动路径长.