浙江省宁波市江北区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-22 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $\frac{a}{b} = \frac{2}{5}$ ，则 $\frac{a}{a + b} =$ （）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2}{7}$ D、 $\frac{3}{7}$

查看试题解析
2. 如图是某几何体的表面展开图，该几何体是（）

A、长方体 B、圆柱 C、圆锥 D、直三棱柱

查看试题解析
3. 下列事件中是不可能事件的是（）

A、从一副扑克牌中任抽一张牌恰好是“红桃” B、在装有白球和黑球的袋中摸球，摸出了红球 C、2022年大年初一早晨艳阳高照 D、从两个班级中任选三名学生，至少有两名学生来自同一个班级

查看试题解析
4. 如图，在Rt $△ A B C$ 中， $∠ C = 90 ° ， c o s A = \frac{1}{3}$ ，则 $s i n B$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2 \sqrt{2}}{3}$ D、 $2 \sqrt{2}$

查看试题解析
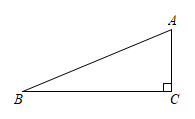5. 关关于二次函数y=-2（x-2）²+1的图像，下列叙述不正确的是（）

A、对称轴为直线x=2 B、顶点坐标为（-2，1） C、开口向下 D、与x轴有两个交点

查看试题解析
6. 已知圆与直线有两个公共点，且圆心到直线的距离为4，则该圆的半径可能为（）

A、2 B、3 C、4 D、5

查看试题解析
7. 下列与相似有关的命题中，正确的是（）
①所有的等腰三角形都相似；②所有的矩形都相似；③所有的正六边形都相似.

A、①②③ B、① C、② D、③

查看试题解析
8. 如图， $A B$ 是半圆 $O$ 的直径， $C 、 D$ 是半圆上两点，且满足 $∠ A D C = 120 ° ， B C = 1$ ，则 $\overset{�}{B C}$ 的长为（）

A、 $\frac{π}{3}$ B、 $\frac{π}{4}$ C、 $\frac{π}{6}$ D、 $\frac{2 π}{3}$

查看试题解析
9. 如图，点 $I$ 是 $△ A B C$ 的重心， $S_{△ A B C} = 9$ ，将 $∠ B A C$ 平移使其顶点与点 $I$ 重合，则图中阴影部分的面积为（）

A、6 B、 $7.5$ C、8 D、 $8.5$

查看试题解析
10. 如图，在等边 $△ A B C$ 中， $A B = 4$ ，点 $D$ 为 $A B$ 的中点，动点 $E 、 F$ 分别在 $A D 、 B C$ 上，且 $E F = 2 \sqrt{3}$ ，作 $△ B E F$ 的外接圆 $⊙ O$ ，交 $A C$ 于点 $G 、 H$ .当动点 $E$ 从点 $D$ 向点 $A$ 运动时，线段 $G H$ 长度的变化情况为（）

A、一直不变 B、一直变大 C、先变小再变大 D、先变大再变小

查看试题解析

二、填空题

11. 请你用数学的眼光观察，以下历届冬奥会图标中，你最为欣赏的图标是，（选择①，②，③，④中的一项）选择理由是.

查看试题解析
12. 圆柱的底面半径为 $1 c m$ ，母线长为 $5 c m$ ，则该圆柱的侧面积为 $c m^{2}$ .

查看试题解析
13. 某企业对其生产的产品进行抽检，抽检结果如下表：
抽检件数
5
50
100
500
1000
2000
3000
5000
不合格件数
0
1
2
9
21
40
60
100
不合格频率
0
$0.02$
$0.02$
$0.018$
$0.021$
$0.02$
$0.02$
$0.02$
则该产品不合格的概率约为.

查看试题解析
14. 如图，正五边形的外接圆半径为1cm，则边长AB≈cm.（精确到0.1cm）（参考数据：sin36°≈0.6，cos36°≈0.8，tan36°≈0.7）

查看试题解析
15. 将二次函数 $y = - x^{2} + m x + n$ （m，n为常数）的图象，先向左平移1个单位长度，再向上平移2个单位长度后，得到的图象顶点为 $(0 ， 4)$ ，则 $m + n$ 的值为.

查看试题解析
16. 如图，在Rt $△ A B C$ 中， $∠ B A C = 90 °$ ，点 $D$ 为 $A C$ 上一点，连结 $B D$ ，若 $∠ D B C = 45 °$ ，则 $\frac{A D}{C D}$ 的最大值为.

查看试题解析

三、解答题

17. 计算： $\sqrt{3} t a n 30 ° + 2 c o s 60 ° - \sqrt{2} s i n 45 °$ .

查看试题解析
18. 面对新冠疫情，宁波教育人同心战“疫”.因有不少师生居家健康监测，无法到校工作、学习，各校师生通过“云端”相连，停课不停教，停课不停学.某校在疫情期间的教学方式主要包括直播授课、录播授课、自主学习、在线答疑四种形式.为了了解学生的需求，该校随机对部分学生进行了“你对哪种教学方式最感兴趣”的调查（每人只选其中的一种），并根据调查结果绘制成如下图所示的统计图.

(1)、本次调查的人数是人；

(2)、请补全条形统计图；

(3)、明明和强强参加了此次调查，均选择了其中一种教学方式，请用树状图或列表表示所有可能的情况，并求明明和强强选择同一种教学方式的概率.

查看试题解析
19. 如图，在平面直角坐标系xOy中，一次函数y=x的图象与二次函数y=-x2+bx（b为常数）的图象相交于O，A两点，点A坐标为（3，m）.

(1)、求m的值以及二次函数的表达式；

(2)、若点P为抛物线的顶点，连结OP，AP，求△POA的面积.

查看试题解析
20. 某小区门口安装了汽车出入道闸.道闸关闭时，如图1，四边形ABCD为矩形，AB长3米，AD长1米，点D距地面为0.2米.道闸打开的过程中，边AD固定，连杆AB，CD分别绕点A，D转动，且边BC始终与边AD平行.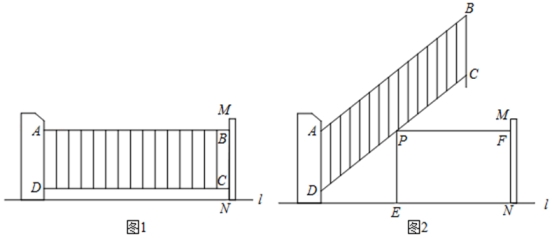

(1)、如图2，当道闸打开至∠ADC＝45°时，边CD上一点P到地面的距离PE为1.2米，求点P到MN的距离PF的长.

(2)、一辆轿车过道闸，已知轿车宽1.8米，高1.6米.当道闸打开至∠ADC＝36°时，轿车能否驶入小区？请说明理由.（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73）

查看试题解析
21. 如图1，AB是⊙O的直径，点C是⊙O上异于点A，B的一点，连接AC，BC，并延长BA至点E，使得∠ECA=∠B.

(1)、求证：CE是⊙O的切线；

(2)、如图2，若∠B=30°，请写出三个你认为正确的结论（注：不另外添加辅助线）.

查看试题解析
22. 某琴行销售一种笛子，每支进价为56元.当售价每支为80元时，月平均销售量为60支.为了倡导、弘扬艺术，琴行对该型号的笛子作降价销售（在不亏本的前提下）.经市场调查表明，当每支笛子的售价每降低1元时，月平均销售量将增加3支.

(1)、若设销售单价为 $x$ 元/支，则销售量为支（用含 $x$ 的代数式表示）；

(2)、求月平均销售利润 $y$ （单位：元）关于销售单价 $x$ （单位：元/支）的函数表达式；

(3)、当销售单价定为每支多少元时，所得月平均利润最大？

查看试题解析
23. 利用网格图，可以仅用无刻度的直尺来完成几何作图.（注：以下点 $A 、 B 、 M 、 N$ 均在格点上.）
【赏析】

(1)、提出问题：下列图是由边长为1的小正方形构成的网格图.在网格图1中的线段 $A B$ 上，求作一点 $P$ ，使得 $B P = 2 A P$ .

(2)、观察欣赏：在图2中， $A M = 2 ， B N = 4$ ，且 $A M ∥ B N$ .连结 $M N$ 交 $A B$ 于点 $P$ ，点 $P$ 即为所求作之点，此时 $B P = 2 A P$ .
求证：在图3中，点 $P$ 也为所求作之点，即 $B P = 2 A P$ .

(3)、【尝试】
作图：下列图是由边长为1的小正六边形构成的网格图.请在线段 $A B$ 上求作点 $P$ .
①在图4中，过格点 $M$ 作线段 $M N$ 与 $A B$ 交于点 $P$ ，使得 $A P = \frac{2}{5} B P$ .

②在图5中，求作点 $P$ ，使得 $A P = \frac{2}{5} B P$ .（要求：方法与①有别，不写作法但保留作图痕迹）

查看试题解析
24. 如图，等腰△ABC内接于⊙O，AB=AC，连结OC，过点B作AC的垂线，交⊙O于点D，交OC于点M，交AC于点E，连结AD.

(1)、若∠D=α，请用含α的代数式表示∠OCA；

(2)、如图1.
①求证：CE²=EM•EB；
②若BM=3，DM=2，求tan∠BAC的值.

(3)、如图2，连结CD，若 $x = \frac{D M}{B M} ， y = \frac{S_{四边形 A B C D}}{S_{△ B M C}}$ ，求y关于x的函数表达式.

查看试题解析

抽检件数	5	50	100	500	1000	2000	3000	5000
不合格件数	0	1	2	9	21	40	60	100
不合格频率	0	$0.02$	$0.02$	$0.018$	$0.021$	$0.02$	$0.02$	$0.02$