浙江省宁波市奉化区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-22 类型：期末考试

进入出卷网下载

一、单选题

1. 若二次函数 $y = a x^{2}$ 的图象经过点 $(- 2 ， - 4)$ ，则a的值为（）

A、-2 B、2 C、-1 D、1

查看试题解析
2. “a是实数，|a|≥0”这一事件是（）

A、必然事件 B、不确定事件 C、不可能事件 D、随机事件

查看试题解析
3. 正八边形每个内角度数为（）

A、120° B、135° C、150° D、160°

查看试题解析
4. 一个不透明的盒子里装有a个除颜色外完全相同的球，其中有6个白球，每次将球充分搅匀后，任意摸出1个球记下颜色然后再放回盒子里，通过如此大量重复试验，发现摸到白球的频率稳定在0.4左右，则a的值约为（）

A、10 B、12 C、15 D、18

查看试题解析
5. 由抛物线 $y = x^{2}$ 平移得到抛物线 $y = {(x + 4)}^{2}$ 则下列平移方式可行的是（）

A、向左平移4个单位长度 B、向右平移4个单位长度 C、向下平移4个单位长度 D、向上平移4个单位长度

查看试题解析
6. 在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $s i n A = \frac{3}{5}$ ，则 $t a n A =$ （）

A、 $\frac{4}{5}$ B、 $\frac{3}{4}$ C、 $\frac{4}{3}$ D、 $\frac{5}{4}$

查看试题解析
7. 已知 $A (- 1 ， y_{1})$ ， $B (- 3 ， y_{2})$ ， $C (4 ， y_{3})$ 在二次函数 $y = - x^{2} - 6 x + c$ 的图象上， $y_{1}$ ， $y_{2}$ ， $y_{3}$ 则的大小关系是（）

A、 $y_{3} > y_{1} > y_{2}$ B、 $y_{2} > y_{1} > y_{3}$ C、 $y_{1} > y_{2} > y_{3}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析
8. 把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知 $E F = C D = 6$ cm，则球的半径为（）

A、3cm B、 $\frac{13}{4}$ cm C、 $\frac{15}{4}$ cm D、 $\frac{17}{4}$ cm

查看试题解析
9. 如图，由五个边长都是1的正方形纸片拼接而成的，过点 $A_{1}$ 的线段分别与 $B C_{1}$ ， BE交于点M，N，则 $\frac{1}{M B} + \frac{1}{N B} =$ （）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\sqrt{5}$ C、 $\frac{\sqrt{2}}{2}$ D、1

查看试题解析
10. 如图，矩形ABCD被分割成4个小矩形，其中矩形AEPH~矩形HDFP~矩形PEBG， $A E > A H$ ， AC交HG，EF于点M，Q，若要求 $△ A P Q$ 的而积，需知道下列哪两个图形的面积之差（）

A、矩形AEPH和矩形PEBG B、矩形HDFP和矩形AEPH C、矩形HDFP和矩形PEBG D、矩形HDFP和矩形PGCF

查看试题解析

二、填空题

11. 若 $\frac{a}{2} = \frac{b}{3}$ 则 $\frac{a - b}{a + b} =$ .

查看试题解析
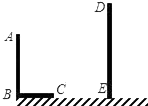
12. 在同一平面上， $⊙ O$ 外有一点P到圆上的最大距离是8cm，最小距离为2cm，则 $⊙ O$ 的半径为cm.

查看试题解析
13. 如图，AB和DE是直立在地面上的两根立柱，AB=5米，某一时刻AB在阳光下的投影BC=3米，在测量AB的投影时，同时测量出DE在阳光下的投影长为6米，则DE的长为

查看试题解析
14. 如图，从一块直径为2cm的圆形铁皮上剪出一圆心角为90°的扇形，则此扇形的面积为cm² ．

查看试题解析
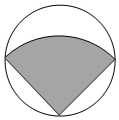15. 如图，点A在半径为5的 $⊙ O$ 内， $O A = \sqrt{3}$ ， P为 $⊙ O$ 上一动点，当 $∠ O P A$ 取最大值时，PA的长等于.

查看试题解析
16. 已知过点 $B (4 ， 1)$ 的抛物线 $y = \frac{1}{2} x^{2} - \frac{5}{2} x + c$ 与坐标轴交于点A，C如图所示，连结AC，BC，AB，第一象限内有一动点M在抛物线上运动，过点M作 $A M ⊥ M P$ 交y轴于点P，当点P在点A上方，且 $△ A M P$ 与 $△ A B C$ 相似时，点M的坐标为.

查看试题解析

三、解答题

17. $2 s i n 30 ° - t a n 60 ° + c o s 30 ° - t a n^{2} 45 °$

查看试题解析
18. 在 $4 \times 4$ 的方格纸中， $△ A B C$ 的三个顶点都在格点上.

(1)、在图1中画出与 $△ A B C$ 相似（不全等）且以AC为公共边的格点三角形（画出一个即可）；

(2)、将图2中的 $△ A B C$ 绕着点C按顺时针方向旋转90°，画出经旋转后的三角形.

查看试题解析
19. 芳芳家有一种伸缩挂衣架（如图1），伸缩挂衣架中有3个菱形组成，每个菱形边长为10cm.伸缩挂衣架打开时，每个菱形的锐角度数为60°（如图2）；伸缩挂衣架收拢时，每个菱形的锐角度数从60°缩小为10°（如图3）.问：伸缩挂衣架从打开到收拢共缩短了多少cm?（结果精确到1cm，参考数据： $s i n 5 ° \approx 0.0872$ ， $c o s 5 ° \approx 0.9962$ ， $s i n 10 ° \approx 0.1736$ ， $c o s 10 ° \approx 0.9848$ ）.

查看试题解析
20. 随着课后服务的全面展开，某校组织了丰富多彩的社团活动.炯炯和露露分别打算从以下四个社团：A.快乐足球，B.数学历史，C.文学欣赏，D.棋艺鉴赏中，选择一个社团参加.

(1)、炯炯选择数学历史的概率为.

(2)、用画树状图或列表的方法求炯炯和露露选择同一个社团的概率.

查看试题解析
21. 如图，AB是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点E， $∠ C D B = 30 °$ ， $C D = 2 \sqrt{3}$

(1)、求直径AB的长；

(2)、求阴影部分图形的面积.

查看试题解析
22. “互联网+”时代，网上购物备受消费者青睐.某网店专售一款休闲裤，其成本为每条60元，当售价为每条80元时，每月可销售100条.为了吸引更多顾客，该网店采取降价措施.据市场调查反映：销售单价每降1元，则每月可多销售10条.设每条裤子的售价为x元（x为正整数），每月的销售量为y条.

(1)、直接写出y与x的函数关系式；

(2)、设该网店每月获得的利润为w元，当销售单价为多少元时，每月获得的利润最大，最大利润是多少?

(3)、该网店店主热心公益事业，决定每月从利润中捐出500元资助贫困学生.为了保证捐款后每月利润不低于1590元，且让消费者得到最大的实惠，该如何确定休闲裤的销售单价?

查看试题解析
23. 如图，抛物线 $y = \frac{1}{2} x^{2} - \frac{3}{2} x - 2$ 与x轴交于点A，B，与y轴交于点C.点P是线段BC上的动点（点P不与点B，C重合），连接并延长AP交抛物线于另一点Q，连接CQ，BQ，设点Q的横坐标为x.

(1)、①写出点A，B，C的坐标：A（），B（），C（）；②求证： $△ A B C$ 是直角三角形；

(2)、记 $△ B C Q$ 的面积为S，求S关于x的函数表达式；

(3)、在点P的运动过程中， $\frac{P Q}{A P}$ 是否存在最大值？若存在，求出 $\frac{P Q}{A P}$ 的最大值及此时点Q的坐标；若不存在，请说明理由.

查看试题解析
24. 阅读材料，某个学习小组成员发现：在等腰 $△ A B C$ 中，AD平分 $∠ B A C$ ， ∵ $A B = A C$ ， $B D = C D$ ， ∴ $\frac{A B}{A C} = \frac{B D}{C D}$ ，他们猜想：在任意 $△ A B C$ 中，一个内角角平分线分对边所成的两条线段与这个内角的两边对应成比例.
【证明猜想】如图1所示，在 $△ A B C$ 中，AD平分 $∠ B A C$ ，求证： $\frac{A B}{A C} = \frac{B D}{C D}$ .
丹丹认为，可以通过构造相似三角形的方法来证明；
思思认为，可以通过比较 $△ A B D$ 和 $△ A C D$ 面积的角度来证明.

(1)、请你从上面的方法中选择一种进行证明.

(2)、【尝试应用】如图2， $⊙ O$ 是 $R t △ A B C$ 的外接圆，点E是 $⊙ O$ 上一点（与B不重合，且 $A B = A E$ ，连结 $A E$ ，并延长AE，BC交于点D，H为AE的中点，连结BH交AC于点G，求 $\frac{H G}{G B}$ 的值.

(3)、【拓展提高】如图3，在（2）的条件下，延长 $B H$ 交 $⊙ O$ 于点F，若 $B E = E F$ ， $G H = x$ ，求 $⊙ O$ 的直径（用x的代数式表示）.

查看试题解析