浙江省金华市义乌市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-22 类型:期末考试
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列几何体中,俯视图是矩形的是( )A、
 B、
B、 C、
C、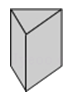 D、
D、 3. 事件“任意抛掷一枚骰子,点数为3的面朝上”是( )A、确定事件 B、随机事件 C、必然事件 D、不可能事件4. 下列条件中,能确定一个圆的是( )A、以点为圆心 B、以长为半径 C、以点为圆心,长为半径 D、经过已知点5. 下列图形中,是相似形的是( )A、所有平行四边形 B、所有矩形 C、所有菱形 D、所有正方形6. 用配方法将二次函数y=x2﹣8x﹣9化为y=a(x﹣h)2+k的形式为( )A、y=(x﹣4)2+7 B、y=(x+4)2+7 C、y=(x﹣4)2﹣25 D、y=(x+4)2﹣257. 图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形 . 若 , , 则的值为( )
3. 事件“任意抛掷一枚骰子,点数为3的面朝上”是( )A、确定事件 B、随机事件 C、必然事件 D、不可能事件4. 下列条件中,能确定一个圆的是( )A、以点为圆心 B、以长为半径 C、以点为圆心,长为半径 D、经过已知点5. 下列图形中,是相似形的是( )A、所有平行四边形 B、所有矩形 C、所有菱形 D、所有正方形6. 用配方法将二次函数y=x2﹣8x﹣9化为y=a(x﹣h)2+k的形式为( )A、y=(x﹣4)2+7 B、y=(x+4)2+7 C、y=(x﹣4)2﹣25 D、y=(x+4)2﹣257. 图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形 . 若 , , 则的值为( )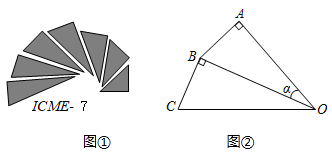 A、 B、 C、 D、8. 如图,在由边长相同的7个正六边形组成的网格中,点A,B在格点上.再选择一个格点C,使△ABC是以AB为腰的等腰三角形,符合点C条件的格点个数是( )
A、 B、 C、 D、8. 如图,在由边长相同的7个正六边形组成的网格中,点A,B在格点上.再选择一个格点C,使△ABC是以AB为腰的等腰三角形,符合点C条件的格点个数是( ) A、1 B、2 C、3 D、49. 如图,在平行四边形ABCD中, , , 以顶点C为圆心,BC为半径作圆,则AD边所在直线与的位置关系是( )
A、1 B、2 C、3 D、49. 如图,在平行四边形ABCD中, , , 以顶点C为圆心,BC为半径作圆,则AD边所在直线与的位置关系是( )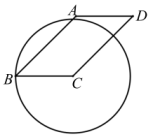 A、相交 B、相切 C、相离 D、以上三种都有可能10. 已知二次函数(h为常数),当时,函数y的最大值为 , 则h的值为( )A、1或3 B、4或6 C、3或6 D、1或6
A、相交 B、相切 C、相离 D、以上三种都有可能10. 已知二次函数(h为常数),当时,函数y的最大值为 , 则h的值为( )A、1或3 B、4或6 C、3或6 D、1或6二、填空题
-
11. 已知点P在半径为r的内,.请写一个满足条件的r的值.12. 比较与的大小,结果为:.13. 某一时刻,测得身高1.6的同学在阳光下的影长为2.8 , 同时测得教学楼在阳光下的影长为25.2 , 则教学楼的高为.14. 如图,是的直径,点是上一点, , , 则阴影部分的面积为.
 15. 如图,在一块边长为的正方形纸板ABCD,做成如图1所示的一套七巧板(点O为正方形纸板对角线的交点),点E、F分别为AD、CD的中点.若将图1中的七巧板拼出如图2所示的“鱼形”,则“鱼尾”MN的长为.
15. 如图,在一块边长为的正方形纸板ABCD,做成如图1所示的一套七巧板(点O为正方形纸板对角线的交点),点E、F分别为AD、CD的中点.若将图1中的七巧板拼出如图2所示的“鱼形”,则“鱼尾”MN的长为. 16. 图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成. 图2是其侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂). 已知基座高度MN为0.5米,主臂MP长为米,主臂伸展角α的范围是:0°<α≤60°,伸展臂伸展角β的范围是:45°≤β≤135°.当α=45°时(如图3),伸展臂PQ恰好垂直并接触地面.
16. 图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成. 图2是其侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂). 已知基座高度MN为0.5米,主臂MP长为米,主臂伸展角α的范围是:0°<α≤60°,伸展臂伸展角β的范围是:45°≤β≤135°.当α=45°时(如图3),伸展臂PQ恰好垂直并接触地面. (1)、伸展臂PQ长为米;(2)、挖掘机能挖的最远处距点N的距离为米.
(1)、伸展臂PQ长为米;(2)、挖掘机能挖的最远处距点N的距离为米.三、解答题
-
17. 已知 , 求的值.18. 从长为9,6,5,4的四根木条中任取三根.(1)、请直接写出不同的取法有几种?分别列举出来.(2)、求能组成三角形的概率.19. 如图是由小正方形组成的6×6网格,的三个顶点A、B、C都在格点上.在给定的网格中,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹,不写画法.
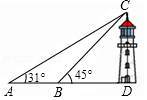
 (1)、在图1中作的中线AD;(2)、在图2中作的高线BE;(3)、在图3中AC边上确定点F,使得.20. 如图,海面上一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,再向东继续航行30m到达B处,测得该灯塔的最高点C的仰角为45°,根据测得的数据,计算这座灯塔的高度CD(结果取整数).
(1)、在图1中作的中线AD;(2)、在图2中作的高线BE;(3)、在图3中AC边上确定点F,使得.20. 如图,海面上一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,再向东继续航行30m到达B处,测得该灯塔的最高点C的仰角为45°,根据测得的数据,计算这座灯塔的高度CD(结果取整数).参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60.
 21. 如图,在中, , 点O在斜边AB上,以O为圆心,OA为半径的圆切BC于点D,交AB、AC分别于点E、F,连结OD.
21. 如图,在中, , 点O在斜边AB上,以O为圆心,OA为半径的圆切BC于点D,交AB、AC分别于点E、F,连结OD. (1)、求证:点D为的中点;(2)、若 , , 求的直径AE的长.22. 种植户王大伯的大棚种植了许多优质草莓.因受疫情影响,多地封村村路,无法正常销售,于是就进行了网上预订送货销售活动.在销售的30天中,第一天卖出20kg,为了扩大销售,采取了降价措施,以后每天比前一天多卖出4kg.第x天的售价为y元/kg,y关于x的解析式为.第12天的售价为32元/kg,第26天的售价为25元/kg.已知种植销售草莓的成本是18元/kg,设第x天的销售量为p kg,利润为W元(利润=销售收入-成本).(1)、k= , b=;(2)、请写出p关于x的函数关系式: ;(3)、求销售草莓第几天,当天销售利润最大?最大利润是多少元?23. 如图1,直线与x,y轴分别相交于A、B两点.将绕点O逆时针旋转90°得到 , 过点A,B,D的抛物线P叫做直线l的关联抛物线,直线l叫做P的关联直线.
(1)、求证:点D为的中点;(2)、若 , , 求的直径AE的长.22. 种植户王大伯的大棚种植了许多优质草莓.因受疫情影响,多地封村村路,无法正常销售,于是就进行了网上预订送货销售活动.在销售的30天中,第一天卖出20kg,为了扩大销售,采取了降价措施,以后每天比前一天多卖出4kg.第x天的售价为y元/kg,y关于x的解析式为.第12天的售价为32元/kg,第26天的售价为25元/kg.已知种植销售草莓的成本是18元/kg,设第x天的销售量为p kg,利润为W元(利润=销售收入-成本).(1)、k= , b=;(2)、请写出p关于x的函数关系式: ;(3)、求销售草莓第几天,当天销售利润最大?最大利润是多少元?23. 如图1,直线与x,y轴分别相交于A、B两点.将绕点O逆时针旋转90°得到 , 过点A,B,D的抛物线P叫做直线l的关联抛物线,直线l叫做P的关联直线. (1)、若直线 , 则抛物线P表示的函数解析式为 , 若抛物线 , 则直线l表示的函数解析式为;(2)、如图2,若直线 , G为AB中点,H为CD的中点,连接GH,取GH中点M,连接OM,已知.求直线l的关联抛物线P表示的函数解析式;(3)、若将某直线的关联抛物线向右平移个单位得到抛物线 , 则a、m、n应满足的关系式为.24. 如图1,在矩形ABCD中, , , 点E在AB边上,且.点F是BC边上的动点.将沿EF折叠得到.直线GF与直线AB的交点为H.
(1)、若直线 , 则抛物线P表示的函数解析式为 , 若抛物线 , 则直线l表示的函数解析式为;(2)、如图2,若直线 , G为AB中点,H为CD的中点,连接GH,取GH中点M,连接OM,已知.求直线l的关联抛物线P表示的函数解析式;(3)、若将某直线的关联抛物线向右平移个单位得到抛物线 , 则a、m、n应满足的关系式为.24. 如图1,在矩形ABCD中, , , 点E在AB边上,且.点F是BC边上的动点.将沿EF折叠得到.直线GF与直线AB的交点为H. (1)、如图2,点F与点C重合时,求与的面积比;(2)、如图3,当H在点A的上方,且满足三角形HEF是等腰三角形时,求线段EH的长.(3)、在点F的运动过程中,以E、G、H为顶点的三角形能否与以B、C、D为顶点的三角形相似?若能,求BF的长;若不存在,请说明理由.
(1)、如图2,点F与点C重合时,求与的面积比;(2)、如图3,当H在点A的上方,且满足三角形HEF是等腰三角形时,求线段EH的长.(3)、在点F的运动过程中,以E、G、H为顶点的三角形能否与以B、C、D为顶点的三角形相似?若能,求BF的长;若不存在,请说明理由.