浙江省金华市武义县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列成语中，表示不可能事件的是（）

A、水中捞月 B、守株待兔 C、水涨船高 D、水滴石穿

查看试题解析
2. 已知 $\frac{x}{y} = \frac{2}{3}$ ，则下列等式中正确的是（）

A、 $2 x = 3 y$ B、 $\frac{x + y}{y} = \frac{5}{2}$ C、 $\frac{y}{x} = \frac{3}{2}$ D、 $x = 2$ ， $y = 3$

查看试题解析
3. 如图，在 $△$ AOB中，∠AOB＝30°，将 $△$ AOB绕点O逆时针旋转70°得到 $△$ COD，则∠BOC的度数是（）

A、70° B、40° C、35° D、30°

查看试题解析
4. 如图，点A，B，C，D是⊙O上的四个点，且 $A B = C D$ ， OE⊥AB，OF⊥CD，则下列结论错误的是（）

A、 $\overset{⌢}{A B} = \overset{⌢}{C D}$ B、 $O E = O F$ C、 $∠ A O B = ∠ C O D$ D、 $\overset{⌢}{A C} = \overset{⌢}{B C}$

查看试题解析
5. 函数 $y = - x^{2} + 3$ 与 $y = - x^{2} - 2$ 的图象的不同之处是（）

A、顶点 B、对称轴 C、开口方向 D、形状

查看试题解析
6. 如图，小明在8：30测得某树的影长为16m，13：00时又测得该树的影长为4m，若两次日照的光线互相垂直，则这棵树的高度为（）

A、10m B、8m C、6m D、4m

查看试题解析
7. 下列说法中，不正确的是（）

A、全等图形一定是相似图形 B、直角边长分别是6，4和4.5，3的两个直角三角形相似 C、任意两个矩形都相似 D、三角形的重心分每一条中线成1：2的两条线段

查看试题解析
8. 飞机着陆后滑行的距离s（单位：米）关于滑行时间t（单位：秒）的函数表达式为 $s = a t^{2} + b t$ ，当滑行时间为10秒时，滑行距离为450米；当滑行时间为20秒时，滑行距离为600米，则飞机的最大滑行距离为（）

A、600米 B、800米 C、1000米 D、1200米

查看试题解析
9. 如图，在Rt $△$ ABC中，∠CAB＝36°，斜边AC与量角器的直径重合（A点的刻度为0），将射线BF绕着点B转动，与量角器的外圆弧交于点D，与AC交于点E，若 $△$ ABE是等腰三角形，则点D在量角器上对应的刻度为（）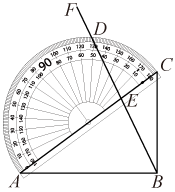

A、72° B、144° C、36°或72° D、72°或144°

查看试题解析
10. 已知抛物线 $y = a x^{2} + b x + c$ （a，b，c都是常数，且 $a \neq 0$ ）开口向上且过点 $A (- 1 ， 0)$ ， $B (m ， 0)$ （ $1 < m < 2$ ），小明得出下列结论：① $b > 0$ ；②若 $(- 1 ， y_{1})$ 和 $(1 ， y_{2})$ 都在抛物线上，则 $y_{1} > y_{2}$ ；③ $2 a + c > 0$ ；④若方程 $a (x - m) (x + 1) + 4 = 0$ 没有实数根，则 $b^{2} - 4 a c < 16 a$ .其中正确结论的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

二、解答题

11. 已知抛物线 $y = x^{2} + 4 x + 3$ .

(1)、求抛物线与x轴的交点坐标.

(2)、求抛物线的顶点坐标.

查看试题解析
12. 如图，在直角坐标系中， $△$ ABC各顶点的坐标为 $A (- 1 ， 1)$ ， B（2，3），C（0，3）.

(1)、以坐标原点O为位似中心，在x轴上方作与 $△$ ABC的位似比为2的位似图形 $△ A^{'} B^{'} C^{'}$ .

(2)、顶点 $A^{'}$ 的坐标为， $△ A^{'} B^{'} C^{'}$ 与 $△$ ABC的面积之比为.

查看试题解析
13. 如图，在四边形ABCD中，AC，BD交于点F.点E在BD上，且 $∠ B A E = ∠ C A D$ ， $\frac{A B}{A E} = \frac{A C}{A D}$ .

(1)、求证： $△ A B C ∽ △ A E D$ .

(2)、若 $∠ B A E = 20 °$ ，求∠CBD的度数.

查看试题解析
14. 在一个不透明的口袋里装有若干个相同的红球，为了估计袋中红球的数量，九（2）班学生在数学实验室分组做摸球实验：每组先将15个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表：
摸球的次数s
150
300
600
900
1200
1500
摸到红球的频数n
63
123
247
365
484
603
摸到红球的频率 $\frac{n}{s}$
0.420
0.410
0.412
0.406
0.403
a

(1)、a＝.

(2)、请估计：当次数s很大时，摸到红球的频率将会接近（精确到0.01）；请推测：摸到红球的概率是（精确到0.1）.

(3)、求口袋中红球的数量.

查看试题解析
15. 小林大学毕业后回家乡创业，第一期培植盆景与花卉各100盆，据售后统计，盆景平均每盆利润是320元，花卉平均每盆利润是35元，经市场调研，得出如下结论：①盆景每增加1盆，平均每盆利润减少2元.②花卉平均每盆的利润始终不变.小林计划第二期培植盆景与花卉共200盆，设培植的盆景比第一期增加x盆，第二期盆景与花卉售完后的利润分别为 $W_{1}$ ， $W_{2}$ （单位：元）.

(1)、用含x的代数式分别表示 $W_{1}$ ， $W_{2}$ .

(2)、当x取何值时，第二期培植的盆景与花卉售出后获得的总利润W最大？最大利润是多少？

查看试题解析
16. 金华境内峰峦叠嶂，公路隧道众多，如图1所示的圆弧形混凝土管片是构成圆形隧道的重要部件.管片的横截面（阴影部分）如图2所示，是同心圆环的一部分，左右两边沿的延长线交于圆心，甲、乙、丙三个小组分别采用三种不同的方法，测算三片不同大小的混凝土管片的外圆弧半径.

(1)、如图2，BA，CD的延长线交于圆心O，若甲组测得AB＝0.6m，AD＝3m，BC＝4m，求OB的长.

(2)、如图3，ED，FC的延长线交于圆心H，若乙组测得DE＝0.8m， $\overset{⌢}{C D} = 12 m$ ， $\overset{⌢}{E F} = 15 m$ ，求EH的长.

(3)、如图4，有一混凝土管片放置在水平地面上，底部用两个完全相同的长方体木块固定，管片与地面的接触点L为 $\overset{⌢}{M P}$ 的中点，若丙组测得MN＝PQ＝0.5m，NL＝LQ＝2m，求该混凝土管片的外圆弧半径.

查看试题解析

17. 某“数学兴趣小组”根据学习函数的经验，对函数

y = - (x - 1) (| x | - 3)

的图象和性质进行了探究，探究过程如下，请补充完整：

(1)、自变量x的取值范围是；x与y的几组对应值如表，其中m＝.

x	…	$- 4$	$- 3$	$- 2$	$- 1$	0	1	2	3	4	…
y	…	5	0	$- 3$	m	$- 3$	0	1	0	$- 3$	…

(2)、如图，在直角坐标系中画出了函数

y = - (x - 1) (| x | - 3)

的部分图象，用描点法将这个图象补画完整.

(3)、结合函数图象，解决下列问题：

①解不等式： $- 3 \leq - (x - 1) (| x | - 3) \leq - 1$ .

②若过定点的直线 $y = t x - 2 t + 2$ 与函数 $y = - (x - 1) (| x | - 3) (- 3 \leq x \leq 4)$ 的图象只有一个横坐标不等于2的交点，求出t的取值范围.

查看试题解析

18. 如图1，已知AB为半圆O的直径，AB＝2，线段AI⊥AB，延长AB至点G，使BG＝AB，以点B为圆心，线段AG为直径作半圆B，点D是半圆B上一点，过点D作DF⊥AI于点F，连结AD，BD，其中AD交半圆O于点E.连接EF.

(1)、求证：AE＝DE.

(2)、设 $E F = x$ ， $D F = y$ ，求y关于x的函数表达式及自变量x的取值范围.

(3)、如图2，以BG为直径作半圆 $O^{'}$ ， BD交半圆O或半圆 $O^{'}$ 于点J，连结FB交AD于点K，连结KJ，当点K将线段FB分为2：3两部分时，求 $△$ DFK与 $△$ BJK的面积之差.

查看试题解析

三、填空题

19. 圆是轴对称图形，它的对称轴有条.

查看试题解析
20. 点C是线段AB的黄金分割点， $A C > B C$ .若 $A B = 2 c m$ ，则 $A C =$ cm.

查看试题解析
21. 现有四张大小形状一样且背面完全相同的卡片，正面分别写有汉字“爱”“我”“中”“华”.把它们背面朝上，从中任抽2张，其正面上的文字恰好可以组成“中华”字样的概率为.

查看试题解析
22. 如图，某拱桥桥洞的形状是抛物线，若取水平方向为x轴，拱桥的拱点O为原点建立直角坐标系，它可以近似地用函数 $y = - \frac{1}{8} x^{2}$ 表示（单位：m）．已知目前桥下水面宽4m，若水位下降1.5m，则水面宽为m．

查看试题解析
23. 如图，将正方形ABCD的边AB，BC绕着点A逆时针旋转一定角度，得到线段 $A B^{'}$ ， $B^{^{'}} C^{^{'}}$ ，连接 $A C^{'}$ 交CD于点E，连接 $B B^{'}$ ， $C C^{'}$ ，若 $△ A B B^{'} ∽ △ C E C^{'}$ ，则 $∠ A B B^{'} =$ .

查看试题解析
24. 某校航天社团模拟火星探测器的发射过程，如图，地球，火星的运行轨道抽象成以太阳O为圆心的圆，探测器从地球到火星的转移轨道则抽象成以 $O^{'}$ 为圆心，AC为直径的半圆.点O在AC上，点A，B分别代表探测器从地球发射时地球和火星的位置，火星沿 $\overset{⌢}{B C}$ 运行，与探测器同时抵达C点，已知 $∠ A O B = 44 °$ ，火星的公转周期（绕太阳逆时针转动一周所用时间）为687天，地球与火星的轨道半径OA，OC分别为1A.U.和1.5A.U.（A.U.为天文单位）.

(1)、探测器从发射到抵达火星需要天（精确到个位）.

(2)、当探测器运行到点T时，太阳爆发活动向探测器方向抛射速度为 $\frac{1}{30} A . U . / h$ 的体积巨大的“等离子体云”，此时TC恰好等于点 $O^{'}$ 到TC中点的距离，则最快h后，探测器会受到“等离子体云”的干扰（短时间内探测器的运行路程可忽略不计）.

查看试题解析

摸球的次数s	150	300	600	900	1200	1500
摸到红球的频数n	63	123	247	365	484	603
摸到红球的频率 $\frac{n}{s}$	0.420	0.410	0.412	0.406	0.403	a