浙江省嘉兴市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-11-22 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $\frac{a}{b} = \frac{3}{7}$ ，则 $\frac{a + b}{b}$ 的值（）

A、 $\frac{10}{7}$ B、 $\frac{3}{7}$ C、 $\frac{3}{4}$ D、 $\frac{7}{10}$

查看试题解析
2. 如图，AB是⊙O的直径，点C在圆上，若 $∠ A B C = 70 °$ ，则 $∠ B A C$ 的度数为（）

A、70° B、60° C、40° D、20°

查看试题解析
3. 下列事件中，属于必然事件的是（）

A、在地面上向空中抛一石头，石头终将下落 B、嘉兴明天最高气温是15℃ C、射击运动员射击一次，命中10环 D、一匹马奔跑的速度是70米/秒

查看试题解析
4. 若⊙O的半径为6，点P在⊙O内，则OP的长可能是（）

A、5 B、6 C、7 D、8

查看试题解析
5. 如图，在 $△ A B C$ 中，D，E分别是边AB，AC上的点， $D E ∥ B C$ ，若 $S_{△ A D E} ：$ S_四_边_形DBCE=1：8，则 $\frac{D E}{B C}$ 的值为（）

A、 $1 ： 9$ B、 $1 ： 3$ C、 $1 ： 2 \sqrt{2}$ D、 $1 ： 8$

查看试题解析
6. 将二次函数y=(x﹣1)²+2的图象向上平移3个单位长度，得到的拋物线相应的函数表达式为（）

A、y=(x+2)²﹣2 B、y=(x﹣4)²+2 C、y=(x﹣1)²﹣1 D、y=(x﹣1)²+5

查看试题解析
7. 如图，⊙O的直径AB=12，CD是⊙O的弦，CD⊥AB，垂足为P，且BP=2，则CD的长为（）

A、 $2 \sqrt{5}$ B、 $4 \sqrt{2}$ C、 $4 \sqrt{5}$ D、 $8 \sqrt{2}$

查看试题解析
8. 如图，在平面直角坐标系中，已知点A（2，4），B（4，1），以原点O为位似中心，将△OAB缩小为原来的 $\frac{1}{2}$ ，则点A的对应点A的坐标是（）

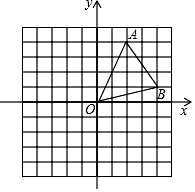A、（2， $\frac{1}{2}$ ） B、（1，2） C、（4，8）或（﹣4，﹣8） D、（1，2）或（﹣1，﹣2）

查看试题解析
9. 如图，在 $△ A B C$ 中， $C A = C B$ ， $∠ A C B = 9 0^{∘}$ ， $A B = 2$ ，点 $D$ 为 $A B$ 的中点，以点 $D$ 为圆心作圆心角为 $9 0^{∘}$ 的扇形 $D E F$ ，点 $C$ 恰在弧 $E F$ 上，则图中阴影部分的面积为（）

A、 $\frac{π}{2} + \frac{1}{2}$ B、 $π - \frac{1}{4}$ C、 $\frac{π}{4} + \frac{1}{2}$ D、 $\frac{π}{4} - \frac{1}{2}$

查看试题解析
10. 已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 交x轴于点 $A (1 ， 0)$ ， $B (3 ， 0)$ . $P_{1} (x_{1} ， y_{1})$ ， $P_{2} (x_{2} ， y_{2})$ 是抛物线上两个点.若 $| x_{1} - 2 | > | x_{2} - 2 | > 1$ ，则下列结论一定正确的是（）

A、 $y_{1} < y_{2}$ B、 $y_{1} > y_{2}$ C、 $| y_{1} | < | y_{2} |$ D、 $| y_{1} | > | y_{2} |$

查看试题解析

二、填空题

11. 正五边形的每一个内角都等于．

查看试题解析
12. 若抛物线 $y = x^{2} - x + k$ 与x轴只有一个交点，则k的值为.

查看试题解析
13. 如图，C是⊙O上一点，若 $∠ A C B = 24 °$ ，则 $∠ A O B$ 的度数是.

查看试题解析
14. 如图，点D在△ABC的边AC上，若要使△ABD与△ACB相似，可添加的一个条件是（只需写出一个）．

查看试题解析
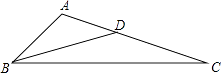15. 已知点P是线段 $A B$ 的黄金分割点， $P A > P B ， A B = 4 c m$ ，那么 $P A =$ $c m$ ．

查看试题解析
16. 随机抽检一批衬衣的合格情况，得到如下的频数表.
抽取件数（件）
100
150
200
500
800
1000
合格频数
900
141
189
474
760
950
合格频率
0.90
0.94
0.945
0.948
0.95
0.95
则出售这批衬衣2000件，估计次品大约有件.

查看试题解析
17. 如图，矩形ABCD∽矩形BCEF，若AB=8，BC=6，则CE的值为.

查看试题解析
18. 如图，在直角三角形纸片ABC中， $∠ A C B = 90 °$ ， $A B = 5$ ， $A C = 3$ ， D是BC上一动点，连结AD，将 $△ A C D$ 沿AD折叠，点C落在点E处，连结DE交AB于点F，当 $∠ B D E = 90 °$ 时，DF的长为.

查看试题解析
19. 甲、乙两人研究二次函数 $y = a x^{2} - 4 a x + 3 (a \neq 0)$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ ，甲说：“二次函数图象一定过第一象限的一个定点.”乙说：“二次函数图象的顶点及这个定点都在该反比例函数图象上.”若甲、乙两人的描述正确，则a的值为.

查看试题解析
20. 如图，⊙O的直径 $A B = 2$ ， C为⊙O上动点，连结CB，将CB绕点C逆时针旋转90°得到CD，连结OD，则OD的最大值为.

查看试题解析

三、解答题

21. 已知二次函数y=x²-2x+m的图象过点A（3，0）.

(1)、求m的值；

(2)、自变量x在什么范围时，y随x的增大而增大？

查看试题解析
22. “红船精神”是建党100周年学习的重要精神，现将质地大小完全相同，上面标有“红”“船”“精”“神”字样的四个彩球放入同一个不透明的袋子.问：

(1)、小慧在袋子中随机摸出一个彩球，不放回，再摸出一个彩球，请用树状图或者列表法列举出两次摸球可能出现的各种结果；

(2)、在（1）的条件下能拼出“红船”的概率是多少？

查看试题解析
23. 在 $6 \times 6$ 的方格纸中，点A，B，C，D，E都在格点上.

(1)、在图1中，AB交格子线于点P，求 $\frac{P B}{P A}$ 的值；

(2)、如图2，只用无刻度的直尺，作出 $△ C D E$ 的重心G.

查看试题解析
24. 如图，AD为 $△ A B C$ 的角平分线，点E，F在边AB上， $A E = A C$ ， FC交AD于点G.若 $∠ A D C = 60 °$ ， $F B = F C$ ， $D G = 2$ ， $C D = 3$ .

(1)、求 $∠ B D E$ 的度数.

(2)、求BD的长.

查看试题解析
25. 外出佩戴医用口罩能有效预防新型冠状病毒.某公司生产医用口罩供应市场，每件制造成本为1.8元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系满足下表.
销售单价x（元/件）
…
2
2.5
3
4
…
每月销售量y（万件）
…
6
5
4
2
…

(1)、在你学过的一次函数、反比例函数和二次函数等三种函数中，哪种函数能恰当地描述y与x的变化规律，并直接写出函数表达式；

(2)、当销售单价为多少元时，公司每月获得的利润为4.4万元？

(3)、如果公司每月的制造成本不超过5.4万元，那么当销售单价为多少元时，公司每月获得的利润最大？最大利润为多少万元？

查看试题解析
26. 如图，在直角坐标系中，抛物线 $y = a x^{2} + b x + 8 (a \neq 0)$ 经过点 $A (- 3 ， 5)$ ， $B (5 ， 3)$ ，交y轴于点C，以AB为直径的圆，经过点O，C，交x轴于点D，连结AO，AC.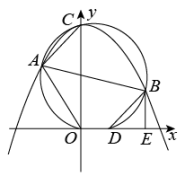

(1)、求抛物线的函数表达式；

(2)、求点D的坐标；

(3)、点E在x轴上，连结BD，BE.当 $△ B D E$ 与 $△ O A C$ 相似时，求满足条件的OE长.

查看试题解析

抽取件数（件）	100	150	200	500	800	1000
合格频数	900	141	189	474	760	950
合格频率	0.90	0.94	0.945	0.948	0.95	0.95

销售单价x（元/件）	…	2	2.5	3	4	…
每月销售量y（万件）	…	6	5	4	2	…