浙江省杭州市上城区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-22 类型:期末考试
一、单选题
-
1. 下列函数中,是二次函数的是( )A、y=2x-3 B、 C、y=(x-5)2-x2 D、y=x(1-x)2. 下列事件中是必然事件的是( )A、任意一个五边形的外角和等于540° B、投掷一枚均匀的硬币100次,正面朝上的次数为50次 C、367个同学参加一个聚会,他们中至少有两个同学的生日是同月同日 D、今年冬天会下雪3. 在平面直角坐标系中,将抛物线y=x2先向左平移3个单位,再向上平移2个单位,得到的抛物线表达式为( )A、y=(x+3)2+2 B、y=(x+3)2-2 C、x=(x-3)2+2 D、y=(x-3)2-24. 两个相似三角形的最短边分别是5cm和3cm,它们的周长之差为12cm,那么小三角形的周长为( )A、14cm B、16cm C、18cm D、30cm5. 如果规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,就称此图形为旋转对称图形,旋转的角度称为旋转角.下列图形是旋转对称图形,且有一个旋转角为60°的是( )A、正三角形 B、正方形 C、正六边形 D、正八边形6. 如图,小明在A时测得某树的影长为 , B时又测得该树的影长为 , 若两次日照的光线互相垂直,则树的高度为( )
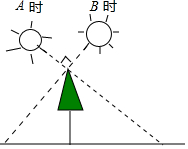 A、 B、 C、 D、7. 函数y=ax2+bx+c的图象如图所示,则选项中函数y=a(x﹣b)2+c的图象正确的是( )
A、 B、 C、 D、7. 函数y=ax2+bx+c的图象如图所示,则选项中函数y=a(x﹣b)2+c的图象正确的是( )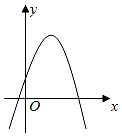 A、
A、 B、
B、 C、
C、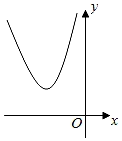 D、
D、 8. “苏堤南起南屏山麓,北到栖霞岭下,全长2.8公里.苏堤上有名的六吊桥由南到北分别是映波桥、锁澜桥、望山桥、压堤桥、东浦桥、跨虹桥.压堤桥约居苏堤南北的黄金分割位,旧时又是湖船东来西去的水道通行.”从地图上看,压堤桥位于苏堤北部,请结合上述描述,估计压堤桥到栖霞岭下的大致距离为( )A、0.9公里 B、1.1公里 C、1.3公里 D、1.4 公里9. 过山车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,点A,B,C为该抛物线上的三点,如图y表示运行的竖直高度(单位:m),x表示水平距离(单位:m).由此可推断出,此过山车运行到最低点时,所对应的水平距离x可能为( )
8. “苏堤南起南屏山麓,北到栖霞岭下,全长2.8公里.苏堤上有名的六吊桥由南到北分别是映波桥、锁澜桥、望山桥、压堤桥、东浦桥、跨虹桥.压堤桥约居苏堤南北的黄金分割位,旧时又是湖船东来西去的水道通行.”从地图上看,压堤桥位于苏堤北部,请结合上述描述,估计压堤桥到栖霞岭下的大致距离为( )A、0.9公里 B、1.1公里 C、1.3公里 D、1.4 公里9. 过山车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,点A,B,C为该抛物线上的三点,如图y表示运行的竖直高度(单位:m),x表示水平距离(单位:m).由此可推断出,此过山车运行到最低点时,所对应的水平距离x可能为( ) A、4 B、5 C、7 D、910. 如图,半圆O的直径AB=2,若点C,D在半圆上运动,且保持弦CD=1,延长AD、BC相交于点E.记∠E的度数为x°,△EDC的面积为y.则以下结论正确的是( )
A、4 B、5 C、7 D、910. 如图,半圆O的直径AB=2,若点C,D在半圆上运动,且保持弦CD=1,延长AD、BC相交于点E.记∠E的度数为x°,△EDC的面积为y.则以下结论正确的是( ) A、x随C,D运动而变化,y随C,D运动而变化 B、x不随C,D运动而变化,y不随C,D运动而变化 C、x随C,D运动而变化,y不随C,D运动而变化 D、x不随C,D运动而变化,y随C,D运动而变化
A、x随C,D运动而变化,y随C,D运动而变化 B、x不随C,D运动而变化,y不随C,D运动而变化 C、x随C,D运动而变化,y不随C,D运动而变化 D、x不随C,D运动而变化,y随C,D运动而变化二、填空题
-
11. 若扇形的圆心角为 ,半径为6,则扇形的面积为 .12. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码(绿码)示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 .
 13. 如图,AB是半圆O的直径,∠ABC=40°,则∠D=.
13. 如图,AB是半圆O的直径,∠ABC=40°,则∠D=. 14. 某个二次函数,当x≥1时,y随x的增大而增大,请写出一个满足条件的函数表达式.15. 为了测量河宽AB,某同学采用以下方法:如图,取一根标尺,把它横放,使CD∥AB,并使点B,D,O和点A,C,O分别在同一条直线上,量得CD=10米,OC=15米,OA=45米,则河宽AB=米.
14. 某个二次函数,当x≥1时,y随x的增大而增大,请写出一个满足条件的函数表达式.15. 为了测量河宽AB,某同学采用以下方法:如图,取一根标尺,把它横放,使CD∥AB,并使点B,D,O和点A,C,O分别在同一条直线上,量得CD=10米,OC=15米,OA=45米,则河宽AB=米. 16. 如图,已知点E为知形ABCD内一点,满足∠AEB=90°,延长DE交以CD为直径的半圆于点F,当AE=20,BE=15,DF=24时,则矩形AD边的长为.
16. 如图,已知点E为知形ABCD内一点,满足∠AEB=90°,延长DE交以CD为直径的半圆于点F,当AE=20,BE=15,DF=24时,则矩形AD边的长为.
三、解答题
-
17. 已知二次函数y=x2 , 当-1≤x≤2时,求函数y的最小值和最大值.小王的解答过程如下:
解:当x=-1时,y=1;
当x=2时,则y=4;
所以函数y的最小值为1,最大值为4
小王的解答过程正确吗?如果不正确,写出正确的解答过程.
18. 如图是三个可以自由转动的转盘,甲乙两人中,甲转动转盘,乙记录转盘停下时指针所指的数字.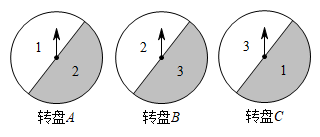 (1)、当转盘A和转盘B所指的数字之和为4时,就算甲赢,否则就算乙赢.请直接写出甲赢的概率.(2)、转动三个转盘得到三个数字,当这三个数字中有相同数时,就算甲赢,否则就算乙赢.请判断这个游戏是否公平,并说明理由.19. 如图,已知△ABC.
(1)、当转盘A和转盘B所指的数字之和为4时,就算甲赢,否则就算乙赢.请直接写出甲赢的概率.(2)、转动三个转盘得到三个数字,当这三个数字中有相同数时,就算甲赢,否则就算乙赢.请判断这个游戏是否公平,并说明理由.19. 如图,已知△ABC. (1)、作△ABC的外接圆,并在AB的上方作弦AD,使AD=BC.(要求尺规作图,保留作图痕迹,不写作法)(2)、连结CD,求证:CD∥AB.20. 加速度表示的是物体运动速度变化的大小,一个物体沿直线运动,且在运动的过程中加速度保持不变,则称这一物体在做匀加速直线运动.该物体初始速度为v0 , 加速度为a,加速时间t秒后速度为vt,由加速度定义可知:vt=v0+at,整个加速期的平均速度为.若v0=3米/秒,a=1米/秒2(1)、求5秒加速期的平均速度?(2)、设匀加速直线运动的路程为s,求s关于t的函数表达式(匀加速直线运动的路程=运动时间×平均速度).21. 将一副三角尺如图1放置,其中AD为Rt△ABC中BC边上的高,DE,DF分别交AB,AC于点M和N.
(1)、作△ABC的外接圆,并在AB的上方作弦AD,使AD=BC.(要求尺规作图,保留作图痕迹,不写作法)(2)、连结CD,求证:CD∥AB.20. 加速度表示的是物体运动速度变化的大小,一个物体沿直线运动,且在运动的过程中加速度保持不变,则称这一物体在做匀加速直线运动.该物体初始速度为v0 , 加速度为a,加速时间t秒后速度为vt,由加速度定义可知:vt=v0+at,整个加速期的平均速度为.若v0=3米/秒,a=1米/秒2(1)、求5秒加速期的平均速度?(2)、设匀加速直线运动的路程为s,求s关于t的函数表达式(匀加速直线运动的路程=运动时间×平均速度).21. 将一副三角尺如图1放置,其中AD为Rt△ABC中BC边上的高,DE,DF分别交AB,AC于点M和N. (1)、求证:△AMD∽△CND;(2)、如图2,将Rt△DEF绕点D旋转,此时EF∥BC,且E,A,F共线,判断是否成立,并给出证明.22. 二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的自变量x与函数值y的部分对应值如表:
(1)、求证:△AMD∽△CND;(2)、如图2,将Rt△DEF绕点D旋转,此时EF∥BC,且E,A,F共线,判断是否成立,并给出证明.22. 二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的自变量x与函数值y的部分对应值如表:x
……
-1
0
1
2
……
y
……
0
-2
-2
n
……
(1)、直接写出n的值,并求该二次函数的解析式;(2)、点Q(m,4)能否在该函数图象上?若能,请求出m的值,若不能,请说明理由.23. 已知Rt△ABC,两直角边AB与AC之和为4,作△ABC的外接圆,点O为圆心. (1)、如图1,连接OA,当90°时,求OA的值.(2)、如图2,过点A作AD⊥BC于点D,点E为AC中点,连接DE,求证:2∠ADE.(3)、如图3,作∠BAC的平分线交BC于点F,线段AF是否存在最大值?若存在,请求出AF的最大值;若不存在,请说明理由.
(1)、如图1,连接OA,当90°时,求OA的值.(2)、如图2,过点A作AD⊥BC于点D,点E为AC中点,连接DE,求证:2∠ADE.(3)、如图3,作∠BAC的平分线交BC于点F,线段AF是否存在最大值?若存在,请求出AF的最大值;若不存在,请说明理由.