浙江省杭州市拱墅区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-11-22 类型:期末考试
一、单选题
-
1. 下列事件中,属于必然事件的是( )A、在一个只装有白球和黑球的袋中摸出红球 B、一个三角形三个内角的和小于180° C、若是实数,则 D、在一张纸上任意画两条线段,这两条线段相交2. 如图,点在上,若 , 则( )
 A、40° B、50° C、70° D、80°3. 将函数的图象向上平移2个单位,所得图像对应的函数表达式是( )A、 B、 C、 D、4. 如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A、40° B、50° C、70° D、80°3. 将函数的图象向上平移2个单位,所得图像对应的函数表达式是( )A、 B、 C、 D、4. 如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )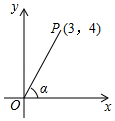 A、 B、 C、 D、5. 已知一个三角形的三边长分别为2,3,4,与其相似的另一个三角形的周长为36,则它的最长边的长为( )A、8 B、12 C、16 D、206. 如图,在中,点分别在边上,.若 , 则( )
A、 B、 C、 D、5. 已知一个三角形的三边长分别为2,3,4,与其相似的另一个三角形的周长为36,则它的最长边的长为( )A、8 B、12 C、16 D、206. 如图,在中,点分别在边上,.若 , 则( ) A、2 B、 C、3 D、7. 如图,在中, , 点为边的中点,以点为圆心,线段的长为半径画弧,与边交于点;以点为圆心,线段的长为半径画弧,与边交于点.若 , 则图中阴影部分的面积为( )
A、2 B、 C、3 D、7. 如图,在中, , 点为边的中点,以点为圆心,线段的长为半径画弧,与边交于点;以点为圆心,线段的长为半径画弧,与边交于点.若 , 则图中阴影部分的面积为( ) A、 B、 C、 D、8. 如图,四边形内接于 , 是的直径.若的半径为6, , 则的长度为( )
A、 B、 C、 D、8. 如图,四边形内接于 , 是的直径.若的半径为6, , 则的长度为( ) A、 B、 C、 D、9. 已知点(-1,y1),(1,m),(2,y2),(3,n),(4,y3)在二次函数y=x2+ax(a是常数)的图像上,若mn<0,则( )A、 B、 C、 D、10. 如图,在矩形中, , 点分别在边上,且与关于直线对称.点在边上,分别与交于两点.若 , , 则( )
A、 B、 C、 D、9. 已知点(-1,y1),(1,m),(2,y2),(3,n),(4,y3)在二次函数y=x2+ax(a是常数)的图像上,若mn<0,则( )A、 B、 C、 D、10. 如图,在矩形中, , 点分别在边上,且与关于直线对称.点在边上,分别与交于两点.若 , , 则( )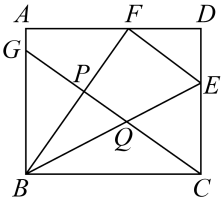 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算cos60°= .12. 若二次函数的图象过点 , 则的值是.13. 有一枚质地均匀的骰子,骰子各个面上的点数分别为1-6,任意抛掷这枚骰子,朝上面的点数大于2的概率是.14. 如图是用卡钳测量容量内径的示意图.若卡钳上两端点的距离为 , , 则容器的内径的长为.
 15. 如图,一个底部呈球形的烧瓶,球的半径为 , 瓶内原有液体的最大深度.部分液体蒸发后,瓶内液体的最大深度下降为 , 则截面圆中弦的长减少了(结果保留根号).
15. 如图,一个底部呈球形的烧瓶,球的半径为 , 瓶内原有液体的最大深度.部分液体蒸发后,瓶内液体的最大深度下降为 , 则截面圆中弦的长减少了(结果保留根号).
 16. 设二次函数y=ax2+bx+c(a,b,c是常数,a≠0),如表列出了x、y的部分对应值.
16. 设二次函数y=ax2+bx+c(a,b,c是常数,a≠0),如表列出了x、y的部分对应值.x
…
-5
-3
1
2
3
…
y
…
-2.79
m
-2.79
0
n
…
则不等式ax2+bx+c<0的解集是 , 方程ax2+bx+c=m的解是.
三、解答题
-
17. 一个布袋里装有三个小球,上面分别写着“1”,“2”,“3”,除数字外三个小球无其他差别.(1)、从布袋里任意摸出一个小球,求上面的数字恰好是“3”的概率.(2)、从布袋里任意摸出一个小球,记录其数字,放回并摇匀,再从中任意摸出一个小球,记录其数字,求两次记录的数字之和为3的概率.(要求列表或画树状图说明)18. 如图,测得两楼之间的水平距离为 , 从楼顶点观测点的俯角为45°,观测点的俯角为58°.分别求这两幢楼的高度(结果精确到).参考数据:.
 19. 一个斜抛物体的水平运动距离记为 , 对应的高度记为 , 与之间具有函数关系(常数,).已知当时,;当时,.(1)、求关于的函数表达式;(2)、求斜抛物体的最大高度和达到最大高度时的水平运动距离.20. 图,是的直径,弦于点 , 连接.
19. 一个斜抛物体的水平运动距离记为 , 对应的高度记为 , 与之间具有函数关系(常数,).已知当时,;当时,.(1)、求关于的函数表达式;(2)、求斜抛物体的最大高度和达到最大高度时的水平运动距离.20. 图,是的直径,弦于点 , 连接. (1)、求证:;(2)、作于点 , 若的半径为5, , 求的长.
(1)、求证:;(2)、作于点 , 若的半径为5, , 求的长.

