2022-2023学年冀教版数学八上期末复习专题6 线段垂直平分线与角平分线
试卷更新日期:2022-11-22 类型:复习试卷
一、单选题(每题3分,共36分)
-
1. 如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( )
 A、10.5 B、15 C、12 D、182. 已知点P在 ABC的边BC上,且满足PA=PC , 则下列确定点P位置的尺规作图,正确的是( )A、
A、10.5 B、15 C、12 D、182. 已知点P在 ABC的边BC上,且满足PA=PC , 则下列确定点P位置的尺规作图,正确的是( )A、 B、
B、 C、
C、 D、
D、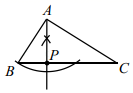 3. 已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( )
3. 已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( ) A、①② B、①③ C、②③ D、①②③4. 如图,在Rt△ABC中,观察作图痕迹,若BF=2,则CF的长为( )
A、①② B、①③ C、②③ D、①②③4. 如图,在Rt△ABC中,观察作图痕迹,若BF=2,则CF的长为( ) A、 B、3 C、2 D、5. 近年来,高速铁路的规划与建设成为各地政府争取的重要项目,如图,A,B,C三地都想将高铁站的修建项目落户在当地.但是,国资委为了使A,B,C三地的民众都能享受高铁带来的便利,决定将高铁站修建在到A,B,C三地距离都相等的地方,则高铁站应建在( )
A、 B、3 C、2 D、5. 近年来,高速铁路的规划与建设成为各地政府争取的重要项目,如图,A,B,C三地都想将高铁站的修建项目落户在当地.但是,国资委为了使A,B,C三地的民众都能享受高铁带来的便利,决定将高铁站修建在到A,B,C三地距离都相等的地方,则高铁站应建在( ) A、AB,BC两边垂直平分线的交点处 B、AB,BC两边高线的交点处 C、AB,BC两边中线的交点处 D、∠B,∠C两内角的平分线的交点处6. 如图,四边形中, , , 我们把这种两组邻边分别相等的四边形叫做“筝形”.下列关于筝形的结论正确的是( )
A、AB,BC两边垂直平分线的交点处 B、AB,BC两边高线的交点处 C、AB,BC两边中线的交点处 D、∠B,∠C两内角的平分线的交点处6. 如图,四边形中, , , 我们把这种两组邻边分别相等的四边形叫做“筝形”.下列关于筝形的结论正确的是( ) A、对角线AC,BD互相垂直平分 B、对角线BD平分∠ABC,∠ADC C、直线AC,BD是筝形的两条对称轴 D、筝形的面积等于对角线AC与BD的乘积7. 如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=4cm,则点D到AB的距离DE是( )
A、对角线AC,BD互相垂直平分 B、对角线BD平分∠ABC,∠ADC C、直线AC,BD是筝形的两条对称轴 D、筝形的面积等于对角线AC与BD的乘积7. 如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=4cm,则点D到AB的距离DE是( ) A、5cm B、4cm C、3cm D、2cm8. 如图,AD是的角平分线, , 若 , 则的面积为( )
A、5cm B、4cm C、3cm D、2cm8. 如图,AD是的角平分线, , 若 , 则的面积为( )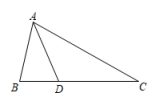 A、3 B、2 C、 D、19. 如图,点O在内,且到三边的距离相等,∠A=64°,则∠BOC的度数为( )
A、3 B、2 C、 D、19. 如图,点O在内,且到三边的距离相等,∠A=64°,则∠BOC的度数为( ) A、58° B、64° C、122° D、124°10. 如图,在△ABC中,若分别以AB、AC为边作△ABD和△ACE,且∠DAB=∠CAE=α,AD=AB,AC=AE,DC、BE交于点P,连接AP,则∠APC的度数为( )
A、58° B、64° C、122° D、124°10. 如图,在△ABC中,若分别以AB、AC为边作△ABD和△ACE,且∠DAB=∠CAE=α,AD=AB,AC=AE,DC、BE交于点P,连接AP,则∠APC的度数为( ) A、90°﹣α B、90°+α C、90°﹣α D、90°+α11. 如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+ ∠C;②当∠C=60°时,AF+BE=AB; ③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( )
A、90°﹣α B、90°+α C、90°﹣α D、90°+α11. 如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+ ∠C;②当∠C=60°时,AF+BE=AB; ③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( ) A、①② B、②③ C、①②③ D、①③12. 如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB+BC=BE,则∠B的度数是( )
A、①② B、②③ C、①②③ D、①③12. 如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB+BC=BE,则∠B的度数是( )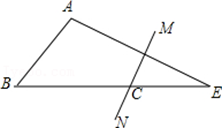 A、45° B、60° C、50° D、55°
A、45° B、60° C、50° D、55°二、填空题(每题3分,共18分)
-
13. 如图,在 中,直线 垂直平分 ,垂足为 ,交 于点 ,若 的周长为 , ,则 的长为.
 14. 如图,△ABC中,线段BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=84°,则∠BDC= °.
14. 如图,△ABC中,线段BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=84°,则∠BDC= °.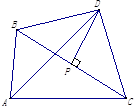 15. 如图,BD平分∠ABC,DE⊥AB于点E,DF⊥BC于点F,AB=7,BC=8.若 , 则DE= .
15. 如图,BD平分∠ABC,DE⊥AB于点E,DF⊥BC于点F,AB=7,BC=8.若 , 则DE= . 16. 如图,AD是Rt△ABC的角平分线,AB=12,AC=8,则△ABD的面积与△ACD的面积之比是 .
16. 如图,AD是Rt△ABC的角平分线,AB=12,AC=8,则△ABD的面积与△ACD的面积之比是 . 17. 如图,在△ABC中,DH是AC的垂直平分线,且与AC、BC分别交于点H、D;MN是AB的垂直平分线,且与AB、BC分别交于点M、N,连接AD、AN,已知∠BAC=74°,则∠DAN= .
17. 如图,在△ABC中,DH是AC的垂直平分线,且与AC、BC分别交于点H、D;MN是AB的垂直平分线,且与AB、BC分别交于点M、N,连接AD、AN,已知∠BAC=74°,则∠DAN= . 18. 在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC , ∠CDE=55°.如图,则∠EAB的度数为
18. 在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC , ∠CDE=55°.如图,则∠EAB的度数为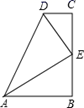
三、作图题
-
19. 如图,在中,
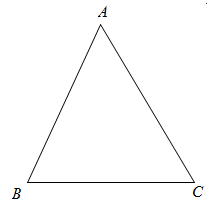
( 1 )尺规作图:作的平分线;
( 2 )尺规作图:作线段的垂直平分线;(不写作法,保留作图痕迹)
( 3 )若与交于点 , ∠ACP=24°,求的度数.
四、解答题
-
20. 如图所示,在中,∠C=90°,AD平分∠BAC,AB=2AC.求证:点D在线段AB的垂直平分线上.
 21. 如图,AD与BC相交于点O, , , ,试探索OE与BD的位置关系,并说明理由.
21. 如图,AD与BC相交于点O, , , ,试探索OE与BD的位置关系,并说明理由. 22. 如图,在中,是的中点, , , 垂足分别是 , .
22. 如图,在中,是的中点, , , 垂足分别是 , .
(Ⅰ)若 , 求证:是的角平分线;
(Ⅱ)若是的角平分线,求证: .
五、综合题
-
23. 已知 是 的平分线,点 是射线 上一点,点C、D分别在射线 、 上,连接PC、PD .
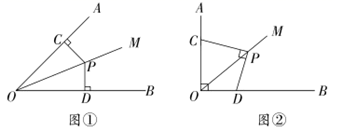 (1)、发现问题
(1)、发现问题如图①,当 , 时,则PC与PD的数量关系是 .
(2)、探究问题如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当 时,PC与PD在(1)中的数量关系还成立吗?说明理由.
-