广东省汕尾市2021-2022学年高二上学期数学期末考试试卷

试卷更新日期：2022-11-22 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} - 4 \leq 0}$ ， $B = {x | x > 1}$ ，则 $A ∩ B =$ （）

A、 $[- 2 ， 1)$ B、 $(- 2 ， 1)$ C、 $(1 ， 2]$ D、 $(1 ， 2)$

查看试题解析
2. 中心在原点的双曲线C的右焦点为 $(2 ， 0)$ ，实轴长为2，则双曲线C的方程为（）

A、 $\frac{x^{2}}{3} - y^{2} = 1$ B、 $x^{2} - \frac{y^{2}}{\sqrt{3}} = 1$ C、 $y^{2} - \frac{x^{2}}{3} = 1$ D、 $x^{2} - \frac{y^{2}}{3} = 1$

查看试题解析
3. 圆 $x^{2} + y^{2} = 4$ 与圆 $C ： {(x - 2)}^{2} + {(y - 1)}^{2} = 9$ 的位置关系是（）

A、内切 B、相交 C、外切 D、相离

查看试题解析
4. 设 $S_{n}$ 为等差数列 ${a_{n}}$ 的前 $n$ 项和， $S_{8} = 4 a_{3}$ ， $a_{7} = - 2$ ，则 $a_{9} =$ （）

A、-6 B、-4 C、-2 D、2

查看试题解析
5. 下列函数中，以 $π$ 为最小正周期，且在 $(\frac{π}{2} ， π)$ 上单调递减的为（）

A、 $y = t a n x$ B、 $y = | s i n x |$ C、 $y = | c o s x |$ D、 $y = c o s 2 x$

查看试题解析
6. 函数 $f (x) = \frac{1}{2^{x}} - l n x$ ，若实数 $x_{0}$ 是函数 $f (x)$ 的零点，且 $x_{1} > x_{0}$ ，则（）

A、 $f (x_{1}) < 0$ B、 $f (x_{1}) = 0$ C、 $f (x_{1}) > 0$ D、 $f (x_{1})$ 无法确定

查看试题解析
7. 在递增等比数列 ${a_{n}}$ 中， $S_{n}$ 为其前n项和．已知 $a_{1} + a_{n} = 34$ ， $a_{3} a_{n - 2} = 64 (n > 2 ， n \in N^{*})$ ，且 $S_{n} = 42$ ，则数列 ${a_{n}}$ 的公比为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 已知 $F$ 是双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左焦点， $A$ 为右顶点， $P$ 是双曲线 $C$ 上的点， $P F ⊥ x$ 轴，若 $| P F | = \frac{1}{4} | A F |$ ，则双曲线 $C$ 的离心率为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{5}{4}$ D、5

查看试题解析

二、多选题

9. 已知直线 $l ： x - m y + m - 1 = 0$ ，则下述正确的是（）

A、直线l的斜率可以等于 $0$ B、直线l的斜率有可能不存在 C、直线l可能过点 $(2 ， 1)$ D、若直线l的横纵截距相等，则 $m = \pm 1$

查看试题解析
10. 已知曲线C的方程为 $\frac{x^{2}}{k - 2} + \frac{y^{2}}{6 - k} = 1$ （ $k \in R$ ，且 $k \neq 2$ ， $k \neq 6$ ），则下列结论正确的是（）

A、当 $k = 4$ 时，曲线C为圆 B、若曲线C为椭圆，且焦距为 $2 \sqrt{2}$ ，则 $k = 5$ C、当 $k < 2$ 或 $k > 6$ 时，曲线C为双曲线 D、当曲线C为双曲线时，焦距等于4

查看试题解析
11. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{2}$ 与 $a_{6}$ 是方程 $x^{2} - 8 x + 12 = 0$ 的两根，则下列说法正确的是（）

A、若 ${a_{n}}$ 是等差数列，则 $a_{4} = - 4$ B、若 ${a_{n}}$ 是等比数列，则 $a_{4} = 2 \sqrt{3}$ C、若 ${a_{n}}$ 是递减等差数列，则当 $S_{n}$ 取得最大值时， $n = 7$ 或 $8$ D、若 ${a_{n}}$ 是递增等差数列， $2 S_{n} + 16 \geq n t$ 对 $n \in N^{*}$ 恒成立，则 $t \leq 8$

查看试题解析
12. 如图，棱长均为2的平行六面体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A A_{1} ⊥$ 平面ABCD， $∠ B A D = 60 °$ ， E，F分别是线段BD和线段 $A D_{1}$ 上的动点，且满足 $\overset{⇀}{A F} = λ \vec{A D_{1}}$ ， $\vec{B E} = (1 - λ) \vec{B D}$ ，则（）

A、当 $λ = \frac{1}{3}$ 时， $E F ⊥ B D$ B、当 $λ = \frac{1}{2}$ 时，直线EF与直线 $C C_{1}$ 所成角的大小为 $\frac{π}{4}$ C、当 $λ = \frac{1}{2}$ 时，若 $\vec{E F} = x \vec{A B} + y \vec{A D} + z \vec{A A_{1}} (x ， y ， z \in R)$ ，则 $x + y + z = 1$ D、当 $λ \in (0 ， 1)$ 时，三棱锥 $F - A B E$ 体积的最大值为 $\frac{\sqrt{3}}{6}$

查看试题解析

三、填空题

13. 复数 $z = 1 + i$ （其中i为虚数单位）的共轭复数 $\bar{z} =$ ．

查看试题解析
14. 在空间直角坐标系 $O - x y z$ 中，向量 $\bar{v} = (1 ， 3 ， - 2)$ 为平面ABC的一个法向量，其中 $A (1 ， - 1 ， t)$ ， $B (3 ， 1 ， 4)$ ，则向量 $\vec{A B}$ 的坐标为．

查看试题解析
15. 瑞士数学家欧拉（Euler）1765年在所著的《三角形的几何学》一书中提出：任意三角形的外心、重心、垂心在同一条直线上，后人称这条直线为欧拉线．已知 $△ A B C$ 的顶点 $A (- 4 ， 0)$ ， $B (0 ， 4)$ ， $C (2 ， 0)$ ，则 $△ A B C$ 欧拉线的方程为．

查看试题解析
16. 已知抛物线 $C ： y^{2} = 2 p x (p > 0)$ 的焦点为F，A为抛物线C上一点．以F为圆心，FA为半径的圆交抛物线C的准线于B，D两点，A，F，B三点共线，且 $| A F | = 4$ ，则 $p =$ ．

查看试题解析

四、解答题

17. 给出以下三个条件：① $S_{5} = 15$ ；② $a_{1}$ ， $a_{3}$ ， $a_{9}$ 成等比数列；③ $a_{6} = 3 a_{2}$ ．请从这三个条件中任选一个，补充到下面问题中，并完成作答．若选择多个条件分别作答，以第一个作答计分．
已知公差不为0的等差数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ， $S_{1} = 1$ ， ____．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = 3^{n}$ ，令 $c_{n} = a_{n} b_{n}$ ，求数列 ${c_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析
18. 某初中学校响应“双减政策”，积极探索减负增质举措，优化作业布置，减少家庭作业时间．现为调查学生的家庭作业时间，随机抽取了100名学生，记录他们每天完成家庭作业的时间（单位：分钟），将其分为 $[0 ， 10)$ ， $[10 ， 20)$ ， $[20 ， 30)$ ， $[30 ， 40)$ ， $[10 ， 50)$ ， $[50 ， 60]$ 六组，其频率分布直方图如下图：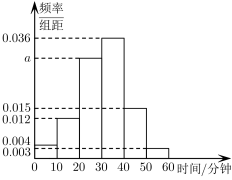

(1)、求 $a$ 的值，并估计这 $100$ 名学生完成家庭作业时间的中位数（中位数结果保留一位小数）；

(2)、现用分层抽样的方法从第三组 $[20 ， 30)$ 和第五组 $[40 ， 50)$ 中随机抽取6名学生进行“双减政策”情况访谈，再从访谈的学生中选取2名学生进行成绩跟踪，求被选作成绩跟踪的2名学生中，第三组和第五组各有1名的概率．

查看试题解析
19. 已知圆C过两点 $A (- 2 ， 0)$ ， $B (2 ， 4)$ ，且圆心C在直线 $2 x - y - 4 = 0$ 上．

(1)、求圆C的方程；

(2)、过点 $P (6 ， 4 \sqrt{3})$ 作圆C的切线，求切线方程．

查看试题解析
20. 如图，在棱长为 $2$ 的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ 为 $A D$ 中点．

(1)、求二面角 $D - B D_{1} - E$ 的大小；

(2)、探究线段 $B_{1} C$ 上是否存在点 $F$ ，使得 $D F ∥$ 平面 $B D_{1} E$ ？若存在，确定点 $F$ 的位置；若不存在，说明理由．

查看试题解析
21. 如图，五边形 $A B C D E$ 为东京奥运会公路自行车比赛赛道平面设计图，根据比赛需要，在赛道设计时需预留出 $A C$ ， $A D$ 两条服务通道（不考虑宽度）， $D C$ ， $C B$ ， $B A$ ， $A E$ ， $E D$ 为赛道．现已知 $∠ A B C = ∠ A E D = \frac{2 π}{3}$ ， $∠ C A D = ∠ B A C = \frac{π}{4}$ ， $B C = 2 \sqrt{3}$ 千米， $C D = \sqrt{34}$ 千米．

(1)、求服务通道 $A D$ 的长．

(2)、在上述条件下，如何设计才能使折线赛道 $A E D$ （即 $A E + E D$ ）的长度最大，并求最大值．

查看试题解析
22. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，离心率为 $\frac{\sqrt{3}}{2}$ ，过左焦点 $F_{1}$ 的直线l与椭圆C交于A，B两点， $△ A B F_{2}$ 的周长为8．

(1)、求椭圆C的标准方程；

(2)、如图， $B_{1}$ ， $B_{2}$ 是椭圆C的短轴端点，P是椭圆C上异于点 $B_{1}$ ， $B_{2}$ 的动点，点Q满足 $Q B_{1} ⊥ P B_{1}$ ， $Q B_{2} ⊥ P B_{2}$ ，求证 $△ P B_{1} B_{2}$ 与 $△ Q B_{1} B_{2}$ 的面积之比为定值．

查看试题解析