2023年春季湘教版数学九年级下册第一章 《二次函数》单元检测B
试卷更新日期:2022-11-21 类型:单元试卷
一、单选题(每题3分,共30分)
-
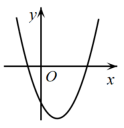
1. 关于二次函数 ,下列说法正确的是( )A、函数图象的开口向下 B、函数图象的顶点坐标是 C、该函数有最大值,是大值是5 D、当 时,y随x的增大而增大2. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )
 A、
A、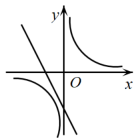 B、
B、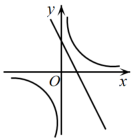 C、
C、 D、
D、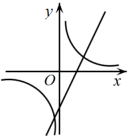 3. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其对称轴为直线x=﹣ , 且与x轴的一个交点坐标为(﹣2,0).下列结论:①abc>0;②a=b;③2a+c=0;④关于x的一元二次方程ax2+bx+c﹣1=0有两个相等的实数根.其中正确结论的序号是( )
3. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其对称轴为直线x=﹣ , 且与x轴的一个交点坐标为(﹣2,0).下列结论:①abc>0;②a=b;③2a+c=0;④关于x的一元二次方程ax2+bx+c﹣1=0有两个相等的实数根.其中正确结论的序号是( )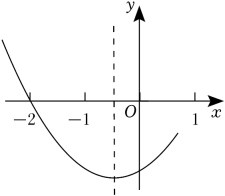 A、①③ B、②④ C、③④ D、②③4. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)abc<0;(2)4a+c>2b;(3)3b﹣2c>0;(4)若点A(﹣2,y1)、点B(﹣ , y2)、点C( , y3)在该函数图象上,则y1<y3<y2;(5)4a+2b≥m(am+b)(m为常数).其中正确的结论有( )
A、①③ B、②④ C、③④ D、②③4. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)abc<0;(2)4a+c>2b;(3)3b﹣2c>0;(4)若点A(﹣2,y1)、点B(﹣ , y2)、点C( , y3)在该函数图象上,则y1<y3<y2;(5)4a+2b≥m(am+b)(m为常数).其中正确的结论有( )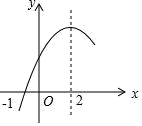 A、5个 B、4个 C、3个 D、2个5. 已知二次函数y=x2+ax+b(a,b为常数).命题①:该函数的图象经过点(1,0);命题②:该函数的图象经过点(3,0);命题③:该函数的图象与x轴的交点位于y轴的两侧;命题④;该函数的图象的对称轴为直线x=1.如果这四个命题中只有一个命题是假命题,则这个假命题是( )A、命题① B、命题② C、命题③ D、命题④6. 已知抛物线y=ax2+bx+c(a 0)经过点(1,0)和点(0,-3),且对称轴在y轴的左侧,则下列结论错误的是( )A、a>0 B、a+b=3 C、抛物线经过点(-1,0) D、关于x的一元二次方程ax2+bx+c=-1有两个不相等的实数根7. 如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( )
A、5个 B、4个 C、3个 D、2个5. 已知二次函数y=x2+ax+b(a,b为常数).命题①:该函数的图象经过点(1,0);命题②:该函数的图象经过点(3,0);命题③:该函数的图象与x轴的交点位于y轴的两侧;命题④;该函数的图象的对称轴为直线x=1.如果这四个命题中只有一个命题是假命题,则这个假命题是( )A、命题① B、命题② C、命题③ D、命题④6. 已知抛物线y=ax2+bx+c(a 0)经过点(1,0)和点(0,-3),且对称轴在y轴的左侧,则下列结论错误的是( )A、a>0 B、a+b=3 C、抛物线经过点(-1,0) D、关于x的一元二次方程ax2+bx+c=-1有两个不相等的实数根7. 如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( ) A、1 B、2 C、3 D、48. 如图,二次函数的图象与y轴的交点在(0,1)与(0,2)之间,对称轴为 , 函数最大值为4,结合图象给出下列结论:①;②;③;④若关于x的一元二次方程 有两个不相等的实数根,则m>4;⑤当x<0时,y随x的增大而减小.其中正确的结论有( )
A、1 B、2 C、3 D、48. 如图,二次函数的图象与y轴的交点在(0,1)与(0,2)之间,对称轴为 , 函数最大值为4,结合图象给出下列结论:①;②;③;④若关于x的一元二次方程 有两个不相等的实数根,则m>4;⑤当x<0时,y随x的增大而减小.其中正确的结论有( )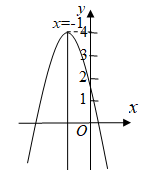 A、2个 B、3个 C、4个 D、5个9. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、410. 抛物线与y轴交于点C,过点C作直线l垂直于y轴,将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G,点 , 为图形G上两点,若 , 则m的取值范围是( )A、或 B、 C、 D、
A、2个 B、3个 C、4个 D、5个9. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、410. 抛物线与y轴交于点C,过点C作直线l垂直于y轴,将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G,点 , 为图形G上两点,若 , 则m的取值范围是( )A、或 B、 C、 D、二、填空题(每空3分,共18分)
-
11. 如图,一位篮球运动员投篮,球沿抛物线 运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为 3.05m ,则他距篮筐中心的水平距离 OH 是 m .
 12. 已知二次函数 , 当时,函数值y的最小值为1,则a的值为 .13. 在平面直角坐标系中,将抛物线先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是.14. 在平面直角坐标系 中,若抛物线 与x轴只有一个交点,则 .15. 如图,在平面直角坐标系中,点 在抛物线 上,过点A作y轴的垂线,交抛物线于另一点B , 点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 .
12. 已知二次函数 , 当时,函数值y的最小值为1,则a的值为 .13. 在平面直角坐标系中,将抛物线先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是.14. 在平面直角坐标系 中,若抛物线 与x轴只有一个交点,则 .15. 如图,在平面直角坐标系中,点 在抛物线 上,过点A作y轴的垂线,交抛物线于另一点B , 点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 . 16. 如图,二次函数 的图象与x轴的正半轴交于点A , 对称轴为直线 ,下面结论:
16. 如图,二次函数 的图象与x轴的正半轴交于点A , 对称轴为直线 ,下面结论: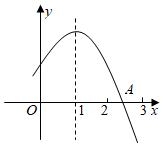
① ;
② ;
③ ;
④方程 必有一个根大于 且小于0.
其中正确的是(只填序号).
三、解答题(共8题,共72分)
-
17. 打油茶是广西少数民族特有的一种民俗,某特产公司近期销售一种盒装油茶,每盒的成本价为50元,经市场调研发现,该种油茶的月销售量y(盒)与销售单价x(元)之间的函数图象如图所示.
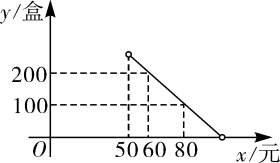 (1)、求y与x的函数解析式,并写出自变量x的取值范围;(2)、当销售单价定为多少元时,该种油茶的月销售利润最大?求出最大利润.18. 如图,抛物线 (b,c是常数)的顶点为C,与x轴交于A,B两点, , ,点P为线段 上的动点,过P作 交 于点Q.
(1)、求y与x的函数解析式,并写出自变量x的取值范围;(2)、当销售单价定为多少元时,该种油茶的月销售利润最大?求出最大利润.18. 如图,抛物线 (b,c是常数)的顶点为C,与x轴交于A,B两点, , ,点P为线段 上的动点,过P作 交 于点Q. (1)、求该抛物线的解析式;(2)、求 面积的最大值,并求此时P点坐标.19. 如图,抛物线经过点 , 点 , 与y轴交于点C,抛物线的顶点为D.
(1)、求该抛物线的解析式;(2)、求 面积的最大值,并求此时P点坐标.19. 如图,抛物线经过点 , 点 , 与y轴交于点C,抛物线的顶点为D. (1)、求抛物线的解析式;(2)、抛物线上是否存在点P,使的面积是面积的4倍,若存在,请直接写出点P的坐标:若不存在,请说明理由.20. 如图,二次函数的图象与y轴相交于点A,与反比例函数的图象相交于点B(3,1).
(1)、求抛物线的解析式;(2)、抛物线上是否存在点P,使的面积是面积的4倍,若存在,请直接写出点P的坐标:若不存在,请说明理由.20. 如图,二次函数的图象与y轴相交于点A,与反比例函数的图象相交于点B(3,1).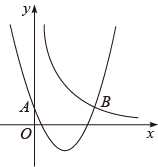 (1)、求这两个函数的表达式;(2)、当随x的增大而增大且时,直接写出x的取值范围;(3)、平行于x轴的直线l与函数的图象相交于点C、D(点C在点D的左边),与函数的图象相交于点E.若△ACE与△BDE的面积相等,求点E的坐标.21. 已知二次函数y=ax2+4ax+b.
(1)、求这两个函数的表达式;(2)、当随x的增大而增大且时,直接写出x的取值范围;(3)、平行于x轴的直线l与函数的图象相交于点C、D(点C在点D的左边),与函数的图象相交于点E.若△ACE与△BDE的面积相等,求点E的坐标.21. 已知二次函数y=ax2+4ax+b. (1)、求二次函数图象的顶点坐标(用含a,b的代数式表示);(2)、在平面直角坐标系中,若二次函数的图象与x轴交于A,B两点,AB=6,且图象过(1,c),(3,d),(−1,e),(−3,f)四点,判断c,d,e,f的大小,并说明理由;(3)、点M(m,n)是二次函数图象上的一个动点,当−2≤m≤1时,n的取值范围是−1≤n≤1,求二次函数的表达式.22. 如图,已知点M(x1 , y1),N(x2 , y2)在二次函数y=a(x﹣2)2﹣1(a>0)的图象上,且x2﹣x1=3.
(1)、求二次函数图象的顶点坐标(用含a,b的代数式表示);(2)、在平面直角坐标系中,若二次函数的图象与x轴交于A,B两点,AB=6,且图象过(1,c),(3,d),(−1,e),(−3,f)四点,判断c,d,e,f的大小,并说明理由;(3)、点M(m,n)是二次函数图象上的一个动点,当−2≤m≤1时,n的取值范围是−1≤n≤1,求二次函数的表达式.22. 如图,已知点M(x1 , y1),N(x2 , y2)在二次函数y=a(x﹣2)2﹣1(a>0)的图象上,且x2﹣x1=3. (1)、若二次函数的图象经过点(3,1).
(1)、若二次函数的图象经过点(3,1).①求这个二次函数的表达式;
②若y1=y2 , 求顶点到MN的距离;
(2)、当x1≤x≤x2时,二次函数的最大值与最小值的差为1,点M,N在对称轴的异侧,求a的取值范围.23. 如图1,抛物线y=ax2+x+c(a≠0)与x轴交于A(﹣2,0),B(6,0)两点,与y轴交于点C,点P是第一象限内抛物线上的一个动点,过点P作PD⊥x轴,垂足为D,PD交直线BC于点E,设点P的横坐标为m.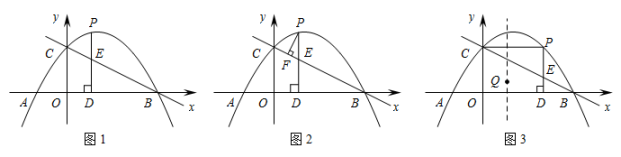 (1)、求抛物线的表达式;(2)、设线段PE的长度为h,请用含有m的代数式表示h;(3)、如图2,过点P作PF⊥CE,垂足为F,当CF=EF时,请求出m的值;(4)、如图3,连接CP,当四边形OCPD是矩形时,在抛物线的对称轴上存在点Q,使原点O关于直线CQ的对称点O′恰好落在该矩形对角线所在的直线上,请直接写出满足条件的点Q的坐标.24. 如图①,已知抛物线L:y=x2+bx+c的图象经过点A(0,3),B(1,0),过点A作ACx轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.
(1)、求抛物线的表达式;(2)、设线段PE的长度为h,请用含有m的代数式表示h;(3)、如图2,过点P作PF⊥CE,垂足为F,当CF=EF时,请求出m的值;(4)、如图3,连接CP,当四边形OCPD是矩形时,在抛物线的对称轴上存在点Q,使原点O关于直线CQ的对称点O′恰好落在该矩形对角线所在的直线上,请直接写出满足条件的点Q的坐标.24. 如图①,已知抛物线L:y=x2+bx+c的图象经过点A(0,3),B(1,0),过点A作ACx轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.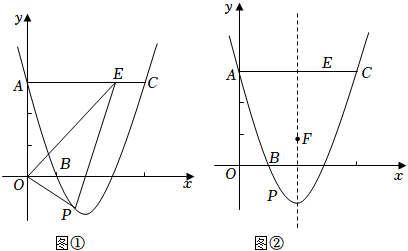 (1)、求抛物线的关系式;(2)、若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)、将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE内(包括△OAE的边界),求h的取值范围;(4)、如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)、求抛物线的关系式;(2)、若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)、将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE内(包括△OAE的边界),求h的取值范围;(4)、如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.