2023年春季湘教版数学九年级下册第一章《二次函数》单元检测A

试卷更新日期：2022-11-21 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 关于二次函数 $y = 2 {(x - 4)}^{2} + 6$ 的最大值或最小值，下列说法正确的是（）

A、有最大值4 B、有最小值4 C、有最大值6 D、有最小值6

查看试题解析
2. 将抛物线 $y = 2 {(x - 3)}^{2} + 2$ 向左平移3个单位长度，再向下平移2个单位长度，得到抛物线的解析式是（）

A、 $y = 2 {(x - 6)}^{2}$ B、 $y = 2 {(x - 6)}^{2} + 4$ C、 $y = 2 x^{2}$ D、 $y = 2 x^{2} + 4$

查看试题解析
3. 已知二次函数 $y = a {(x - 1)}^{2} - a (a \neq 0)$ ，当 $- 1 \leq x \leq 4$ 时，y的最小值为 $- 4$ ，则a的值为（）

A、 $\frac{1}{2}$ 或4 B、 $\frac{4}{3}$ 或 $- \frac{1}{2}$ C、 $- \frac{4}{3}$ 或4 D、 $- \frac{1}{2}$ 或4

查看试题解析
4. 已知二次函数 $y = a x^{2} + b x + c$ 的部分图象如图所示，对称轴为直线 $x = - 1$ ，有以下结论：① $a b c < 0$ ；②若t为任意实数，则有 $a - b t \leq a t^{2} + b$ ；③当图象经过点 $(1 ， 3)$ 时，方程 $a x^{2} + b x + c - 3 = 0$ 的两根为 $x_{1}$ ， $x_{2}$ （ $x_{1} < x_{2}$ ），则 $x_{1} + 3 x_{2} = 0$ ，其中，正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
5. 已知二次函数 $y = 2 x^{2} - 4 x + 5$ ，当函数值y随x值的增大而增大时，x的取值范围是（）

A、 $x < 1$ B、 $x > 1$ C、 $x < 2$ D、 $x > 2$

查看试题解析
6. 如图，二次函数y＝ax²+bx+c（a为常数，且a≠0）的图象过点(﹣1，0)，对称轴为直线x＝1，且2＜c＜3，则下列结论正确的是（）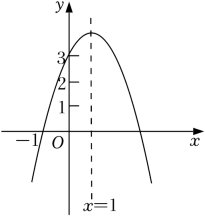

A、abc＞0 B、3a+c＞0 C、a²m²+abm≤a²+ab（m为任意实数） D、﹣1＜a＜﹣ $\frac{2}{3}$

查看试题解析
7. 如图，已知二次函数y＝ax²+bx+c（a、b、c为常数，且a≠0）的图象顶点为P（1，m），经过点A（2，1）；有以下结论：①a<0；②abc＞0；③4a+2b+c＝1；④x>1时，y随x的增大而减小；⑤对于任意实数t，总有at²+bt≤a+b，其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
8. 如图，已知开口向下的抛物线 $y = a x^{2} + b x + c$ 与x轴交于点 $(- 1 ， 0)$ 对称轴为直线 $x = 1$ .则下列结论：① $a b c > 0$ ；② $2 a + b = 0$ ；③函数 $y = a x^{2} + b x + c$ 的最大值为 $- 4 a$ ；④若关于x的方数 $a x^{2} + b x + c = a + 1$ 无实数根，则 $- \frac{1}{5} < a < 0$ .正确的有（）

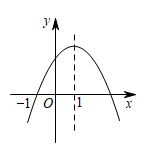A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知抛物线 $y = a x^{2} + b x + c$ 的图象与 $x$ 轴交于点 $A (- 2 ， 0)$ 、 $B (4 ， 0)$ ，若以 $A B$ 为直径的圆与在 $x$ 轴下方的抛物线有交点，则 $a$ 的取值范围是（）

A、 $a \geq \frac{1}{3}$ B、 $a > \frac{1}{3}$ C、 $0 < a < \frac{1}{3}$ D、 $0 < a \leq \frac{1}{3}$

查看试题解析
10. 如图，抛物线y＝ax²+bx+c与x轴交于两点（x₁ ， 0）、（2，0），其中0＜x₁＜1.下列四个结论：①abc＜0；②a+b+c＞0；③2a﹣c＞0；④不等式ax²+bx+c＞﹣ $\frac{c}{x_{1}}$ x+c的解集为0＜x＜x₁.其中正确结论的个数是（）

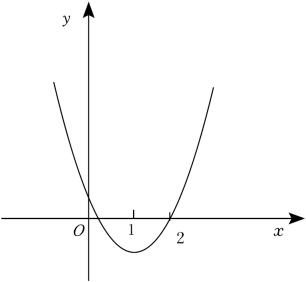A、4 B、3 C、2 D、1

查看试题解析

二、填空题（每空3分，共18分）

11. 汽车刹车后行驶的距离s与行驶时间t（秒）的函数关系是s＝15t﹣6t² ，汽车从刹车到停下来所用时间是秒.

查看试题解析
12. 如图是二次函数 $y = x^{2} + b x + c$ 的图像，该函数的最小值是．

查看试题解析
13. 若点 $P (m ， n)$ 在二次函数 $y = x^{2} + 2 x + 2$ 的图象上，且点 $P$ 到 $y$ 轴的距离小于2，则 $n$ 的取值范围是．

查看试题解析
14. 已知抛物线 $y = x^{2} + 2 x - n$ 与x轴交于A，B两点，抛物线 $y = x^{2} - 2 x - n$ 与x轴交于C，D两点，其中n＞0，若AD＝2BC，则n的值为.

查看试题解析
15. 若二次函数 $y = x^{2} - 2 x - 3$ 的图象上有且只有三个点到x轴的距离等于m，则m的值为．

查看试题解析
16. 已知抛物线 $y = x^{2} - 2 x - 3$ 与x轴交于A ， B两点（点A在点B的左侧），与y轴交于点C ，点 $D (4 ， y)$ 在抛物线上，E是该抛物线对称轴上一动点．当 $B E + D E$ 的值最小时， $△ A C E$ 的面积为．

查看试题解析

三、解答题（共8题，共72分）

17. 掷实心球是兰州市高中阶段学校招生体育考试的选考项目．如图1是一名女生投掷实心球，实心球行进路线是一条抛物线，行进高度y（m）与水平距离x（m）之间的函数关系如图2所示，抛出时起点处高度为 $\frac{5}{3} m$ ，当水平距离为3m时，实心球行进至最高点3m处．

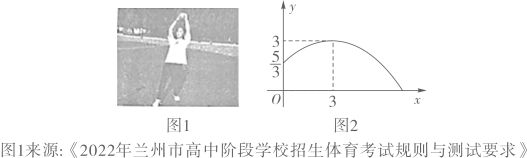(1)、求y关于x的函数表达式；

(2)、根据兰州市高中阶段学校招生体有考试评分标准（女生），投掷过程中，实心球从起点到落地点的水平距离大于等于6.70m，此项考试得分为满分10分．该女生在此项考试中是否得满分，请说明理由．

查看试题解析
18. 某商店购进了一种消毒用品，进价为每件8元，在销售过程中发现，每天的销售量y（件）与每件售价x（元）之间存在一次函数关系（其中8≤x≤15，且x为整数）．当每件消毒用品售价为9元时，每天的销售量为105件；当每件消毒用品售价为11元时，每天的销售量为95件．

(1)、求y与x之间的函数关系式．

(2)、若该商店销售这种消毒用品每天获得425元的利润，则每件消毒用品的售价为多少元？

(3)、设该商店销售这种消毒用品每天获利w（元），当每件消毒用品的售价为多少元时，每天的销售利润最大？最大利润是多少元？

查看试题解析
19. 为落实“双减”，老师布置了一项这样的课后作业：

二次函数的图象经过点 $(- 1 ， - 1)$ ，且不经过第一象限，写出满足这些条件的一个函数表达式．

(1)、 [观察发现]
请完成作业，并在直角坐标系中画出大致图象．

(2)、[思考交流]
小亮说：“满足条件的函数图象的对称轴一定在y轴的左侧．”
小莹说：“满足条件的函数图象一定在x轴的下方．”
你认同他们的说法吗？若不认同，请举例说明．

(3)、[概括表达]
小博士认为这个作业的答案太多，老师不方便批阅，于是探究了二次函数 $y = a x^{2} + b x + c$ 的图象与系数a，b，c的关系，得出了提高老师作业批阅效率的方法．

请你探究这个方法，写出探究过程．

查看试题解析
20. 如图，平行四边形 $A B C D$ 中， $A B = 5 ， B C = 10 ， B C$ 边上的高 $A M = 4$ ，点E为 $B C$ 边上的动点（不与B、C重合，过点E作直线 $A B$ 的垂线，垂足为F，连接 $D E 、 D F$ ．

(1)、求证： $△ A B M ∽ △ E B F$ ；

(2)、当点E为 $B C$ 的中点时，求 $D E$ 的长；

(3)、设 $B E = x ， △ D E F$ 的面积为y，求y与x之间的函数关系式，并求当x为何值时，y有最大值，最大值是多少？

查看试题解析
21. 如图1，抛物线 $y = x^{2} + b x + c$ 与x轴交于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与y轴交于点C.
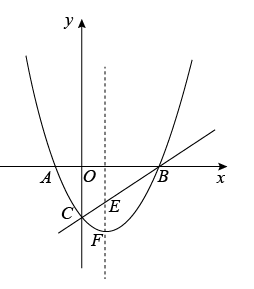
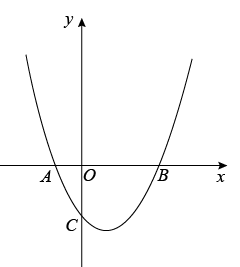
图1 图2

(1)、求该抛物线的解析式；

(2)、若点E是抛物线的对称轴与直线BC的交点，点F是抛物线的顶点，求EF的长；

(3)、设点P是（1）中抛物线上的一个动点，是否存在满足 $S_{△ P A B} = 6$ 的点P？如果存在，请求出点P的坐标；若不存在，请说明理由.（请在图2中探讨）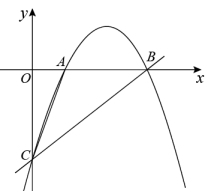

查看试题解析
22. 如图，抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴交于 $A$ ， $B$ 两点，与 $y$ 轴交于 $C$ 点，直线 $B C$ 方程为 $y = x - 3$ ．

(1)、求抛物线的解析式；

(2)、点 $P$ 为抛物线上一点，若 $S_{△ P B C} = \frac{1}{2} S_{△ A B C}$ ，请直接写出点 $P$ 的坐标；

(3)、点 $Q$ 是抛物线上一点，若 $∠ A C Q = 45 °$ ，求点 $Q$ 的坐标．

查看试题解析
23. 在平面直角坐标系中，抛物线y＝﹣ $\frac{1}{2}$ $x^{2}$ ＋（m﹣1）x＋2m与x轴交于A，B（4，0）两点，与y轴交于点C，点P是抛物线在第一象限内的一个动点．

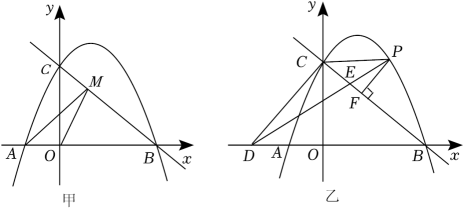(1)、求抛物线的解析式，并直接写出点A，C的坐标；

(2)、如图甲，点M是直线BC上的一个动点，连接AM，OM，是否存在点M使AM＋OM最小，若存在，请求出点M的坐标，若不存在，请说明理由；

(3)、如图乙，过点P作PF⊥BC，垂足为F，过点C作CD⊥BC，交x轴于点D，连接DP交BC于点E，连接CP．设△PEF的面积为S₁ ， △PEC的面积为S₂ ，是否存在点P，使得 $\frac{S_{1}}{S_{2}}$ 最大，若存在，请求出点P的坐标，若不存在，请说明理由．

查看试题解析
24. 已知抛物线 $C_{1} ： y = - \frac{1}{2} (m^{2} + 1) x^{2} - (m + 1) x - 1$ 与x轴有公共点．

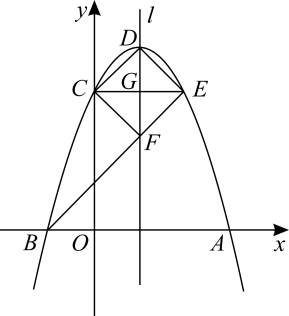(1)、当y随x的增大而增大时，求自变量x的取值范围；

(2)、将抛物线 $C_{1}$ 先向上平移4个单位长度，再向右平移n个单位长度得到抛物线 $C_{2}$ （如图所示），抛物线 $C_{2}$ 与x轴交于点A，B（点A在点B的右侧），与y轴交于点C．当OC＝OA时，求n的值；

(3)、D为抛物线 $C_{2}$ 的顶点，过点C作抛物线 $C_{2}$ 的对称轴l的垂线，垂足为G，交抛物线 $C_{2}$ 于点E，连接BE交l于点F．求证：四边形CDEF是正方形．

查看试题解析

2023年春季湘教版数学九年级下册第一章 《二次函数》单元检测A

一、单选题（每题3分，共30分）

二、填空题（每空3分，共18分）

三、解答题（共8题，共72分）

2023年春季湘教版数学九年级下册第一章《二次函数》单元检测A