山西省吕梁孝义市2022-2023学年九年级上学期期中质量监测数学试题
试卷更新日期:2022-11-21 类型:期中考试
一、单选题
-
1. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、2. “保护生态,人人有责”,下列生态环保图片中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列关于x的一元二次方程中,有两个不相等的实数根的是( )A、 B、 C、 D、4. 将抛物线向先左平移1个单位,再向上平移2个单位后,得到抛物线的解析式是( )A、 B、 C、 D、5. 若抛物线与x轴的两个交点为 , , 则该抛物线的对称轴为( )A、直线 B、直线 C、直线 D、直线6. 用直接开平方法解方程时,可以将其转化为或 , 其依据的数学知识是( )A、完全平方公式 B、平方根的意义 C、等式的性质 D、一元二次方程的求根公式7. 如图,在中, , , 将以C为旋转中心,顺时针旋转角度(),若的中点O恰好在AC上,则旋转角的度数是( )
3. 下列关于x的一元二次方程中,有两个不相等的实数根的是( )A、 B、 C、 D、4. 将抛物线向先左平移1个单位,再向上平移2个单位后,得到抛物线的解析式是( )A、 B、 C、 D、5. 若抛物线与x轴的两个交点为 , , 则该抛物线的对称轴为( )A、直线 B、直线 C、直线 D、直线6. 用直接开平方法解方程时,可以将其转化为或 , 其依据的数学知识是( )A、完全平方公式 B、平方根的意义 C、等式的性质 D、一元二次方程的求根公式7. 如图,在中, , , 将以C为旋转中心,顺时针旋转角度(),若的中点O恰好在AC上,则旋转角的度数是( ) A、 B、 C、 D、8. 抛物线的图象如图所示,则下列结论正确的是( )
A、 B、 C、 D、8. 抛物线的图象如图所示,则下列结论正确的是( ) A、 B、 C、 D、关于x的一元二次方程有两个不相等的实数根9. 某种植物的主干长出若干数目的支干,每个支干又长出相同数目的小分支,主干、支干、小分支的总数是111.若设每个支干长出的小分支的个数是x,则下面所列方程正确的是( )A、 B、 C、 D、10. 如图,线段 , 在线段AB上找一点C,C把分为和两段,其中 , 若 , 则点C就叫做线段的黄金分割点,其中(或)的值叫做黄金分割数.则黄金分割数是( )
A、 B、 C、 D、关于x的一元二次方程有两个不相等的实数根9. 某种植物的主干长出若干数目的支干,每个支干又长出相同数目的小分支,主干、支干、小分支的总数是111.若设每个支干长出的小分支的个数是x,则下面所列方程正确的是( )A、 B、 C、 D、10. 如图,线段 , 在线段AB上找一点C,C把分为和两段,其中 , 若 , 则点C就叫做线段的黄金分割点,其中(或)的值叫做黄金分割数.则黄金分割数是( )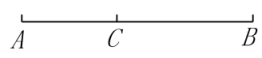 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在中, , , , 将以B为中心逆时针方向旋转,得到 , 当点C的对应点E落在边AB上时,线段AD的长度值是 .
 12. 若抛物线的顶点在x轴上,则c的值是 .13. 在2022年第56届国际乒联世界乒乓球团体锦标赛女团决赛中,国乒女团零封日本女团,实现五连冠,第22次捧起象征“最强女子乒团”的荣誉——考比伦杯.此次世锦赛小组赛中,中国乒乓球女队被分在A组,在本组单循环赛中(每两个队之间比赛一场)共进行了10场比赛,则在A组中共有个国家的女队参加了比赛.
12. 若抛物线的顶点在x轴上,则c的值是 .13. 在2022年第56届国际乒联世界乒乓球团体锦标赛女团决赛中,国乒女团零封日本女团,实现五连冠,第22次捧起象征“最强女子乒团”的荣誉——考比伦杯.此次世锦赛小组赛中,中国乒乓球女队被分在A组,在本组单循环赛中(每两个队之间比赛一场)共进行了10场比赛,则在A组中共有个国家的女队参加了比赛. 14. 已知点和都在二次函数的图象上,则和的大小关系是 .15. 有一块三角形材料如图所示, , , . 用这块材料剪出一个 , 其中,点D,E,F分别在 , , 上.则剪出的的面积的最大值是 .
14. 已知点和都在二次函数的图象上,则和的大小关系是 .15. 有一块三角形材料如图所示, , , . 用这块材料剪出一个 , 其中,点D,E,F分别在 , , 上.则剪出的的面积的最大值是 .
三、解答题
-
16. 解方程(1)、(2)、17. 已知抛物线 . 请用配方法将其化为的形式,并写出其开口方向、对称轴及顶点坐标.18. 某农户种植有图1所示蔬菜大棚,其截面示意图如图2所示,其横截面塑料顶棚可以近似看作是抛物线,其中是地面所在的水平线,点O是塑料顶棚与地面的交点,是保温墙,并且塑料顶棚最高点到点O的水平距离是6米,到地面的高度是3米.现以所在直线为x轴,过点O垂直于的直线为y轴,建立平面直角坐标系.若保温墙到点O的距离米.请你求出保温墙AB的高度.
 19. 如图,在平面直角坐标系中,(2,1),(4,3),(1,3).
19. 如图,在平面直角坐标系中,(2,1),(4,3),(1,3). (1)、若与关于原点成中心对称(点 , , 分别与点A,B,C对应),试在图中画出;(2)、将以C为中心顺时针旋转90°得到 , 试在图中画出;(3)、若可由以点P为中心旋转得到,则点P的坐标是 .20. 阅读下列材料,并完成相应学习任务:
(1)、若与关于原点成中心对称(点 , , 分别与点A,B,C对应),试在图中画出;(2)、将以C为中心顺时针旋转90°得到 , 试在图中画出;(3)、若可由以点P为中心旋转得到,则点P的坐标是 .20. 阅读下列材料,并完成相应学习任务:古希腊著名的毕达哥拉斯学派发现,一定数目的点或圆在等距离排列下可以形成一个等边三角形,他们把这样的数称之为三角形数.如用1,3,6,10,15,21,…数目的石子就可以排成如图1所示的等边三角形,因而这样的数就是三角形数.
所有的三角形数都具有如图2所示的规律.


学习任务:请用一元二次方程的有关知识,解决下列问题:
(1)、请判断78是第几个三角形数?写出判断过程.(2)、若相邻两个三角形数的和是121,求这两个三角形数.21. 山西土豆(马铃薯)色泽光鲜,含淀粉高,不容易腐烂,具有比其它地方土豆多淀粉、蛋白质、维生素C等营养成分.某合作社2020年到2022年每年种植土豆100亩,2020年土豆的平均亩产量为1000千克,2021年到2022年引进先进的种植技术,2022年土豆的平均亩产量达到1440千克.(1)、若2021年和2022年土豆的平均亩产量的年增长率相同,求土豆平均亩产量的年增长率为多少?(2)、2023年该合作社计划在保证土豆种植的总成本不变的情况下,增加土豆的种植面积,经过统计调查发现,2022年每亩土豆的种植成本为1200元,若土豆的种植面积每增加1亩,则每亩土豆的种植成本将下降10元,求该合作社增加土豆种植面积多少亩,才能保证土豆种植的总成本不变?22. 综合与实践问题情境:如图1,四边形和都是正方形,点G,F分别在边和上,点E在正方形的内部.
 (1)、猜想证明:
(1)、猜想证明:和的位置关系是 , 和的数量关系是 .
(2)、将正方形以C为中心顺时针方向旋转到图2所示位置,则(1)中的结论是否仍然成立?请说明理由.(3)、如图3,在正方形以C为中心顺时针旋转的过程中,当点E落在正方形的边上时,若 , , 则的长度是 . (请直接写出答案即可)23. 综合与探究如图1,抛物线与x轴交于A,B两点(点A在点B的左边),与y轴交于点C.点D在第一象限内的抛物线上.
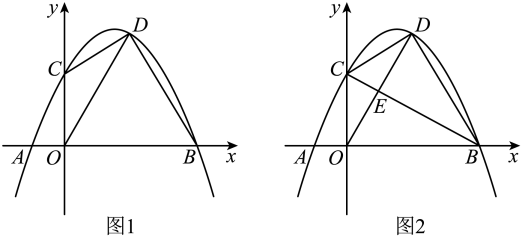 (1)、请直接写出点A,B,C的坐标;(2)、若 , 求出点D的坐标;(3)、如图2,在满足(2)的条件下,连接交于点E.则是否平分线段?请说明理由.
(1)、请直接写出点A,B,C的坐标;(2)、若 , 求出点D的坐标;(3)、如图2,在满足(2)的条件下,连接交于点E.则是否平分线段?请说明理由.