山东省烟台市龙口市(五四制)2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-11-21 类型:期中考试
一、单选题
-
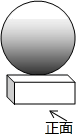
1. 在Rt△ABC中,∠C=90°,cosA= , AB=10,则AC的长为( )A、3 B、4 C、6 D、82. 如图,一个水晶球摆件,它是由一个长方体和一个球体组成的几何体,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 对于二次函数的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线 C、图象与x轴有两个交点 D、当时,y的值随x值的增大而减小5. 将抛物线向左平移1个单位长度,再向上平移2个单位长度,所得到的抛物线为( )A、 B、 C、 D、6. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )
3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 对于二次函数的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线 C、图象与x轴有两个交点 D、当时,y的值随x值的增大而减小5. 将抛物线向左平移1个单位长度,再向上平移2个单位长度,所得到的抛物线为( )A、 B、 C、 D、6. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )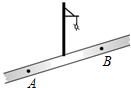 A、
A、 B、
B、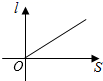 C、
C、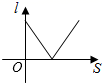 D、
D、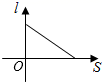 7. 已知点A(-3,y1),B(2,y2),C(3,y3)在抛物线y=2x2-4x+c上,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y2>y1 D、y2>y3>y18. 在正方形网格中,的位置如图所示,则的值为( )
7. 已知点A(-3,y1),B(2,y2),C(3,y3)在抛物线y=2x2-4x+c上,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y2>y1 D、y2>y3>y18. 在正方形网格中,的位置如图所示,则的值为( ) A、 B、 C、 D、9. 已知抛物线 ,a是常数,且 ,下列选项中可能是它大致图像的是( )A、
A、 B、 C、 D、9. 已知抛物线 ,a是常数,且 ,下列选项中可能是它大致图像的是( )A、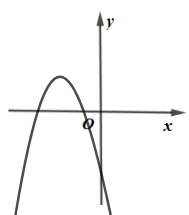 B、
B、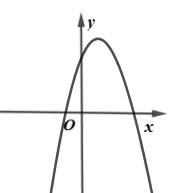 C、
C、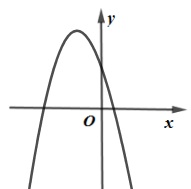 D、
D、 10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④a+b>m(am+b)(m≠1的实数),其中正确结论的个数为( )
10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④a+b>m(am+b)(m≠1的实数),其中正确结论的个数为( )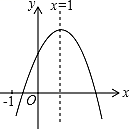 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
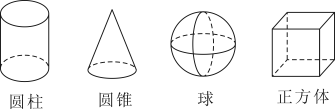
11. 若是关于x的二次函数,则m的值是 .12. △ABC中,∠A、∠B都是锐角,若sinA= ,cosB= ,则∠C=.13. 如图所示的4个几何体中,正投影可能是四边形的几何体共有个.
 14. 一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式 , 则小球距离地面的最大高度是米.15. 如图抛物线y=ax2与反比例函数交于点C(1,2),不等式的解集是 .
14. 一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式 , 则小球距离地面的最大高度是米.15. 如图抛物线y=ax2与反比例函数交于点C(1,2),不等式的解集是 .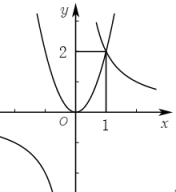 16. 如图是一种机器零件的示意图,其中米,米,则四边形的面积为米2
16. 如图是一种机器零件的示意图,其中米,米,则四边形的面积为米2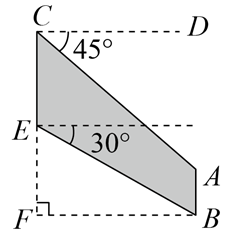
三、解答题
-
17. 计算: .18. 在中, , , .
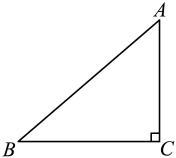 (1)、求的长;(2)、求的值.19. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示.
(1)、求的长;(2)、求的值.19. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示.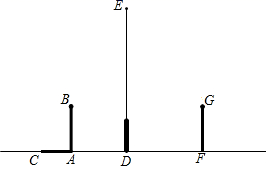 (1)、请你通过画图确定灯泡所在的位置.(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.20. 小尧用“描点法”画二次函数的 图像,列表如下:
(1)、请你通过画图确定灯泡所在的位置.(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.20. 小尧用“描点法”画二次函数的 图像,列表如下:x
…
-4
-3
-2
-1
0
1
2
…
y
…
5
0
-3
-4
-3
0
-5
…
 (1)、由于粗心,小尧算错了其中的一个 y值,请你指出这个算错的y值所对应的x=;(2)、在图中画出这个二次函数的图像;(3)、当 y≥5 时,x 的取值范围是 .21. 某公司研制出一种新颖的家用小电器,每件的生产成本为18元,经市场调研表明,按定价40元出售,每日可销售20件.为了增加销量,每降价1元,日销售量可增加2件.在确保盈利的前提下,当降价多少元时,每天的利润最大?最大利润是多少?22. 在直角坐标平面内,二次函数图象的顶点为 , 且过点 .
(1)、由于粗心,小尧算错了其中的一个 y值,请你指出这个算错的y值所对应的x=;(2)、在图中画出这个二次函数的图像;(3)、当 y≥5 时,x 的取值范围是 .21. 某公司研制出一种新颖的家用小电器,每件的生产成本为18元,经市场调研表明,按定价40元出售,每日可销售20件.为了增加销量,每降价1元,日销售量可增加2件.在确保盈利的前提下,当降价多少元时,每天的利润最大?最大利润是多少?22. 在直角坐标平面内,二次函数图象的顶点为 , 且过点 .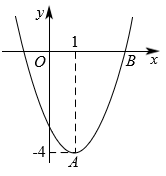 (1)、求该二次函数的表达式;(2)、将该二次函数图象沿x轴平移,使平移后所得图象经过坐标原点,请直接写出平移后所得图象与x轴的另一个交点的坐标.23. 为响应“创建全国文明城市”的号召,不断美化环境,我市拟修建一矩形绿地,绿地一边靠墙,可利用的墙长不超过18米,另外三边由40米长的栅栏围成,设矩形ABCD中,垂直于墙的边为米,面积为平方米(如图).
(1)、求该二次函数的表达式;(2)、将该二次函数图象沿x轴平移,使平移后所得图象经过坐标原点,请直接写出平移后所得图象与x轴的另一个交点的坐标.23. 为响应“创建全国文明城市”的号召,不断美化环境,我市拟修建一矩形绿地,绿地一边靠墙,可利用的墙长不超过18米,另外三边由40米长的栅栏围成,设矩形ABCD中,垂直于墙的边为米,面积为平方米(如图).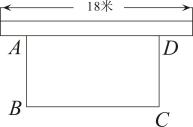 (1)、求与之间的函数关系式,并求出自变量的取值范围;(2)、求矩形的最大面积.24. 资阳市为实现5G网络全覆盖,2020-2025年拟建设5G基站七千个.如图,在坡度为的斜坡上有一建成的基站塔 , 小芮在坡脚C测得塔顶A的仰角为 , 然后她沿坡面行走13米到达D处,在D处测得塔顶A的仰角为(点A、B、C、D均在同一平面内)(参考数据:)
(1)、求与之间的函数关系式,并求出自变量的取值范围;(2)、求矩形的最大面积.24. 资阳市为实现5G网络全覆盖,2020-2025年拟建设5G基站七千个.如图,在坡度为的斜坡上有一建成的基站塔 , 小芮在坡脚C测得塔顶A的仰角为 , 然后她沿坡面行走13米到达D处,在D处测得塔顶A的仰角为(点A、B、C、D均在同一平面内)(参考数据:)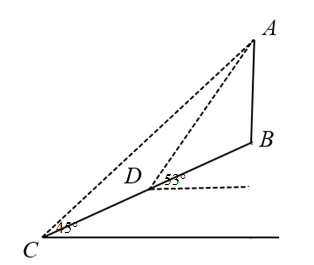 (1)、求D处的竖直高度;(2)、求基站塔的高.25. 已知抛物线y=ax2+5x+c交x轴于A,B两点,交y轴于点C,点A,C的坐标分别为(1,0),(0,-4).
(1)、求D处的竖直高度;(2)、求基站塔的高.25. 已知抛物线y=ax2+5x+c交x轴于A,B两点,交y轴于点C,点A,C的坐标分别为(1,0),(0,-4).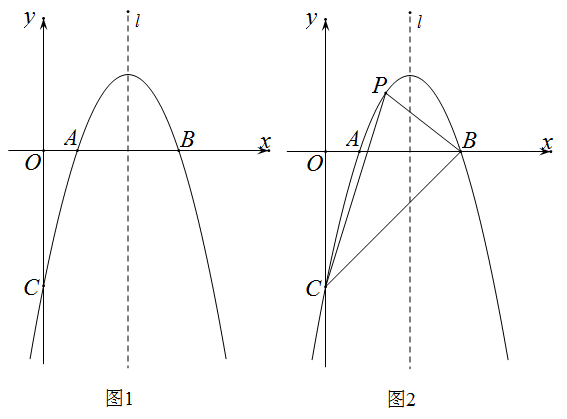 (1)、求抛物线的解析式;(2)、①如图1,直线l为抛物线的对称轴,请在直线l上找一点M,使得AM+CM最小,求出点M的坐标.
(1)、求抛物线的解析式;(2)、①如图1,直线l为抛物线的对称轴,请在直线l上找一点M,使得AM+CM最小,求出点M的坐标.②连接AC,求△ACM的面积.
(3)、如图2,P是在x轴上方抛物线上的一动点,连接BC,BP,当∠PBA=∠PBC时,求出直线BP的解析式.