江西省抚州市南城县2022-2023学年九年级上学期期中考数学试卷

试卷更新日期：2022-11-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列哪个方程是一元二次方程（）

A、 $x + 2 y = 1$ B、 $x^{2} - 2 x + 3 = 0$ C、 $x^{2} - \frac{1}{x} = 3$ D、 $x = 2 x^{3} - 3$

查看试题解析
2. 两个矩形的位置如图所示，若 $∠ 1 = 120 ° ，$ 则 $∠ 2$ 的度数为（）

A、 $30 °$ B、 $15 °$ C、 $60 °$ D、 $45 °$

查看试题解析
3. 如图， $l_{1} ∥ l_{2} ∥ l_{3}$ ，直线a、b与l₁、l₂、l₃分别相交于点A、B、C和点D、E、F，若 $\frac{A B}{B C}$ ＝ $\frac{2}{3}$ ， DE＝4，则EF的长是（）

A、 $\frac{20}{3}$ B、 $\frac{3}{2}$ C、1 D、6

查看试题解析
4. 若m是一元二次方程 $x^{2} - 5 x - 2 = 0$ 的一个实数根，则 $2022 - m^{2} + 5 m$ 的值是（）

A、2019 B、2020 C、2021 D、2022

查看试题解析
5. 某医院计划选派护士支援某地的防疫工作，甲、乙、丙、丁4 名护士积极报名参加，其中甲是共青团员，其余3 人均是共产党员．医院决定用随机抽取的方式确定人选．若需从这4 名护士中随机抽取2 人，那么被抽到的两名护士都是共产党员的概率（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、1

查看试题解析
6. 如图，点E、F分别在正方形ABCD的边CD、AD上，且EF垂直于BE，若AB＝8，BE＝10，则ABEF的周长为（）

A、25 B、26 C、27 D、28

查看试题解析

二、填空题

7. 若 $4 x = 5 y$ ，则 $\frac{x}{y}$ ＝．

查看试题解析
8. 如图，一个圆环被4条线段分成4个相等的区域，现有2022年冬奥会吉祥物“冰墩墩”和“雪容融”各一个，将这两个吉祥物放在任意两个区域内．吉祥物“冰墩墩”放在区域①的概率．

查看试题解析
9. 如图， $△ A B C$ 和 $△ D E F$ 是以点 $O$ 为位似中心的位似图形．若 $O A ： A D = 2 ： 3$ ，则 $△ A B C$ 与 $△ D E F$ 的周长比是．

查看试题解析
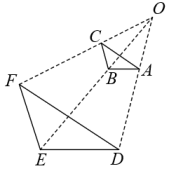10. 若关于x的一元二次方程x²+2x-k+3＝0有两个不相等的实数根，则k的取值范围是．

查看试题解析
11. 如图，将边长为3的正方形ABCD沿其对角线AC平移，使A的对应点A′满足AA′＝ $\frac{1}{3}$ AC，则所得正方形与原正方形重叠部分的面积是．

查看试题解析
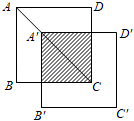12. 矩形ABCD中， $A B = 8$ ， $A D = 7$ ，点E在AB边上， $A E = 5$ ．若点P是矩形ABCD边上一点，且与点A，E构成以AE为腰的等腰三角形，则等腰三角形AEP的底边长是．

查看试题解析

三、解答题

13. 用适当的方法解下列方程：

(1)、 $x^{2} - 5 x + 6 = 0$

(2)、 $3 x^{2} - x - 1 = 0$

查看试题解析
14. 已知关于x的一元二次方程 $x^{2} + 3 x + k - 2 = 0$ 有实数根．

(1)、求实数k的取值范围．

(2)、设方程的两个实数根分别为 $x_{1} ， x_{2}$ ，若 $(x_{1} + 1) (x_{2} + 1) = - 1$ ，求k的值．

查看试题解析
15. 已知四边形 $A B C D$ 为矩形.点E是边 $A D$ 的中点.请仅用无刻度的直尺完成下列作图，不写作法，保留作图痕迹.

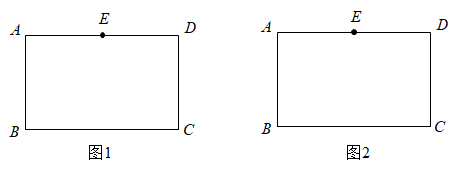(1)、在图1中作出矩形 $A B C D$ 的对称轴m，使 $m ∥ A B$ ；

(2)、在图2中作出矩形 $A B C D$ 的对称轴n：使 $n ∥ A D$ .

查看试题解析
16. 如图：点D在△ABC的边AB上，连接CD，∠1＝∠B，AD＝4，AC＝6，求AB的长．

查看试题解析
17. 如图，已知四边形ABCD是正方形，G为线段AD上任意一点， $C E ⊥ B G$ 于点E， $D F ⊥ C E$ 于点F.求证： $D F = B E + E F$ .

查看试题解析
18. 如图，在矩形 $A B C D$ 中， $E$ 为 $C D$ 边上一点，把 $△ A D E$ 沿 $A E$ 翻折，使点 $D$ 恰好落在 $B C$ 边上的点 $F$ 处．

(1)、求证： $△ A B F ∽ △ F C E$ ；

(2)、若 $A B = 3 \sqrt{3} ， A D = 6$ ，求 $E C$ 的长；

查看试题解析
19. 2022年冬奥会吉祥物冰墩墩深受人们喜爱，冬奥会特许商店将进货价为每个30元的冰墩墩饰品以40元的价格售出，平均每月能售出600个，调查表明：这种冰墩墩饰品的售价每上涨1元，其销售量就减少10个，同时规定售价在40-60元范围内．

(1)、当售价上涨x元时，销售量为个；

(2)、为了实现销售这种饰品平均每月10000元的销售利润，每个饰品应定为多少元？这时售出冰墩墩饰品多少个？

查看试题解析
20. 已知△ABC中，∠ACB＝90°，AC＝BC＝4cm，点P从点A出发，沿AB方向以每秒 $\sqrt{2}$ cm的速度向终点B运动，同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，设运动的时间为t秒．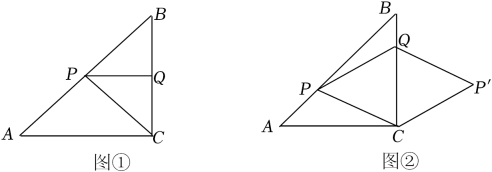

(1)、如图①，若PQ⊥BC，求t的值；

(2)、如图②，将△PQC沿BC翻折至△P′QC，当t为何值时，四边形QPCP′为菱形？

查看试题解析
21. 为了有效落实“双减”政策，某校随机抽取部分学生，开展了“书面作业完成时间”问卷调查．根据调查结果，绘制了如下不完整的统计图表：
频数分布统计表
组别
时间 $x （$ 分钟 $）$
频数
$A$
$0 \leq x < 20$
6
$B$
$20 \leq x < 40$
14
$C$
$40 \leq x < 60$
$m$
$D$
$60 \leq x < 80$
$n$
$E$
$80 \leq x < 100$
4
根据统计图表提供的信息解答下列问题：

(1)、频数分布统计表中的 $m =$ ▲ ， $n =$ ▲ ；并补全频数分布直方图；

(2)、已知该校有1000名学生，估计书面作业完成时间在60分钟以上(含60分钟)的学生有多少人？

(3)、若 $E$ 组有两名男同学、两名女同学，从中随机抽取两名学生了解情况，请用列表或画树状图的方法，求出抽取的两名同学恰好是一男一女的概率．

查看试题解析
22. 下面图片是八年级教科书中的一道题：如图，四边形 $A B C D$ 是正方形，点 $E$ 是边 $B C$ 的中点， $∠ A E F = 90 °$ ，且 $E F$ 交正方形外角的平分线 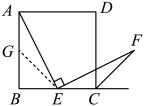$C F$ 于点 $F$ ．求证 $A E = E F$ ．（提示：取 $A B$ 的中点 $G$ ，连接 $E G$ ．）

(1)、请你思考题中“提示”，这样添加辅助线的意图是得到条件：；

(2)、如图1，若点 $E$ 是 $B C$ 边上任意一点（不与 $B$ 、 $C$ 重合），其他条件不变．求证： $A E = E F$ ；

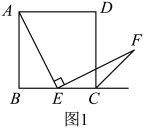(3)、在（2）的条件下，连接 $A C$ ，过点 $E$ 作 $E P ⊥ A C$ ，垂足为 $P$ ．设 $\frac{B E}{B C} = k$ ，当 $k$ 为何值时，四边形 $E C F P$ 是平行四边形，并给予证明．

查看试题解析
23. 阅读材料：小明喜欢探究数学问题，一天杨老师给他这样一个几何问题：
如图， $△ A B C$ 和 $△ B D E$ 都是等边三角形，点 $A$ 在 $D E$ 上.
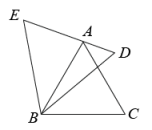
求证：以 $A E$ 、 $A D$ 、 $A C$ 为边的三角形是钝角三角形.

(1)、【探究发现】小明通过探究发现：连接 $D C$ ，根据已知条件，可以证明 $D C = A E$ ， $∠ A D C = 120 °$ ，从而得出 $△ A D C$ 为钝角三角形，故以 $A E$ 、 $A D$ 、 $A C$ 为边的三角形是钝角三角形.
请你根据小明的思路，写出完整的证明过程.

(2)、【拓展迁移】如图，四边形 $A B C D$ 和四边形 $B G F E$ 都是正方形，点 $A$ 在 $E G$ 上.
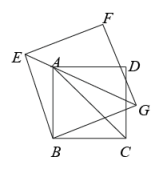
①试猜想：以 $A E$ 、 $A G$ 、 $A C$ 为边的三角形的形状，并说明理由.
②若 $A E^{2} + A G^{2} = 10$ ，试求出正方形 $A B C D$ 的面积.

查看试题解析

组别	时间 $x （$ 分钟 $）$	频数
$A$	$0 \leq x < 20$	6
$B$	$20 \leq x < 40$	14
$C$	$40 \leq x < 60$	$m$
$D$	$60 \leq x < 80$	$n$
$E$	$80 \leq x < 100$	4