广东省中山市2022-2023学年九年级上学期11月期中测试数学试题

试卷更新日期：2022-11-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，是一元二次方程的是（）

A、 $x - 1 = 0$ B、 $x^{2} - 3 = 0$ C、 $x^{2} + \frac{1}{x} = 1$ D、 $x + y = 2$

查看试题解析
2. 若m是方程 $x^{2} - x - 1 = 0$ 的一个根，则 $m^{2} - m + 2020$ 的值为（）

A、2019 B、2020 C、2021 D、2022

查看试题解析
3. 方程 ${(x - 3)}^{2} = 4$ 的根为（）

A、 $x_{1} = x_{2} = 5$ B、 $x_{1} = 5$ ， $x_{2} = 1$ C、 $x_{1} = x_{2} = 1$ D、 $x_{1} = 7$ ， $x_{2} = - 1$

查看试题解析
4. 把函数 $y = x^{2}$ 的图象向下平移1个单位，所得函数表达式为（）

A、 $y = x^{2} - 1$ B、 $y = {(x + 1)}^{2}$ C、 $y = x^{2} + 1$ D、 $y = {(x - 1)}^{2}$

查看试题解析
5. 已知函数 $y = (m + 3) x^{2} + 1$ 是二次函数，则m的取值范围为（）

A、 $m > - 3$ B、 $m < - 3$ C、 $m \neq - 3$ D、任意实数

查看试题解析
6. 《九章算术》中有一道“折竹抵地”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：如图，一根竹子原高1丈（1丈=10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？若设折断处离地面x尺，则下面所列方程正确的是（）

A、 $x^{2} + 3^{2} = (1 - x)^{2}$ B、 $x^{2} + (1 - x)^{2} = 3^{2}$ C、 $x^{2} + (10 - x)^{2} = 3^{2}$ D、 $x^{2} + 3^{2} = (10 - x)^{2}$

查看试题解析
7. 若关于 $x$ 的一元二次方程 $x^{2} + x + m = 0$ 有实数根，则m的最大整数值是（）

A、-1 B、0 C、1 D、2

查看试题解析
8. 关于二次函数y=-(x+2)²-1，下列说法错误的是（）

A、图象开口向下 B、图象顶点坐标是(-2，-1) C、当x＞0时，y随x增大而减小 D、图象与x轴有两个交点

查看试题解析
9. 若二次函数 $y = (m - 2) x^{2} + 2 x - 1$ 的图象有最低点，则m的取值范围是（）

A、 $m \geq 2$ B、 $m \leq 2$ C、 $m > 2$ D、 $m < 2$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则点 $A (a c ， b + c)$ 落在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析

二、填空题

11. 一元二次方程 $x^{2} - 2 x = 0$ 的较小实数根是．

查看试题解析
12. 若 $x^{2} - 4 x + a = (x - 2)^{2} - 1$ 成立，则 $a$ 的值为．

查看试题解析
13. 抛物线 $y = - 3 x^{2} + 2 x - 1$ 的图象与x轴交点的个数是．

查看试题解析
14. 某公司3月份的利润为200万元，5月份的利润为242万元，则平均每月利润的增长率是．

查看试题解析
15. 若点 $A (- 2 ， y_{1}) ， B (- 1 ， y_{2}) ， C (1 ， y_{3})$ 都在二次函数 $y = {(x + 2)}^{2} - c$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为．（用“<”连接）

查看试题解析
16. 如图，正方形的边长为4，以正方形中心为原点建立平面直角坐标系，作出函数 $y = \frac{1}{3} x^{2}$ 与 $y = - \frac{1}{3} x^{2}$ 的图象，则阴影部分的面积是．

查看试题解析
17. 某景点的“喷水巨龙”口中C处的水流呈抛物线形，该水流喷出的高度 $y (m)$ 与水平距离 $x (m)$ 之间的有关系如图所示，D为该水流的最高点， $D A ⊥ O B$ ，垂足为A．已知 $O C = O B = 8 m$ ， $O A = 2 m$ ，则该水流距水平面的最大高度AD的为m．

查看试题解析

三、解答题

18. 解方程： $x^{2} - 3 x - 2 = 0$ .

查看试题解析
19. 已知抛物线 $y = a x^{2}$ 经过点A(－2，－8).

(1)、求a的值，

(2)、若点P(m，－6)在此抛物线上，求点P的坐标.

查看试题解析
20. 二次函数 $y = a x^{2} + b x + 5$ 的图象经过 $(- 1 ， 11)$ ， $(1 ， 3)$ 两点．求这个二次函数的解析式并写出图象的对称轴和顶点．

查看试题解析
21. 定义：若一个一元二次方程的“某一个根”是另一个一元二次方程的一个根，则称这两个方程为“友好方程”．已知关于 $x$ 的一元二次方程 $x^{2} = 3 x$ 与 $x^{2} - 2 x + m - 1 = 0$ 是“友好方程”，求 $m$ 的值．

查看试题解析
22. 如图，在平面直角坐标系中，二次函数 $y = a x^{2} + 4 x - 6$ 的图象顶点是A，与x轴交于B，C两点，与y轴交于点D．其中点B的坐标是 $（ 2 ， 0 ）$ ．

(1)、求A，C两点的坐标，并根据图象直接写出当 $y < 0$ 时x的取值范围．

(2)、平移该二次函数的图象，使点D恰好落在点A的位置上，求平移后图象所对应的二次函数的表达式．

查看试题解析
23. 已知 $a$ 、 $b$ 、 $c$ 是 $△ A B C$ 的三边长，关于 $x$ 的一元二次方程 $(a + c) x^{2} + 2 b x + a - c = 0$ 有两个相等的实数根．

(1)、请判断 $△ A B C$ 的形状；

(2)、当 $a = 5$ ， $b = 3$ 时，求一元二次方程的解．

查看试题解析
24. 为进一步落实“双减增效”政策，某校增设活动拓展课程——开心农场．如图，准备利用现成的一堵“L”字形的墙面（粗线ABC表示墙面，已知 $A B ⊥ B C$ ， $A B = 3$ 米， $B C = 1$ 米）和总长为14米的篱笆围建一个“日”字形的小型农场DBEF（细线表示篱笆，小型农场中间GH也是用篱笆隔开），点D可能在线段AB上（如图1），也可能在线段BA的延长线上（如图2），点E在线段BC的延长线上．

(1)、当点D在线段AB上时，
①设DF的长为x米，请用含x的代数式表示EF的长；
②若要求所围成的小型农场DBEF的面积为12平方米，求DF的长；

(2)、DF的长为多少米时，小型农场DBEF的面积最大?最大面积为多少平方米?

查看试题解析
25. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + 2 a x + 4$ 与x轴交于点 $A (- 4.0)$ ， $B (x_{2} ， 0)$ ，与y轴交于点C．经过点B的直线 $y = k x + b$ 与y轴交于点 $D (0 ， 2)$ ，与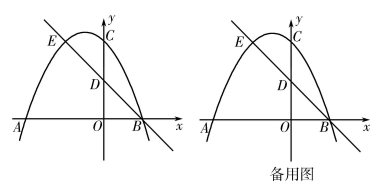抛物线交于点E．

(1)、求抛物线的表达式及B，C两点的坐标；

(2)、若点P为抛物线的对称轴上的动点，当△AEP的周长最小时，求点P的坐标；

(3)、若点M是直线BE上的动点，过M作 $M N ∥ y$ 轴交抛物线于点N，判断是否存在点M，使以点M，N，C，D为顶点的四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由．

查看试题解析