广东省深圳市福田区2022-2023学年九年级上学期期中测试数学试卷
试卷更新日期:2022-11-21 类型:期中考试
一、单选题
-
1. 在四边形ABCD是菱形,其中AB=4cm,则四边形ABCD的周长是( )A、5cm B、8cm C、12cm D、16cm2. 在▱ABCD中,E、F分别是AB、CD的中点,连接AF、CE.连接AC,当CA=CB时,判断四边形AECF是( )
 A、平行四边形 B、矩形 C、菱形 D、正方形3. 已知:是关于的一元二次方程,则m的值是( )A、1 B、2 C、3 D、44. 某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了3540张相片,如果全班有x名学生,根据题意,列出方程为( )A、 B、 C、 D、5. 一个密闭不透明的盒子里有若干个白球,在不许将球倒出来数的情况下,为了估计白球数,小刚向其中放入了8个黑球,搅匀后从中随意摸出一个球记下颜色,再把它放回盒中,不断重复这一过程,共摸球400次,其中80次摸到黑球,你估计盒中大约有白球( )A、32个 B、36个 C、40个 D、42个6. 为做好疫情防控工作,某学校门口设置了 , 两条体温快速检测通道,该校同学王明和李强均从通道入校的概率是( )A、 B、 C、 D、7. 若 , 则的值为( )A、 B、 C、 D、8. 已知ABC∽A1B1C1 , 且= . 若ABC的面积为4,则A1B1C1的面积是( )A、 B、6 C、9 D、189. 如图,在矩形中, , , 点E、F分别为、的中点,、相交于点G,过点E作 , 交于点H,则线段的长度是( )
A、平行四边形 B、矩形 C、菱形 D、正方形3. 已知:是关于的一元二次方程,则m的值是( )A、1 B、2 C、3 D、44. 某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了3540张相片,如果全班有x名学生,根据题意,列出方程为( )A、 B、 C、 D、5. 一个密闭不透明的盒子里有若干个白球,在不许将球倒出来数的情况下,为了估计白球数,小刚向其中放入了8个黑球,搅匀后从中随意摸出一个球记下颜色,再把它放回盒中,不断重复这一过程,共摸球400次,其中80次摸到黑球,你估计盒中大约有白球( )A、32个 B、36个 C、40个 D、42个6. 为做好疫情防控工作,某学校门口设置了 , 两条体温快速检测通道,该校同学王明和李强均从通道入校的概率是( )A、 B、 C、 D、7. 若 , 则的值为( )A、 B、 C、 D、8. 已知ABC∽A1B1C1 , 且= . 若ABC的面积为4,则A1B1C1的面积是( )A、 B、6 C、9 D、189. 如图,在矩形中, , , 点E、F分别为、的中点,、相交于点G,过点E作 , 交于点H,则线段的长度是( )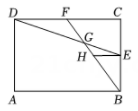 A、 B、1 C、 D、10. 如图,正方形 的边长为 , 在正方形外, ,过 作 于 ,直线 , 交于点 ,直线 交直线 于点 ,则下列结论正确的是( )
A、 B、1 C、 D、10. 如图,正方形 的边长为 , 在正方形外, ,过 作 于 ,直线 , 交于点 ,直线 交直线 于点 ,则下列结论正确的是( )
① ;② ;③ ;
④若 ,则
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 一元二次方程的一般形式为 .12. 已知m是方程的一个根,则代数式的值等于 .13. 如图,已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=8,BD=3,则DF的值是 .
 14. 如图所示.在矩形中, , 则度.
14. 如图所示.在矩形中, , 则度.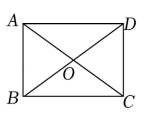 15. 如图,矩形中, , 交于E、F,则的最小值是 .
15. 如图,矩形中, , 交于E、F,则的最小值是 .
三、解答题
-
16. 用适当的方法解下列方程:(1)、;(2)、 .17. 已知关于x的一元二次方程有两个实数根.(1)、求k的取值范围;(2)、k取最大整数时求方程的根.18. 为落实“双减”政策,某校随机调查了50名学生平均每天完成书面作业所需时间的情况,根据调查数据绘制了如下不完整的统计图:(1)、补全条形统计图:
分组
时间x(时)
A
B
C
D
E
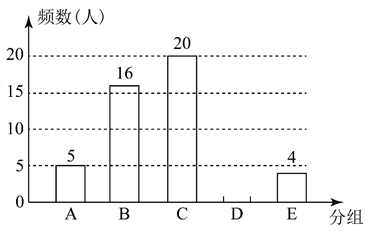 (2)、若该校有学生2000人,估计每天完成书面作业的时间不足1.5小时的学生有人.(3)、学校需要深入了解影响作业时间的因素,现从E组的4人中随机抽取2人进行谈话,已知E组中七、八年级各1人,九年级2人,则抽取的2人都是九年级学生的概率为多少?请用列表法或树状图说明.19. 如图,在四边形中, , 对角线交于点O,平分 , 过点C作交的延长线于点E,连接 .
(2)、若该校有学生2000人,估计每天完成书面作业的时间不足1.5小时的学生有人.(3)、学校需要深入了解影响作业时间的因素,现从E组的4人中随机抽取2人进行谈话,已知E组中七、八年级各1人,九年级2人,则抽取的2人都是九年级学生的概率为多少?请用列表法或树状图说明.19. 如图,在四边形中, , 对角线交于点O,平分 , 过点C作交的延长线于点E,连接 . (1)、求证:四边形是菱形;(2)、若 , 则的面积为 .20. 某快餐店有A、B两种招牌套餐,A套餐的成本为10元/份,B套餐成本为12元/份,一份B套餐的售价比一份A套餐的售价贵3元钱,买6份A套餐与买5份B套餐花费一样.(1)、求快餐店A套餐和B套餐的单价分别为多少元;(2)、商家统计发现,每天平均可售A套餐300份和B套餐200份,如果将A套餐的单价每提高0.1元,则每天将少售出A套餐5份:如果将B套餐的单价每提高0.2元,则每天将少售出B套餐7份;该快餐店决定将两种套餐都提高a元,在不考虑其他因素的条件下,当a为多少时,才能使该商家每天销售这两种套餐获取的利润共2055元.21. 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.如图, , 四边形是损矩形,则该损矩形的直径是线段 . 同时我们还发现损矩形中有公共边的两个三角形角的特点:在公共边的同侧的两个角是相等的.如图中:和有公共边 , 在同侧有和 , 此时;再比如和有公共边 , 在同侧有和 , 此时 .
(1)、求证:四边形是菱形;(2)、若 , 则的面积为 .20. 某快餐店有A、B两种招牌套餐,A套餐的成本为10元/份,B套餐成本为12元/份,一份B套餐的售价比一份A套餐的售价贵3元钱,买6份A套餐与买5份B套餐花费一样.(1)、求快餐店A套餐和B套餐的单价分别为多少元;(2)、商家统计发现,每天平均可售A套餐300份和B套餐200份,如果将A套餐的单价每提高0.1元,则每天将少售出A套餐5份:如果将B套餐的单价每提高0.2元,则每天将少售出B套餐7份;该快餐店决定将两种套餐都提高a元,在不考虑其他因素的条件下,当a为多少时,才能使该商家每天销售这两种套餐获取的利润共2055元.21. 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.如图, , 四边形是损矩形,则该损矩形的直径是线段 . 同时我们还发现损矩形中有公共边的两个三角形角的特点:在公共边的同侧的两个角是相等的.如图中:和有公共边 , 在同侧有和 , 此时;再比如和有公共边 , 在同侧有和 , 此时 . (1)、请在图中找出一对这样的角来:;(2)、如图,中, , 以为一边向外作菱形 , D为菱形对角线的交点,连接 .
(1)、请在图中找出一对这样的角来:;(2)、如图,中, , 以为一边向外作菱形 , D为菱形对角线的交点,连接 .①四边形 ▲ 损矩形(填“是”或“不是”);
②当平分时,判断四边形为何种特殊的四边形?请说明理由;
③若 , 求的长.
22. 如图,在中, , D、E分别是的中点,连接 . 点P从点D出发,沿方向匀速运动,速度为;同时,点Q从点B出发,沿方向匀速运动,速度为 , 当点P停止运动时,点Q也停止运动.连接 , 设运动时间为 . 解答下列问题: (1)、cm,(用含有t的代数式表示)(2)、请求出t为何值时,以点E、P、Q为顶点的三角形与相似?(3)、当t为何值时,为等腰三角形?(直接写出答案即可).
(1)、cm,(用含有t的代数式表示)(2)、请求出t为何值时,以点E、P、Q为顶点的三角形与相似?(3)、当t为何值时,为等腰三角形?(直接写出答案即可).