广东省梅州市五华县2022-2023学年九年级上学期期中考试数学试题

试卷更新日期：2022-11-21 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程 $2 x^{2} - 5 x + 1 = 0$ 的一次项系数是（）

A、-5 B、0 C、1 D、2

查看试题解析
2. 矩形具有而菱形不一定具有的性质是（）

A、对角线互相平分 B、对角线相等 C、邻边相等 D、对角线互相垂直

查看试题解析
3. 若m、n是关于x的方程 $x^{2} + 2 x - 3 = 0$ 的两个根，则 $\frac{1}{m} + \frac{1}{n}$ 的值为（）

A、 $\frac{3}{2}$ B、 $- \frac{1}{2}$ C、 $\frac{2}{3}$ D、 $- \frac{2}{3}$

查看试题解析
4. 如图，四边形 $A B C D$ 是正方形，延长 $A B$ 到点 $E$ ，使 $A E = A C$ ，则 $∠ B C E$ 的度数是（）

A、 $62.5 °$ B、 $45 °$ C、 $32.5 °$ D、 $22.5 °$

查看试题解析
5. 2022年北京冬奥会吉祥物“冰墩墩”意喻敦厚、健康、活泼、可爱，象征着冬奥会运动员强壮的身体、坚韧的意志和鼓舞人心的奥林匹克精神，随着北京冬奥会开幕日的临近，某特许零售店“冰墩墩”的销售日益火爆，据统计，该店2021年第四季度的“冰墩墩”总销售额为9.93万件，其中10月的销量为3万件，设11，12月份的平均增长率为 $x$ ，则可列方程为 $($ $)$

A、 $3 {(1 + x)}^{2} = 9.93$ B、 $3 + 3 {(1 + x)}^{2} = 9.93$ C、 $3 + 3 x + 3 {(1 + x)}^{2} = 9.93$ D、 $3 + 3 (1 + x) + 3 {(1 + x)}^{2} = 9.93$

查看试题解析
6. “二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界普为“中国第五大发明”，小文购买了“二十四节气”主题邮票，他要将“立春”“立夏”“秋分”“大暑”四张邮票中的两张送给好朋友小乐．小文将它们背面朝上放在桌面上（邮票背面完全相同），让小乐从中随机抽取一张（不放回），再从中随机抽取一张，则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看试题解析
7. 如图，在矩形ABCD中，BC=20cm，点P和点Q分别从点B和点D同时出发，按逆时针方向沿矩形ABCD的边运动，点P和点Q的速度分别为3cm/s和2cm/s，当四边形ABPQ初次为矩形时，点P和点Q运动的时间为（）秒．

A、2 B、3 C、4 D、5

查看试题解析
8. 【教材呈现】下图是北师大版九年级上册数学教材第25页第4题内容的变式．如图，三个边长相同的正方形重叠在一起， $O_{1}$ 、 $O_{2}$ 是其中两个正方形的中心，阴影部分的面积和是8，则正方形的边长为（）

A、2 B、4 C、8 D、 $2 \sqrt{2}$

查看试题解析
9. 对于实数a，b定义运算“ $\otimes$ ”为 $a \otimes b = b^{2} - a b$ ，例如 $3 \otimes 2 = 2^{2} - 3 \times 2 = - 2$ ，则关于x的方程 $(m + 2) \otimes x = 1 - m$ 的根的情况，下列说法正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
10. 如图，在矩形 $A B C D$ 中，点E是对角线 $A C$ 上一点，有 $A E = A B = \sqrt{3} B C$ 且 $B C = a$ ，点P是 $B E$ 上一动点，则点P到边 $A B$ ， $A C$ 的距离之和 $P M + P N$ 的值（）

A、有最大值a B、有最小值 $\frac{\sqrt{3}}{2} a$ C、是定值 $\frac{1}{2} a$ D、是定值 $\frac{\sqrt{3}}{2} a$

查看试题解析

二、填空题

11. 一元二次方程 $2 x^{2} = 8 x$ 的根．

查看试题解析
12. 已知菱形 $A B C D$ 的对角线 $A C = 4$ ， $B D = 5$ ，则菱形 $A B C D$ 的面积为．

查看试题解析
13. 如图是小明的健康绿码示意图，用黑白打印机打印于边长为 $3 m$ 的正方形区域内，为了估计图中黑色部分的总面积，在正方形区域内随机掷点，经过大量重复试，发现点落入黑色部分的频率稳定在 $0.6$ 左右，据此可以估计黑色部分的总面积约为 $c m^{2}$ ．

查看试题解析
14. 代数式 $a^{2} - 6 a + 13$ 可化为 $a^{2} - 6 a + 9 + 4 = {(a - 3)}^{2} + 4$ ；无论a取何值 ${(a - 3)}^{2} \geq 0$ ，所以 ${(a - 3)}^{2} + 4 \geq 4$ ，即 ${(a - 3)}^{2} + 4$ 有最小值为4．仿照上述思路，代数式 $- a^{2} + 4 a - 8$ 的最大值为．

查看试题解析
15. 如图，在正方形 $A B C D$ 中， $A B = 6 \sqrt{2}$ ． E、F分别为边 $A B 、 B C$ 的中点，连接 $A F 、 D E$ ，点N、M分别为 $A F 、 D E$ 的中点，连接 $M N$ ，则 $M N$ 的长度为．

查看试题解析

三、解答题

16. 解方程： $5 x^{2} - 3 x - 2 = 0$ ；

查看试题解析
17. 如图，四边形 $A B C D$ 是菱形， $A E ⊥ C D$ 于点E， $A F ⊥ B C$ 于点F．求证： $C E = C F$ ．

查看试题解析
18. 2022年我国已成为全球最大的电动汽车市场，电动汽车在保障能源安全，改善空气质量等方面较传统汽车都有明显优势，某汽车 $4 S$ 店销售某种型号的电动汽车，每辆进货价为19万元，该店经过一段时间的市场调研发现：当销售价为25万元时，平均每月能售出18辆，而当销售价每降低 $0.5$ 万元时，平均每月能多售出3辆．该 $4 S$ 店要想平均每月的销售利润为120万元，并且使成本尽可能的低，则每辆汽车应降价多少万元？

查看试题解析
19. 2022年10月12日16：01，“天宫课堂”第三课在中国空间站开讲，神舟十四号航天员陈冬、刘洋、蒸旭哲作为“太空教师”，为广大青少年再度带来了又一堂精彩绝伦的太空科普课，航天员老师分别为大家演示了微重力环境下毛细效应实验、水球变“懒”实验、太空趣味饮水以及旋转类演示实验“会调头的扳手”，小明的物理老师组织全班同学开展“我爱科学”活动，分享观看四个实验后的感想．老师将四个实验的名称分别写在四张完全相同的卡片上，背面朝上，每位同学随机抽取一张，做好记录后放回，并向同伴分享对应实验的观看收获．

(1)、小明抽到写有“会调头的扳手”卡片，并分享观后收获的概率为；

(2)、通过列表或树状图，求出小明和同桌小华恰好都抽到写有“会调头的扳手”卡片，并分享观后收获的概率．

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} + (2 m - 1) x + m^{2} - 1 = 0$ ．

(1)、若方程有实数根，求实数m的取值范围；

(2)、若方程两实数根分别为 $x_{1} ， x_{2}$ ，且满足 $x_{1}^{2} + x_{2}^{2} = 9$ ，求实数m的值．

查看试题解析
21. 如图，在平行四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O， $B E ∥ A C$ 交 $D C$ 的延长线于点E， $B D = B E$ ．

(1)、求证：四边形 $A B C D$ 是矩形；

(2)、若 $∠ A D B = 30 °$ ， $A C = 2$ ，求矩形 $A B C D$ 的面积．

查看试题解析
22. 配方法是数学中重要的一种思想方法．它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题．我们定义：一个整数能表示成 $a^{2} + b^{2}$ （a、b是整数）的形式，则称这个数为“完美数”．例如，5是“完美数”．理由：因为 $5 = 2^{2} + 1^{2}$ ，所以5是“完美数”．

(1)、解决问题：
已知10是“完美数”，请将它写成 $a^{2} + b^{2}$ （a、b是整数）的形式；

(2)、若 $x^{2} - 4 x + 3$ 可配方成 ${(x - m)}^{2} + n$ （m、n为常数），则 $m n =$ ；

(3)、探究问题：
已知 $x^{2} + y^{2} - 2 x + 6 y + 10 = 0$ ，则 $x + y =$ ；

(4)、已知 $S = x^{2} + 9 y^{2} + 4 x - 12 y + k$ （x、y是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由．

(5)、拓展结论：
已知实数x、y满足 $- x^{2} + \frac{7}{3} x + y - 2 = 0$ ，求 $5 x - 3 y$ 的最值．

查看试题解析
23. 如图，矩形 $A B C D$ 中， $A B = 2$ ，点E、F、G、H，分别是 $B C 、 C D 、 A D 、 A B$ 上的动点（顶点除外），若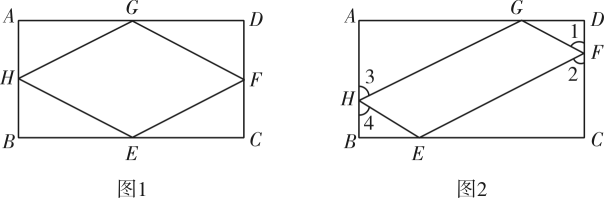 $∠ 1 = ∠ 2 = ∠ 3 = ∠ 4$ ；

(1)、在图1中，点E，F，G，H分别是 $B C ， C D ， A D ， A B$ 上的中点．
①判断四边形 $E F G H$ 的形状，并证明；
②当四边形 $E F G H$ 是正方形时，求它的周长；

(2)、在图2中，已知 $B C = 4$ ，判断四边形 $E F G H$ 的周长是否会随着点G的变化而变化，如不变化，求出其周长，若会变化，说明理由；

查看试题解析