广东省河源市紫金县2022-2023学年九年级上学期期中考试数学试题

试卷更新日期：2022-11-21 类型：期中考试

进入出卷网下载

一、单选题

1. 已知 $\frac{x}{y} = \frac{3}{5}$ ，则下列式子成立的是（）

A、 $5 x = 3 y$ B、 $x y = 15$ C、 $\frac{5}{y} = \frac{x}{3}$ D、 $3 x = 5 y$

查看试题解析
2. 顺次连接矩形四边中点所得的四边形一定是（）

A、正方形 B、矩形 C、菱形 D、等腰梯形

查看试题解析
3. 下列对一元二次方程x²+x﹣3=0根的情况的判断，正确的是（）

A、有两个不相等实数根 B、有两个相等实数根 C、有且只有一个实数根 D、没有实数根

查看试题解析
4. 同时抛掷两枚均匀的硬币，落地后两枚硬币都是正面朝上的概率是（）

A、 $1$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
5. 用配方法解方程 $x^{2} - 4 x - 7 = 0$ 时，原方程应变形为（）

A、 ${(x - 2)}^{2} = 11$ B、 ${(x + 2)}^{2} = 11$ C、 ${(x - 4)}^{2} = 23$ D、 ${(x + 4)}^{2} = 23$

查看试题解析
6. 如图，四边形ABCD是菱形，AC＝8，DB＝6，DH⊥AB于H，则DH等于（）

A、 $\frac{24}{5}$ B、 $\frac{12}{5}$ C、5 D、4

查看试题解析
7. 在一个不透明的口袋中，装有若干个红球和4个黄球，它们除颜色外没有任可其他区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球实验发现，摸到黄球的频率是0.2，则估计盒子中大约有红球（）

A、16个 B、20个 C、25个 D、30个

查看试题解析
8. 为执行“两免一补”政策，某地区2006年投入教育经费2500万元，预计2008年投入3600万元．设这两年投入教育经费的年平均增长百分率为x，则下列方程正确的是（　　）

A、2500x²=3600 B、2500（1+x）²=3600 C、2500（1+x%）²=3600 D、2500（1+x）+2500（1+x）²=3600

查看试题解析
9. 如图，将矩形ABCD沿EF折叠，使顶点C恰好落在边AB上的点C′上，且GE＝GC′，若DE＝3，AB＝6，BC＝9，则BF的长为（）

A、4 B、3 $\sqrt{2}$ C、4.5 D、5

查看试题解析
10. 正方形ABCD，正方形CEFG如图放置，点B，C，E在同一条直线上，点P在BC边上，PA＝PF，且∠APF＝90°，连接AF交CD于点M.有下列结论：①EC＝BP；②AP＝AM：③∠BAP＝∠GFP；④AB²+CE²＝ $\frac{1}{2}$ AF²；⑤S_正方形_ABCD+S_正方形_CGFE＝2S_△_APF ，其中正确的是（　　）

A、①②③ B、①③④ C、①②④⑤ D、①③④⑤

查看试题解析

二、填空题

11. 已知四条线段4，x，2，3成比例，若x为整数，则x= ．

查看试题解析
12. 经过某十字路口的汽车，可直行，也可向左转或向右转，如果这三种可能性大小相同，则两辆汽车经过该十字路口时都直行的概率是．

查看试题解析
13. 如图，在三角形ABC中， $D E ∥ B C$ ， $A D = 2 ， A B = 6 ， A E = 3$ ，则 $A C$ 的长为．

查看试题解析
14. 已知关于x的一元二次方程 $x^{2} - 2 x + 1 = 0$ 的两个不相等的实数根分别为 $x_{1}$ ， $x_{2}$ ，那么 $x_{1} + x_{2} + x_{1} x_{2} =$ ．

查看试题解析
15. 如图，已知正方形ABCD的边长为5，点E、F分别在AD、DC上，AE=DF=2，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为．

查看试题解析

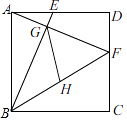
三、解答题

16. 解方程：x²﹣7x+10=0.

查看试题解析
17. 如图，在菱形ABCD中，AC＝8，BD＝6，求△ABC的周长.

查看试题解析
18. 如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB，BC各为多少米？

查看试题解析
19. 一个不透明的口袋里装有分别标有汉字“书”“香”“校”“园”的四个小球，除汉字不同之外，小球没有任何区别，每次摸前先搅拌均匀．

(1)、若从中任取一个球，球上的汉字刚好是“书”的概率为；

(2)、先从中任取一个球，不放回，再从中任取一个球，请用画树状图或列表的方法，求取出的两个球上的汉字能组成“书香”的概率．

查看试题解析
20. 如图，已知在▱ABCD中，对角线AC，BD交于点O，E是BD延长线上的点，且EA=EC．（8′）

(1)、求证：四边形ABCD是菱形；

(2)、若∠DAC=∠EAD+∠AED，求证：四边形ABCD是正方形．

查看试题解析
21. 某服装店在销售中发现：进货价为每件50元、销售价为每件90元的某品牌服装平均每天可售出20件，现商场决定采取适当的降价措施，扩大销售量，增加盈利．经市场调查发现：如果每件服装降价1元，那么平均每天就可多售出2件．设每件衣服降价x元．

(1)、现在每天卖出件（用含x的代数式表示）；

(2)、当x为何值时，平均每天销售的这种服装能盈利1200元且能使顾客得到较多的实惠？

查看试题解析
22. 矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为 $(6 ， 8)$ ， D是 $O A$ 的中点，点E在线段 $A B$ 上．

(1)、点D的坐标是；

(2)、求直线CD的解析式；

(3)、当 $△ C D E$ 的周长最小时，求点E的坐标．

查看试题解析
23. 如图，在长方形ABCD中，边AB、BC的长（AB＜BC）是方程x²-7x+12=0的两个根.点P从点A出发，以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动，运动时间为t（秒）.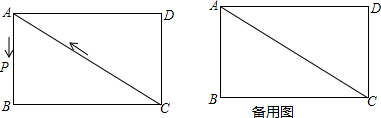

(1)、求AB与BC的长；

(2)、当点P运动到边BC上时，试求出使AP长为 $\sqrt{10}$ 时运动时间t的值；

(3)、当点P运动到边AC上时，是否存在点P，使△CDP是等腰三角形？若存在，请求出运动时间t的值；若不存在，请说明理由.

查看试题解析