广东省广州市海珠区2022-2023学年九年级上学期期中联考数学科试卷试题

试卷更新日期：2022-11-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，既是中心对称又是轴对称的图形是（）

A、 B、 C、 D、

查看试题解析
2. 下列函数中，二次函数是（）

A、 $y = - 4 x + 5$ B、 $y = x (x - 3)$ C、 $y = {(x + 4)}^{2} - x^{2}$ D、 $y = \frac{1}{x^{2}}$

查看试题解析
3. 用配方法解方程 $x^{2} - 4 x + 2 = 0$ ，下列配方正确的是（）

A、 $(x - 2)^{2} = 6$ B、 $(x + 2)^{2} = 2$ C、 $(x - 2)^{2} = - 2$ D、 $(x - 2)^{2} = 2$

查看试题解析
4. 某种植基地2016年蔬菜产量为80吨，预计2018年蔬菜产量达到100吨，求蔬菜产量的年平均增长率，设蔬菜产量的年平均增长率为x，则可列方程为（）

A、80（1+x）²=100 B、100（1﹣x）²=80 C、80（1+2x）=100 D、80（1+x²）=100

查看试题解析
5. 抛物线y=（x+2）²﹣3可以由抛物线y=x²平移得到，则下列平移过程正确的是（）

A、先向左平移2个单位，再向上平移3个单位 B、先向左平移2个单位，再向下平移3个单位 C、先向右平移2个单位，再向下平移3个单位 D、先向右平移2个单位，再向上平移3个单位

查看试题解析
6. 关于二次函数 $y = - 3 x^{2} + 5$ ，下列说法中正确的是（）

A、图象的开口向上 B、当 $x > - 1$ 时， $y$ 随 $x$ 的增大而增大 C、图象的顶点坐标是 $(0 ， 5)$ D、当 $x = 0$ 时， $y$ 有最小值是5

查看试题解析
7. 函数 $y = k x^{2} - 6 x + 3$ 的图象与x轴有交点，则k的取值范围是（　　）

A、 $k < 3$ B、 $k < 3$ 且 $k \neq 0$ C、 $k \leq 3$ D、 $k \leq 3$ 且 $k \neq 0$

查看试题解析
8. 如图，在同一平面内，将△ABC绕A点逆时针旋转到△ADE的位置．若AC⊥DE ， ∠ABD＝62°，则∠ACB的度数为（）

A、56° B、44° C、34° D、40°

查看试题解析
9. 下列命题：① 若b＝a＋c时，一元二次方程 $a x^{2} + b x + c = 0$ 一定有实数根；② 若方程 $a x^{2} + b x + c = 0$ 有两个不相等的实数根，则方程 $c x^{2} + b x + a = 0$ 也一定有两个不相等实数根；③ 若二次函数 $y = a x^{2} + c$ ，当取 $x_{1}$ 、 $x_{2}$ （ $x_{1} \neq x_{2}$ ）时，函数值相等，则当x取 $x_{1} + x_{2}$ 时函数值为0；④ 若 $b^{2} - 4 a c > 0$ ，则二次函数 $y = a x^{2} + b x + c$ 的图像与坐标轴的公共点的个数是2或3，其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，已知 $△ A B C$ 的顶点坐标分别为 $A (0 ， 2)$ ， $B (1 ， 0)$ ， $C (2 ， 1)$ ，若二次函数 $y = x^{2} + 2 b x + 1$ 的图象与阴影部分（含边界）一定有公共点，则实数 $b$ 的取值范围是（）

A、 $b \leq - 1$ B、 $b \geq - 1$ C、 $b > - 1$ D、 $b < - 1$

查看试题解析

二、填空题

11. 直角坐标系中，点 $(3 ， 1)$ 绕原点顺时针旋转 $90 °$ 的对称点是．

查看试题解析
12. 已知函数 $y = (m - 2) x^{m^{2} - 2}$ 是二次函数，则m= ．

查看试题解析
13. 已知方程 $x^{2} - b x + 3 = 0$ 的一根为3，则方程的另一根为

查看试题解析
14. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ，已知 $∠ A D C = 150 °$ ，则 $∠ A O C$ 等于 $°$ .

查看试题解析
15. 抛物线 $y = x^{2} - 2 x - 3$ 的图象为 $G_{1}$ ， $G_{1}$ 关于 $x$ 轴对称的图象为 $G_{2}$ ， $G_{1}$ 和 $G_{2}$ 组成的图象与直线 $y = x + m$ 有3个公共点时， $m$ 的范围（或值）是．

查看试题解析
16. 已知，二次函数 $y = 4 x^{2} - 4 a x + a^{2} + 2 a + 2$ 在 $0 \leq x \leq 2$ 上有最小值4，则 $a =$ ．

查看试题解析

三、解答题

17. 解方程．

(1)、 $x^{2} - 4 x - 12 = 0$

(2)、 $4 x^{2} - 4 x - 3 = 0$

查看试题解析
18. 如图， $△ A B C$ 三个顶点的坐标分别为 $A (2 ， 4)$ ， $B (1 ， 1)$ ， $C (4 ， 3)$ ．

(1)、请画出 $△ A B C$ 关于原点 $O$ 中心对称的 $△ A_{1} B_{1} C_{1}$ ，并写出 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标；

(2)、请画出 $△ A B C$ 关于 $y$ 轴对称的 $△ A_{2} B_{2} C_{2}$ ，则 $△ A_{1} B_{1} C_{1}$ 与 $△ A_{2} B_{2} C_{2}$ 有什么位置关系?

查看试题解析
19. 如图，在 $⊙ O$ 中， $C P = 2$ ， $P D = 6$ ， $A P = 5$ ，弦 $C D ⊥ A B$ ，垂足为点 $P$ ，求 $O P$ 的长度．

查看试题解析
20. 如图，一次函数 $y = k x + b$ 与二次函数 $y = a x^{2}$ 的图象交于 $A (1 ， m)$ 和 $B (- 2 ， 4)$

(1)、直接写出两个函数的解析式；

(2)、点 $P$ 为直线 $A B$ 下方抛物线线上一个动点，过 $P$ 作 $P H ∥ y$ 轴与 $A B$ 交于 $H$ 点，当 $P H$ 为最大值时，求 $P$ 点坐标．

查看试题解析
21. 如图1，在一张长 $40 c m$ ，宽 $25 c m$ 的长方形硬纸片，裁去角上四个小正方形之后，折成如图2的无盖纸盒，若纸盒的底面积是 $450 c m^{2}$ ，则纸盒的高是多少？

查看试题解析
22. 已知抛物线： $y = x^{2} - 2 m x + m^{2} - 16$

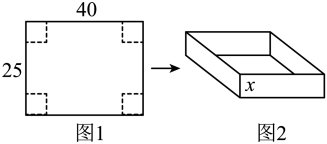(1)、求证：无论 $m$ 为何值，与 $x$ 轴总有两个不同的交点 $A$ ， $B$ ．

(2)、若 $(x_{A} - 1) (x_{B} - 1) = 9$ ，求 $m$ 的值．

(3)、若 $O A = 3 O B$ ，请直接写出 $m$ 的值．

查看试题解析
23. 某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．

(1)、求出每天的销售利润 $y$ （元）与销售单价 $x$ （元）之间的函数关系式，并求出自变量 $x$ 的取值范围；

(2)、如果该企业每天的总成本不超过7000元，那么销售单价为多少元时，每天的销售利润最大？最大利润是多少？（每天的总成本=每件的成本×每天的销售量）

查看试题解析
24. 【阅读理解】
六中珠江中学初三数学学习小组，在做《圆》的课题学习探究时发现：
三角形有五心：重心、外心、内心、垂心、旁心，其中的外心、内心、旁心是我们现在学习的《圆》的“心”．而找“心”所用的工具“垂直平分线”和“角平分线”是8年级学习内容．小组同学做了以下摘要记录
重心：三角形三条中线的交点叫做三角形重心，它是力的平衡点，重心是中线的三等分点．
外心：三角形外接圆的圆心，外心为三角形三边的垂直平分线的交点，外心到三顶点距离相等．
内心：三角形内切圆的圆心，内心为三角形三条内角平分线的交点，内心到三角形三边距离相等．
【实践探究】

(1)、已知 $△ A B C$ 中， $A B = 20$ ， $A C = 13$ ， $B C = 21$
①作出 $△ A B C$ 的角平分线交点 $O$ （尺规作图，不写作法，保留作图痕迹）；
过 $O$ 作 $O M ⊥ B C$ ，垂足为 $M$ （不需尺规作图）；
以 $O$ 为圆心， $O M$ 为半径作出 $△ A B C$ 的内切圆
②求出 $△ A B C$ 的面积．
③求出内切圆 $⊙ O$ 的半径 $R$ 的长度．

(2)、已知 $△ A B C$ 中， $A B = 2 \sqrt{5}$ ， $A C = 4 \sqrt{2}$ ， $B C = 6$ ，
①作出 $△ A B C$ 的三边垂直平分线的交点 $O$ （尺规作图，不写作法，保留作图痕迹）；
连接 $A O$ ；以 $O$ 为圆心， $A O$ 为半径作出 $△ A B C$ 的外接圆
②以 $B$ 为原点， $B C$ 所在的直线为 $x$ 轴（点 $C$ 在点 $B$ 右方）建立直角坐标系，求点A坐标．
③求出外接圆 $⊙ O$ 的半径 $R$ 的长度．

查看试题解析
25. 已知抛物线y＝x²﹣mx﹣m﹣1与x轴交于A、B两点，点A在点B的左边，与y轴交于点C（0，﹣3）．

(1)、求点A、B的坐标；

(2)、点D是抛物线上一点，且∠ACO+∠BCD＝45°，求点D的坐标；

(3)、将抛物线向上平移m个单位，交线段BC于点M ， N ，若∠MON＝45°，求m的值．

查看试题解析