广东省佛山市南海区狮山镇2022-2023学年九年级上学期期中教学质量数学监测试题

试卷更新日期：2022-11-21 类型：期中考试

进入出卷网下载

一、单选题

1. 为做好疫情防控工作，某学校门口设置了 $A$ ， $B$ 两条体温快速检测通道，该校同学王明和李强均从 $A$ 通道入校的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
2. 已知 $\frac{b}{a} = \frac{3}{2}$ ，下列变形正确的是（）

A、 $a b = 6$ B、 $2 a = 3 b$ C、 $a = \frac{3}{2 b}$ D、 $3 a = 2 b$

查看试题解析
3. 把一元二次方程 $(x + 2) (x - 2) = x$ 化成一般形式，正确的是（）

A、 $x^{2} - x + 4 = 0$ B、 $x^{2} - x - 4 = 0$ C、 $x^{2} + x + 4 = 0$ D、 $x^{2} + x - 4 = 0$

查看试题解析
4. 若顺次连接四边形ABCD四边中点所得的四边形是正方形，则四边形ABCD一定满足（）

A、是正方形 B、AB＝CD且AB∥CD C、是矩形 D、AC＝BD且AC⊥BD

查看试题解析
5. 按照党中央、国务院决策部署，为了活跃市场主体、助推各地区经济发展，各省市地区抓紧推动稳经济一揽子政策落实落地．江夏区制定了“黄金十条”，坚定企业疫后发展信心，促进企业稳步高效增长.2022年我区某企业4月份的利润是100万元，第二季度的总利润达到500万元，设利润平均月增长率为x，则依题意列方程为（）

A、 $100 (1 + x)^{2} = 500$ B、 $100 (1 + x^{2}) = 500$ C、 $100 (1 + x) + 100 (1 + x)^{2} = 500$ D、 $100 + 100 (1 + x) + 100 (1 + x)^{2} = 500$

查看试题解析
6. 若关于 $x$ 的方程 $(a - 2) x^{2} - 2 x + 1 = 0$ 是一元二次方程，则（）

A、 $a \neq 2$ B、 $a \neq 0$ C、 $a = 2$ D、 $a = 0$

查看试题解析
7. 已知菱形ABCD中，对角线AC与BD交于点O，∠BAD＝120°，AC＝4，则该菱形的周长是（）

A、 $16 \sqrt{3}$ B、16 C、 $8 \sqrt{3}$ D、8

查看试题解析
8. 某学校要组织一次篮球比赛，赛制为单循环形式（每两队之间都要赛一场），计划安排21场比赛，设参赛队数为x，列方程为（）

A、x（x-1）＝21 B、 $\frac{1}{2}$ x（x-1）＝21 C、2x（x-1）＝21 D、x（x＋1）＝21

查看试题解析
9. 如图，木杆 $A B$ 斜靠在墙壁上， $P$ 是 $A B$ 的中点，当木杆的上端 $A$ 沿墙壁 $N O$ 竖直下滑时，木杆的底端 $B$ 也随之沿着射线 $O M$ 方向滑动，则下滑过程中 $O P$ 的长度变化情况是（）

A、逐渐变大 B、不断变小 C、不变 D、先变大再变小

查看试题解析
10. 如图，在正方形 $A B C D$ 中， $A B = 3$ ，点E，F分别在边 $A B ， C D$ 上， $∠ E F D = 60 °$ ，若将四边形 $E B C F$ 沿 $E F$ 折叠，点 $B^{'}$ 恰好落在 $A D$ 边上，则 $B E$ 的长度为（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析

二、填空题

11. 用配方法解方程 $x^{2} - 4 x - 3 = 0$ ，配方得 $(x + m)^{2} = 7$ ，常数m的值是．

查看试题解析
12. 某医院要从 $A$ ， $B$ ， $C$ 三名志愿者中任意抽调两人助力全民核酸检测工作，恰好抽到志愿者 $B$ 和 $C$ 的概率是．

查看试题解析
13. 若关于x的一元二次方程 $m x^{2} + x + 3 ＝ 0$ 有两个相等的实数根，则m的值为．

查看试题解析
14. 如图，在Rt△ABC中，∠C=90°，AC=12，BC=5，在三角形内挖掉正方形CDEF，则正方形CDEF的边长为．

查看试题解析
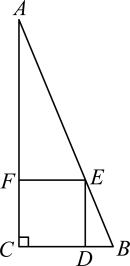15. 如图，E为边长为2 $\sqrt{2}$ 的正方形ABCD的对角线BD上的一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ+PR的值是．

查看试题解析

三、解答题

16. 用适当方法解方程： $2 {(x - 1)}^{2} - 18 = 0$

查看试题解析
17. 已知关于 $x$ 的一元二次方程 $m x^{2} + (m - 3) x - 3 = 0$ ．

(1)、求证：方程总有两个实数根；

(2)、若方程的两个根均为整数，求正整数 $m$ 的值．

查看试题解析
18. 如图，在平行四边形ABCD中，对角线AC，BD交于点O．M为AD中点，连接CM交BD于点N，且ON＝1

(1)、求证： $△ D M N ∽ △ B C N$ ；

(2)、求BD的长，

查看试题解析
19. 某游戏有个摸球的环节，现有四个分别标有数字4，-2，3，-1的小球，它们除数字外其余全部相同，现将它们放入一个不透明的布袋中，搅匀后从袋中随机地摸取一个不放回，将该小球上的数字记为a，再随机地摸取一个，将小球上的数字记为b．

(1)、请你用列表法或树状图（树形图）法给出（a，b）所有可能的结果；

(2)、求所选出的a，b能使坐标点（a，b）落在第二象限的概率．

查看试题解析
20. 2022年北京冬奥会吉祥物深受大家的喜欢．某特许零售店的冬奥会吉祥物销售量日益火爆．据统计，该店2022年1月的“冰墩墩”销量为2万件，2022年3月的“冰墩墩”销量为2.42万件．

(1)、求该店“冰墩墩”销量的月平均增长率；

(2)、该零售店4月将采用提高售价的方法增加利润，根据市场调研得出结论：如果将进价80元的“冰墩墩”按每件100元出售，每天可销售500件，在此基础上售价每涨1元，那么每天的销售量就会减少10件，该零售店要想每天获得12000元的利润，且销量尽可能大，则每件商品的售价应该定为多少元？

查看试题解析
21. 阅读以下文字并解决问题：对于形如 $x^{2} + 2 a x + a^{2}$ 这样的二次三项式，我们可以直接用公式法把它分解成 $(x + a)^{2}$ 的形式，但对于二次三项式 $x^{2} + 6 x - 27$ ，就不能直接用公式法分解了．此时，我们可以在 $x^{2} + 6 x - 27$ 中间先加上一项 $9$ ，使它与 $x^{2} + 6 x$ 的和构成一个完全平方式，然后再减去 $9$ ，则整个多项式的值不变．即： $x^{2} + 6 x - 27 = (x^{2} + 6 x + 9) - 9 - 27 = (x + 3)^{2} - 6^{2} = (x + 3 + 6) (x + 3 - 6) = (x + 9) (x - 3)$ ，像这样，把一个二次三项式变成含有完全平方式的形式的方法，叫做配方法．

(1)、利用“配方法”因式分解： $x^{2} + 4 x y - 5 y^{2}$

(2)、如果 $a^{2} + 2 b^{2} + c^{2} - 2 a b - 6 b - 4 c + 13 = 0$ ，求 $a + b + c$ 的值．

查看试题解析
22. 如图，一轮船以40km/h的速度由西向东航行，在途中点C处接到台风警报，台风中心点B正以20km/h的速度由南向北移动．已知距台风中心200km的区域（包括边界）都属于受台风影响区．当轮船接到台风警报时，测得BC＝500km，BA＝300km．（假定轮船不改变航向）．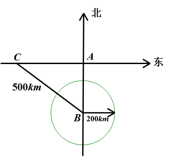

(1)、如果这艘轮船不改变航向，经过11小时，轮船与台风中心相距多远？此时，轮船是否受到台风影响？

(2)、如果这艘轮船受到台风影响，请求出轮船受到台风影响一共经历了多少小时？

查看试题解析
23. 如图1，在正方形ABCD中，点E在边AD上，连接BE交对角线AC于M，过点M作FM⊥BE交CD于F．

(1)、如图1，求证：BM＝MF；

(2)、如图2，连接BF，当AB＝6且E为AD中点时，试求CF的长．

查看试题解析