安徽省滁州市五校2022-2023学年九年级上学期期中联考数学试卷
试卷更新日期:2022-11-21 类型:期中考试
一、单选题
-
1. 若双曲线位于第一、三象限,则a的值可以是( )A、-4 B、-3 C、-2 D、-12. 甲、乙两地相距1600米,在地图上,用8厘米表示这两地的距离,那么这幅地图的比例尺是( )A、 B、 C、 D、3. 如图,两条直线被平行线 , , 所截,点A,B,C,D,E,F为截点,且 , 则的长为( )
 A、2 B、 C、 D、44. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线5. 某电子产品的售价为8000元,购买该产品时可分期付款:前期付款3000元,后期每个月分别付相同的数额,则每个月付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )A、 B、 C、 D、6. 如图,抛物线关于直线对称,点在抛物线上,那么使得的x的取值范围是( )
A、2 B、 C、 D、44. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线5. 某电子产品的售价为8000元,购买该产品时可分期付款:前期付款3000元,后期每个月分别付相同的数额,则每个月付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )A、 B、 C、 D、6. 如图,抛物线关于直线对称,点在抛物线上,那么使得的x的取值范围是( ) A、或 B、 C、 D、7. 如图,已知等边 , 点分别是边上的动点, , 则图中相似的三角形的对数是( )
A、或 B、 C、 D、7. 如图,已知等边 , 点分别是边上的动点, , 则图中相似的三角形的对数是( ) A、3对 B、4对 C、5对 D、6对8. 如图,点A在反比例函数的图象上,过点A作AB⊥x轴于点B,点C在y轴的负半轴上,若 , 则k的值为( )
A、3对 B、4对 C、5对 D、6对8. 如图,点A在反比例函数的图象上,过点A作AB⊥x轴于点B,点C在y轴的负半轴上,若 , 则k的值为( ) A、2 B、1 C、8 D、49. 如图是二次函数的图象,则函数的图象可能是( )
A、2 B、1 C、8 D、49. 如图是二次函数的图象,则函数的图象可能是( )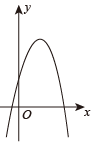 A、
A、 B、
B、 C、
C、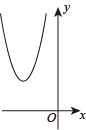 D、
D、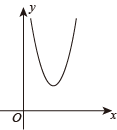 10. 如图,已知菱形的边长为2,对角线相交于点O,点M,N分别是边上的动点, , 连接 , 则下列结论错误的是( )
10. 如图,已知菱形的边长为2,对角线相交于点O,点M,N分别是边上的动点, , 连接 , 则下列结论错误的是( ) A、是等边三角形 B、的最小值是 C、当最小时, D、当时,
A、是等边三角形 B、的最小值是 C、当最小时, D、当时,二、填空题
-
11. 如果6是m与12的比例中项,那么m的值是 .12. 如图,与位似,点O为位似中心,位似比为 . 若的周长为4,则的周长是 .
 13. 如图,双曲线与正方形ABCD的边BC交于点E,与边CD交于点F,且 , , , 则 .
13. 如图,双曲线与正方形ABCD的边BC交于点E,与边CD交于点F,且 , , , 则 . 14. 如图,已知抛物线与x轴交于A,B两点,与y轴交于点C,点B的坐标为 .
14. 如图,已知抛物线与x轴交于A,B两点,与y轴交于点C,点B的坐标为 . (1)、抛物线的顶点坐标是 .(2)、已知P是抛物线对称轴l上的一个动点,当的值最小时,点P的坐标是 .
(1)、抛物线的顶点坐标是 .(2)、已知P是抛物线对称轴l上的一个动点,当的值最小时,点P的坐标是 .三、解答题
-
15. 已知 , 且 , 求值.16. 已知抛物线与x轴有交点,求m的取值范围.17. 如图,D,E分别是的边上的点, , 且 .
 (1)、求证:;(2)、求的长.18. 如图,在平面直角坐标系中,的三个顶点坐标分别为 , , .
(1)、求证:;(2)、求的长.18. 如图,在平面直角坐标系中,的三个顶点坐标分别为 , , .
⑴已知与关于y轴对称,请画出;
⑵以原点O为位似中心,在x轴上方画出的位似图形(点A,B,C的对应点分别为点 , , ),使与的位似比为 .
19. “冰墩墩”和“雪容融”两个可爱的冬奥会吉祥物以满满的“未来感”和“中国风”圈粉无数.某商家购进了A,B两种类型的冬奥会吉祥物纪念品,已知5套A型纪念品与4套B型纪念品的进货价钱一样;2套A型纪念品与1套B型纪念品的进货价共260元.(1)、求A,B两种类型纪念品每件的进货价分别是多少元?(2)、该商家准备以p元/套的售价销售A型纪念品,每天A型纪念品的销量为q套,且q与p之间的关系满足 . 如何确定售价才能使每天A型纪念品的销售利润最大?20. 如图,在矩形中,点E在边的延长线上, , 连接 , 分别交边、对角线于点F,G,. (1)、求的度数;(2)、求证: .21. 如图,直线经过点 , 交反比例函数的图象于点 .
(1)、求的度数;(2)、求证: .21. 如图,直线经过点 , 交反比例函数的图象于点 . (1)、求k的值;(2)、点D为第一象限内反比例函数图象上点B下方的一个动点,过点D作轴交线段AB于点C,连接AD,求的面积的最大值.22. 如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.
(1)、求k的值;(2)、点D为第一象限内反比例函数图象上点B下方的一个动点,过点D作轴交线段AB于点C,连接AD,求的面积的最大值.22. 如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG. (1)、填空:若∠BAF=18°,则∠DAG=°.(2)、证明:△AFC∽△AGD;(3)、若= , 请求出的值.23. 如图,抛物线(其中a,m均为常数,且 , )与x轴交于点A,B,与y轴交于点 , 顶点为F,交抛物线于点D.
(1)、填空:若∠BAF=18°,则∠DAG=°.(2)、证明:△AFC∽△AGD;(3)、若= , 请求出的值.23. 如图,抛物线(其中a,m均为常数,且 , )与x轴交于点A,B,与y轴交于点 , 顶点为F,交抛物线于点D. (1)、当a=1时,求点D的坐标;(2)、在(1)的条件下,若 , 为该抛物线上任意两点,其中 , 直接写出:当时, .(3)、若点E是第一象限内抛物线上的点,满足 , 求点E的纵坐标.
(1)、当a=1时,求点D的坐标;(2)、在(1)的条件下,若 , 为该抛物线上任意两点,其中 , 直接写出:当时, .(3)、若点E是第一象限内抛物线上的点,满足 , 求点E的纵坐标.