浙江省温州市苍南县2022-2023学年八年级上学期期中数学试卷
试卷更新日期：2022-11-21 类型：期中考试
一、选择题（本题有10小题，每小题3分，共30分.）
-
1. 下面图案是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列长度的三条线段（单位：cm），能组成三角形的是（ ）A、1，2，4 B、2，4，6 C、2，6，7 D、5，7，133. △ABC中，∠A＝40°，∠B＝80°，则∠C为（ ）A、60° B、50° C、40° D、30°4. 如图，AD是△ABC的中线，则下列结论正确的是（ ）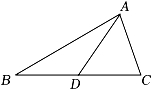
A、AB＝AC B、BD＝CD C、BD＝AD D、AC＝AD5. 在数轴上表示不等式-1≤x＜2，其中正确的是（ ）A、
B、
C、
D、
6. 如图，要测量中心湖两岸相对两点A，B的距离，可以在AB的垂线BF上取两点C，D，使CD＝BC，再在BF的垂线DG上取点E，使点A，C，E在一条直线上，可得△ABC≌△EDC.判定全等的依据是（ ）
A、SSS B、SAS C、ASA D、HL7. 下列选项中，可以用来证明命题“若a＞b，则a2＞b2”是假命题的反例是（ ）A、a＝﹣2，b＝1 B、a＝2，b＝3 C、a＝3，b＝﹣2 D、a＝2，b＝﹣38. 小李用7块长为8cm，宽为3cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AB＝BC，∠ABC＝90°），点B在DE上，点A和C分别与木墙的顶端重合，则两堵木墙之间的距离为（ ）
A、36 B、32 C、28 D、219. 如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于（ ）
A、60° B、45° C、30° D、25°10. 如图，边长为5的大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成，连结AF并延长交CD于点M.若AH＝GH，则CM的长为（ ）
A、 B、 C、1 D、二、填空题（本题有8小题，每小题3分，共24分）
-
11. 等腰三角形的顶角为80°，则底角等于.12. “x的2倍与1的差比y小”用不等式表示为.13. 如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，AC＝5，BC＝12，则CD＝.
14. 命题“同位角相等，两直线平行”的逆命题是： ．15. 如图，在△ABC中，D是AC延长线上一点，∠A＝50°，∠B＝70°，则∠BCD＝.
16. 若a＞b，且（6-x）a＜（6-x）b，则x的取值范围是.17. 如图，以直角三角形ABC的三条边为边长，向形外分别作正方形，连结CG，其中正方形ACDE和正方形ABGF的面积分别为1和5，则CG长为.
18. 如图.已知在长方形ABCD中，AB＝6，BC＝8，点E，F分别在边AD，BC上，连结BD，BE，DF.将△ABE沿BE翻折，将△DCF沿DF翻折，若翻折后，点A，C分别落在BD上的G，H处，连结CG，则四边形CGHF的周长为.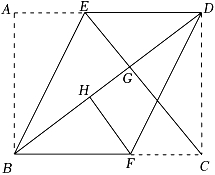
三、解答题（本题有6小题，共46分，解答需写出必要的文字说明，演算步骤或证明过程）
-
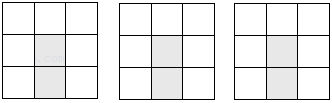
19. 在3×3的方格图中，有三个小正方形格子被涂成阴影，请在剩下的7个白色格子中选择2个格子，将它涂上阴影，使得整个图形是一个轴对称图形，要求画出三种不同形状的图形.
20. 如图，在△ABC中，AC＝BC，CD平分△ABC的外角∠ACE，试说明CD∥AB的理由.
解：∵AC＝BC（已知），
∴∠A＝∠▲ （ ）
∵CD平分∠ACE（已知）
∴∠ACD＝∠ECD（ ）
∵∠ACE＝∠A+∠B（ ）
∴∠ACE＝2∠A，∠ACE＝2∠ACD.
∴∠A＝∠▲ （等量的传递性）.
∴AB∥FE（ ）
21. 已知x＜y，请比较与的大小，并说明理由.22. 如图，点B，D，C在一条直线上，AB＝AD，AC＝AE，∠BAD＝∠CAE.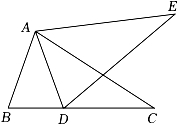
(1)、求证：BC＝DE.(2)、若∠B＝65°，求∠CDE的度数.23. 如图，在△ABC中，AB＝AC＝2 ， AD是边BC上的高线，过点D作DE∥AC交AB于点E.
(1)、求证：△ADE是等腰三角形；(2)、连结CE交AD于点H，若∠DCE＝45°，求EH的长.24. 如图，在△ABC中，∠ABC＝90°，AB＝8，BC＝AC，E是AC边上的中点，D是射线AB上的一点，连结DE，过B点作BF⊥DE于F.
(1)、求AC的长度.(2)、若点D在线段AB上.①若BD＝CE时，求证：DF＝EF.
②若△ADE是等腰三角形，求AD的长.
(3)、点A关于直线BF的对称点为A′，当A′、B、E三点共线时，求AA′＝-（请直接写出答案）.