浙江省杭州市钱江、城东片2022-2023学年七年级上学期期中数学试卷

试卷更新日期：2022-11-21 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。）

1. -5的相反数是（）

A、-5 B、5 C、±5 D、 $- \frac{1}{5}$

查看试题解析
2. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4400000000人，这个数用科学记数法表示为（　　）

A、 $44 \times 10^{8}$ B、 $4.4 \times 10^{9}$ C、 $4.4 \times 10^{8}$ D、 $4.4 \times 10^{10}$

查看试题解析
3. 下列各代数式中，符合代数式书写规则的是（）

A、 $\frac{1}{2} x^{2}$ B、 $a \times 4$ C、 $- 3 \frac{1}{3} y$ D、 $2 p \div q$

查看试题解析
4. 下列各组乘方的运算中，结果不相等的是（）

A、 $4^{2}$ 与 $2^{4}$ B、 ${(- 1)}^{2019}$ 与 $- 1^{2019}$ C、 $5^{2}$ 与 ${(- 5)}^{2}$ D、 $5^{2}$ 与 $2^{5}$

查看试题解析
5. 在下列各数中： $π$ ， $- \sqrt{3}$ ， $3.1416$ ， $\sqrt[3]{8}$ ， $\frac{22}{7}$ ，无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 下列大小关系判断正确的是（）

A、 $0 > | - 10 |$ B、 $- \frac{1}{9} > - (- \frac{1}{10})$ C、 $- 3 > - \sqrt{10}$ D、 $- 3^{2} > - π$

查看试题解析
7. 某物美超市同时卖出了两个进价不同的冰墩墩 $A$ 和 $B$ ，售价均为90元，按成本计算，超市人员发现冰墩墩 $A$ 盈利了50%，而冰墩墩 $B$ 却亏损了40%，则这次超市是（）

A、不赚不赔 B、赚了 C、赔了 D、无法判断

查看试题解析
8. 下列四个数轴上的点 $A$ 表示的数都是 $a$ ，其中一定满足为正数的是（）

A、（1） B、（2） C、（3） D、（4）

查看试题解析
9. 以下几种说法： $①$ 每一个无理数都可以用数轴上的点来表示； $②$ 近似数1.70所表示的准确数 $x$ 的范围是 $1.695 \leq x < 1.705$ ； $③$ 在数轴上表示的数在原点的左边； $④$ 立方根是它本身的数是0和1；其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图所示，圆的周长为4个单位长度，在圆的4等分点处标上字母 $A$ ， $B$ ， $C$ ， $D$ ，先将圆周上的字母 $A$ 对应的点与数轴上的数字1所对应的点重合，若将圆沿着数轴向左滚动，那么数轴上的-2022所对应的点将与圆周上字母所对应的点重合.（）

A、 $A$ B、 $B$ C、 $C$ D、 $D$

查看试题解析

二、填空题（本大题共6小题，共24.0分）

11. 若 $x = - 1$ ，则 $x^{2} - 3 x - 4 =$ .

查看试题解析
12. $\sqrt{16} =$ ， $1 - π$ 的相反数是.

查看试题解析
13. 大于-2小于 $π$ 的所有整数和是.

查看试题解析
14. 在2，5，-3，-5这四个数中任意取两个数相除，所得的商最小为.

查看试题解析
15. 有一列数按一定的规律排列为-1，3，-5，7，-9，11， $\dots \dots$ ，如果其中三个相邻的数之和为199，那么这三个相邻数中间的数为.

查看试题解析
16. 对于实数，我们规定 $[x]$ 表示不大于 $x$ 的最大整数，如 $[4] = 4 ， [\sqrt{3}] = 1 ， [- 2.5] = - 3$ ，现对82进行如下操作： $82^{第一次} [\frac{82}{\sqrt{82}}] = 9^{第二次} [\frac{9}{3}] = 3^{第三次} [\frac{3}{\sqrt{3}}] = 1$ ，这样对82只需进行3次操作后变为1，类似地，对400只需进行次操作后变为1.

查看试题解析

三、解答题（本大题共7小题，共66.0分。）

17.

(1)、已知： $- \frac{1}{2}$ 的倒数为 $a$ ， 3的相反数为 $b$ ， -1的2022次方为 $c$ ，则 $a =$ ， $b =$ ， $c =$ ；

(2)、将（1）中求出的每个数表示在数轴上.

(3)、用“ $<$ ”把 $a$ ， $b$ ， $c$ 连接起来.

查看试题解析
18. 请根据下面的文字语言，写出相应的代数式或者举出一个符合文字语言的式子来说明.

(1)、x的3倍除以 $y$ 的4倍所得的商：；（代数式）

(2)、m与 $n$ 的差的平方根：；（代数式）

(3)、两个无理数的和为有理数：；（符合文字语言的式子）

(4)、三数相加，和小于其中两个加数，大于第三个加数：.（符合文字语言的式子）

查看试题解析
19. 计算：

(1)、 $(+ \frac{3}{5}) - (- \frac{1}{2}) + (- \frac{3}{5}) + (+ 9.5)$ ；

(2)、 $(\frac{7}{9} - \frac{5}{6} + \frac{7}{12}) \times (- 36)$ ；

(3)、 $\sqrt{0.25} - \sqrt{13^{2} - 12^{2}}$ ；

(4)、 $- 1^{2} + 36 \div {(- 3)}^{2} - (- 3 \frac{3}{7}) \times (- \frac{7}{24}) .$

查看试题解析
20. 已知 $| a | = 5$ ， $b^{2} = 4$ ， $c^{3} = - 8$ .

(1)、若 $a < b$ ，求 $a + b$ 的值；

(2)、若 $a b c > 0$ ，求 $a - 3 b - 2 c$ 的值.

查看试题解析
21. 观察下边图形，每个小正方形的边长为1.

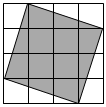(1)、则图中阴影部分的面积是，边长是.

(2)、已知阴影正方形的边长为 $x$ ，且 $a < x < b$ ，若 $a$ 和 $b$ 是相邻的两个整数，那么 $a =$ ， $b =$ .

(3)、若设如图阴影正方形的边长为 $x$ ，请在下面的数轴上准确地作出数 $x$ 所表示的点，若还有一个点 $B$ 与它的距离为1，则这个点 $B$ 在数轴上所表示的数为.

查看试题解析

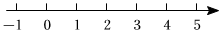22. 有20箱苹果，以每箱15千克为标准，超过15千克的数记为正数，不足15千克的数记为负数，称重记录如下：

与标准质量的差 $($ 千克 $)$	-0.5	-0.4	-0.2	0	+0.2	+0.3	+0.6
箱数 $($ 箱 $)$	2	1	5	2	4	2	4

(1)、最重的一箱比最轻的一箱重千克；

(2)、求这20箱苹果的总质量；

(3)、若这批苹果的批发价是8.5元

/

千克，售价是15元

/

千克，运输和出售过程中有10%的苹果腐烂无法出售，则出售这20箱苹果能盈利多少元？

查看试题解析

23. 阅读理解：
某节数学课上，杜老师在复习数轴上的点与数之间的关系时，给出了以下定义：

若 $A$ ， $B$ ， $C$ 是数轴上的三个点，如果点 $C$ 到 $A$ 的距离等于点 $C$ 到 $B$ 的距离，那么我们就称点 $C$ 是点 $A$ ， $B$ 的中点.

例如，如图1，点 $A$ 表示的数为-1，点 $B$ 表示的数为3，表示数1的点 $C$ 到点 $A$ 的距离是 $2$ ，到点 $B$ 的距离是2，那么点 $C$ 是点 $A$ ， $B$ 的中点.

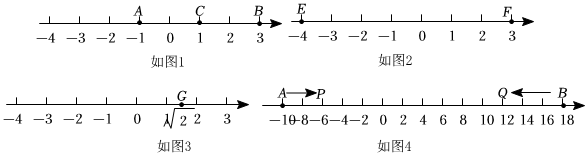
【知识运用】

(1)、如图2， $E$ 、 $F$ 为数轴上两点，点 $E$ 所表示的数为-4，点 $F$ 所表示的数为3数所表示的点是点 $E$ ， $F$ 的中点.

(2)、①如图3，若数 $\sqrt{2}$ 所表示的点 $G$ 是点 $M$ ， $N$ 的中点，其中点 $M$ ， $N$ 所表示的数分别为 $m$ ， $n .$ 那么 $m =$ ， $n =$ $. ($ 只要写出符合条件的一对值即可 $)$ .
$②$ 若数 $g$ 所表示的点 $G$ 是点 $M$ ， $N$ 的中点，其中点 $M$ ， $N$ 所表示的数分别为 $m$ ， $n .$ 那么 $g =$ $. ($ 用 $m$ ， $n$ 的代数式表示 $)$

(3)、如图4， $A$ ， $B$ 为数轴上两点，点 $A$ 所表示的数为-10，点 $B$ 所表示的数为18，现有一只电子蜗牛 $P$ 从点 $A$ 出发，1个单位每秒的速度向右运动；同时另一只电子蜗牛 $Q$ 从点 $B$ 出发，以2个单位每秒的速度向左运动，若点 $M$ ， $N$ 分别是 $A P$ 和 $B Q$ 的中点，则在 $P$ ， $Q$ 的运动过程中，当 $t =$ 秒时，点 $M$ ， $N$ 到原点的距离相等 $($ 请直接写出答案 $)$ .

查看试题解析