浙江省宁波七中教育集团2022-2023学年九年级上学期数学学习效果自我评估试题卷

试卷更新日期：2022-11-21 类型：期中考试

进入出卷网下载

一、选择题（每小题4分，共40分）

1. 下列事件中，属于不可能事件的是（）

A、x是实数，则 $x^{2} \geq 0$ B、人在月球上所受的重力比在地球上小 C、任意选择某电视频道，正在播放动画片 D、一个三角形三个内角的和小于180°

查看试题解析
2. 若 $\frac{b}{a} = \frac{3}{7}$ ，则 $\frac{b + a}{a - b}$ 的值等于（）

A、 $\frac{1}{2}$ B、 $\frac{5}{2}$ C、 $\frac{5}{3}$ D、 $\frac{5}{4}$

查看试题解析
3. 将抛物线 $y = \frac{1}{2} x^{2} - 6 x + 21$ 向左平移2个单位后，得到新抛物线的解析式为（）

A、 $y = \frac{1}{2} {(x - 8)}^{2} + 5$ B、 $y = \frac{1}{2} {(x - 4)}^{2} + 5$ C、 $y = \frac{1}{2} {(x - 4)}^{2} + 3$ D、 $y = \frac{1}{2} {(x - 8)}^{2} + 3$

查看试题解析
4. 如图，是二次函数y=ax²+bx+c的部分图象，由图象可知不等式ax²+bx+c<0的解集是（）

A、 $- 1 < x < 5$ B、 $x > 5$ C、 $x < - 1 且 x > 5$ D、 $x < - 1 或 x > 5$

查看试题解析
5. 如图，D是等边△ABC外接圆上的点，且∠DAC＝20°，则∠ACD的度数为（）

A、40° B、45° C、20° D、30°

查看试题解析
6. 如图，在△ABC中，AC=2，BC=4，D为BC边上的一点，且∠CAD=∠B．若△ADC的面积为 $a$ ，则△ABD的面积为（）

A、 $2 a$ B、 $\frac{5}{2} a$ C、 $3 a$ D、 $\frac{7}{2} a$

查看试题解析
7. 如图1，是装了液体的高脚杯示意图（数据如图）用去一部分液体后如图2所示，此时液面直径AB＝（）

A、2cm B、2.5cm C、3cm D、4cm

查看试题解析
8. 小明给出如下题目：二次函数y=ax²+bx+c（a≠0）的图象如图所示，点A坐标为 $(- 1 ， 0)$ ，给出下列结论：
① b²-4ac＞0；② b+2a＜0；③ 当x＞3时，y＜0；④ 3a+b＞0；⑤ $a ： b ： c = - 1 ： 2 ： 3$
其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
9. 如图，G是△ABC的重心，延长BG交AC于点D，延长CG交AB于点E，P，Q分别是△BCE和△BCD的重心，BC长为12，则PQ的长为（）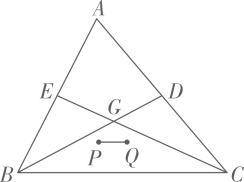

A、2 B、2.5 C、3 D、4

查看试题解析
10. 如图，“心”形是由抛物线 $y = - x^{2} + 6$ 和它绕着原点O，顺时针旋转60°的图形经过取舍而成的，其中顶点C的对应点为D，点A，B是两条抛物线的两个交点，直线AB为“心”形对称轴，点E，F，G 是抛物线与坐标轴的交点，则AB=（）

A、 $6 \sqrt{3}$ B、8 C、10 D、 $10 \sqrt{3}$

查看试题解析

二、填空题（每小题5分，共30分）

11. 若一个正多边形的每个内角为150°，则这个正多边形的边数是．

查看试题解析
12. 在－2，－1，0，1，2这五个数中任取两数m，n，则二次函数 $y = {(x - m)}^{2} + n$ 的顶点在坐标轴上的概率为．

查看试题解析
13. 如图，把一个长方形划分成三个全等的小长方形，若要使每一个小长方形与原长方形相似，则原长方形应满足 $AD ： CD$ = ．

查看试题解析
14. 如图，有一块直角三角形余料ABC，∠BAC＝90°，现从中切出一条矩形纸条DEFG，其中E，F在BC上，点G在AB上，点D在AC上，若BF＝4.5cm，CE＝2cm，则纸条GF长为cm．

查看试题解析
15. 如图，⊙O中，弦AC= $\sqrt{15}$ ，沿AC折叠劣弧 $\overset{⌢}{A C}$ 交直径AB于D，DB= $\frac{1}{2}$ ，则直径AB= ．

查看试题解析
16. 如图，线段BC的长为 8，以B为圆心，4为半径作⊙B，点A是⊙B上一动点，连接AC，将线段AC绕点A逆时针旋转90°得到线段AD，连接DB，则DB的最小值为．

查看试题解析

三、解答题（本大题有8小题，第17～20小题每小题8分，第21小题10分，第22、23小题每小题12分，第24小题14分，共80分）

17. 一只不透明的袋子中装4个球，其中3个白球和1个黑球，它们除颜色外都相同．

(1)、求摸出一个球是白球的概率．

(2)、摸出一个球，记下颜色后不放回，再摸出1个球，求两次摸到的球颜色相同的概率（要求画树状图或列表）．

查看试题解析
18. 如图，已知AD∥BE∥CF，它们依次交直线l₁ ， l₂ ，于点A，B，C和点D，E，F.

(1)、如果AB＝6，BC＝8，DF＝7，求EF的长．

(2)、如果AB：AC＝2：5，EF＝9，线段x是线段DE和线段DF的比例中项，求x的值．

查看试题解析
19. 已知二次函数图象的顶点是 $(- 1 ， 2)$ ，且过点 $（ 0 ， \frac{3}{2} ）$ ．

(1)、求二次函数的表达式．

(2)、求当 $- 2 < x < 4$ 时，函数的最大值和最小值．

(3)、求当x取何值时， $y > 0$

查看试题解析
20. 如图，由小正方形构成的6×6网格，每个小正方形的顶点叫做格点．⊙O经过A，B，C三个格点，仅用无刻度的直尺在给定网格中按要求画图．（保留作图痕迹）

(1)、在图①中的圆上找一点D（不与点B重合），使∠ADC＝90°；

(2)、在图②中的圆上找一点E，使OE平分弧AB；

(3)、在图③中的圆上找一点F，使AF平分∠BAC．

查看试题解析
21. 如图，AB是⊙O的直径，点C为 $\overset{⌢}{B D}$ 的中点，CF为⊙O的弦，且CF⊥AB，垂足为点E，连结BD交CF于点G，连结CD，AD，BF．

(1)、求证：△BFG≌△CDG；

(2)、若AD=10，EF=15，求BE的长．

查看试题解析
22. 某电商平台，在国庆长假期间，举行了商品打折促销活动，经市场调查发现，某种商品的周销量y（件）是关于售价x（元/件）的一次函数，下表仅给出了该商品售价x、周销售量y，周销售利润w（元）的三组对应值数据：

x

40

70

90

y

180

90

30

w

3600

4500

2100

注：周销售利润=周销量×（售价—进价）

(1)、求y关于x的函数表达式（不要求写出自变量的取值范围）．

(2)、若该商品的进价为a元/件，则当售价为多少时，周销售利润最大？并求出此时的最大利润．

(3)、因疫情原因，该商品进价提高了m元/件（m>0），公司为回馈消费者，规定该商品的售价不得超过55元/件，且该商品在今后的销售中，周销售与售价仍然满足（1）中的函数关系，若周销售利润最大为4050元，求m的值．

查看试题解析
23. 如图1，折叠矩形纸片ABCD，具体操作：①点E为AD边上一点（不与点A、D重合），把△ABE沿BE所在的直线折叠，A点的对称点为F点；②过点E对折∠DEF，折痕EG所在的直线交DC于点G、D点的对称点为H点．

(1)、求证：△ABE∽△DEG．

(2)、若AB=6，BC=10，
①点E在移动的过程中，求DG的最大值；

②如图2，若点C恰在直线EF上，连接DH，求△DGH的面积．

查看试题解析
24. 定义：△ABC中， $∠ A + \frac{1}{2} ∠ B = 90^{0}$ ，则称△ABC为半余三角形，∠B叫做半余角．

(1)、如图1，⊙O中，BC是直径，求证：△AOC为半余三角形．

(2)、下列说法正确的是．
①半余三角形一定是钝角三角形；

②直角三角形不可能是半余三角形；

③任何直角三角形都能分割成两个半余三角形．

(3)、如图2，⊙O中，BC是直径，AB=6，AC=8，点D是线段AC上一点（不与点A、点C重合），若△AOD为半余三角形，求OD的长．

(4)、如图3，点E是直径BC上一点，△ABE为半余三角形，且∠BAE为半余角，过点E作EF⊥BC交AC于点F，若△ABC的面积为△AEF面积的7.5倍，求 $\frac{A E}{B C}$ 的值．

查看试题解析

x	40	70	90
y	180	90	30
w	3600	4500	2100