2023年春季浙教版数学九年级下册第三章《投影与三视图》单元检测B

试卷更新日期：2022-11-20 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图是一物体的三视图，则这个几何体的侧面积为（）

A、 $200 π$ B、 $100 π$ C、 $100 \sqrt{3} π$ D、 $500 π$

查看试题解析
2. 某商场的休息椅如图所示，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 在一仓库里堆放着若干个大小相同的正方体小货箱，仓库管理员将从三个方向看到的物体的形状图画了出来，如图所示，则这堆正方体小货箱共有（）

A、11个 B、10个 C、9个 D、8个

查看试题解析
4. 下列图形中经过折叠，可以围成圆锥的是（）

A、 B、 C、 D、

查看试题解析
5. 一个正方体的相对的表面上所标的数都是互为相反数的两个数，如图是这个正方体的表面展开图，那么图中x的值是（）

A、－8 B、－3 C、－2 D、3

查看试题解析
6. 如图，电灯 $P$ 在横杆 $A B$ 的正上方， $A B$ 在灯光下的影长为 $C D$ ， $A B / / C D$ ， $A B = 2 m$ ， $C D = 5 m$ ，点 $P$ 到 $C D$ 的距离是 $3 m$ ，则点 $P$ 到 $A B$ 的距离是（）

A、 $\frac{5}{6} m$ B、 $\frac{6}{7} m$ C、 $\frac{6}{5} m$ D、 $\frac{10}{3} m$

查看试题解析
7. 如图所示是滨河公园中的两个物体一天中四个不同时刻在太阳光的照射下落在地面上的影子，按照时间的先后顺序排列正确的是（）

A、(3)(4)(1)(2) B、(4)(3)(1)(2) C、(4)(3)(2)(1) D、(2)(4)(3)(1)

查看试题解析
8. 如图是一根空心方管，在研究物体的三种视图时，小明画出的该空心方管的主视图与俯视图分别是（）

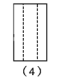A、（1）（3） B、（1）（4） C、（2）（3） D、（2）（4）

查看试题解析
9. 下图所示的长方形（长为14，宽为8）硬纸板，剪掉阴影部分后，将剩余的部分沿虚线折叠，制作成底面为正方形的长方体箱子，则长方体箱子的体积为（）

A、56 B、40 C、28 D、20

查看试题解析
10. 如图（1）是一个小正方体的表面展开图，小正方体从图（2）所示位置依次翻转到第①格、第②格，第③格，第④格，这时小正方体朝上一面的字是（）

A、六 B、中 C、学 D、强

查看试题解析

二、填空题（每题3分，共18分）

11. 如图，已知路灯离地面的高度AB为4.8m，身高为1.6 m的小明站在D处的影长DC为2 m，那么此时小明离路灯杆AB的距离BD为m

查看试题解析
12. 三棱柱的三视图如图所示，在俯视图△EFG中，FG=18cm，EG=14cm，∠EGF=30°，则左视图中AB的长为cm．

查看试题解析
13. 一个几何体由若干大小相同的小正方体搭成，如图分别是从它的正面、上面看到的形状图，若组成这个几何体的小正方体最少需要m个，最多需要n个，则m﹣n＝．

查看试题解析
14. 在同一时刻两根木竿在太阳光下的影子如图所示，其中木竿AB＝2m，它的影子BC＝1.5m，木竿PQ的影子有一部分落在了墙上，它的影子QN＝1.8m，MN＝0.8m，木竿PQ的长度为．

查看试题解析
15. 图2是图1中长方体的三视图，用S表示面积，S_主＝x²+2x，S_左＝x²+x，则S_俯＝．

查看试题解析
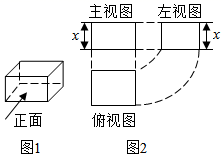16. 已知某几何体的三视图如图所示，则该几何体的体积为．

查看试题解析

三、解答题（共8题，共72分）

17. 在数学实验课上，小莹将含 $30 °$ 角的直角三角尺分别以两个直角边为轴旋转一周，得到甲、乙两个圆锥，并用作图软件Geogebra画出如下示意图
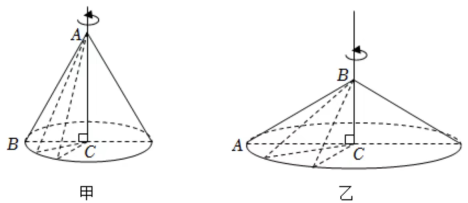
小亮观察后说：“甲、乙圆锥的侧面都是由三角尺的斜边 $A B$ 旋转得到，所以它们的侧面积相等．”
你认同小亮的说法吗？请说明理由．

查看试题解析
18. 如图，是一个几何体的表面展开图．

(1)、该几何体是．

(2)、依据图中数据求该几何体的表面积和体积．

查看试题解析
19. 如图，由六个棱长为1cm的小正方体组成一个几何体．

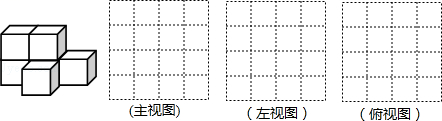(1)、分别画出这个几何体的主视图、左视图、俯视图．

(2)、该几何体的表面积是cm² ．

查看试题解析
20. 一块材料的形状是等腰△ABC，底边 BC=120 cm，高 AD=120 cm.

(1)、若把这块材料加工成正方形零件，使正方形的一边在 BC 上，其余两个顶点分别在AB，AC 上（如图 1），则这个正方形的边长为多少？

(2)、若把这块材料加工成正方体零件（如图 2，阴影部分为正方体展开图），则正方体的表面积为多少？

查看试题解析
21. 一个正方体的六个面分别标有字母A、B、C、D、E、F，从三个不同方向看到的情形如图所示．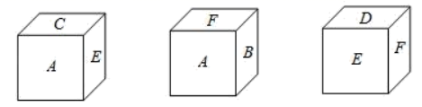

(1)、A的对面是， B的对面是， C的对面是；（直接用字母表示）

(2)、若 $A = - 2$ ， $B = | m - 3 |$ ， $C = - (m - n)$ ， $E = {(2 + n)}^{2}$ ，且小正方体各对面上的两个数都互为相反数，请求出F所表示的数．

查看试题解析

22. 为了测量学校旗杆（垂直于水平地面）的高度，班里三个兴趣小组设计了三种不同的测量方案，如下表所示.

课题	测量校园旗杆的高度
测量工具	测角仪（测量角度的仪器），卷尺，平面镜等
测量小组	A组	B组	C组
测量方案示意图
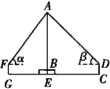
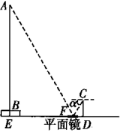
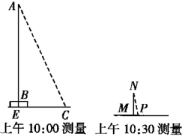
说明	线段AB表示旗杆的高度，线段BE表示旗杆底座高度，点A，B，E共线，线段CD，FG表示测角仪的高度，点A，B，C，D，E，F，G在同一竖直平面内，CG表示两次测角仪摆放位置的距离，测角仪可测得旗杆顶端A的仰角	线段AB表示旗杆的高度，线段BE表示旗杆底座高度，点A，B，E共线，线段CD表示测角仪的高度，DE表示测角仪到旗杆的距离，点F表示平面镜的中心，点E，F，D共线，眼睛在C处，移动平面镜，看向中心F，恰好看到旗杆顶端A，此时用测角仪测得平面镜的俯角，A，B，C，D，E，F六点在同一竖直平面内	线段AB表示旗杆的高度，线段BE表示旗杆底座高度，点A，B，E共线，EC为旗杆与底座某一时刻下的影长，A，B，C，E四点在同一竖直平面内，标杆NM垂直于水平地面，PM为标杆NM在某一时刻的影长
测量数据	$α$ 为 $53 °$ ， $β$ 为 $45 °$ ， $C D = F G = 1.5$ 米， $B E = 0.5$ 米， $C G = 14.79$ 米	$D E = 6.61$ 米， $C D = 1.5$ 米， $B E = 0.5$ 米， $α$ 为 $60 °$	$C E = 4.66$ 米， $M N = 1$ 米， $M P = 0.21$ 米， $B E = 0.5$ 米