2023年春季浙教版数学九年级下册第二章 《直线与圆的位置关系》单元检测B
试卷更新日期:2022-11-20 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 如图,AB是 的切线, B 为切点,连接AO交 于点C,延长AO交 于点 D,连接BD.若 ,且 ,则AB的长度是( )
 A、3 B、4 C、 D、2. 如图, 与正五边形 的两边 相切于 两点,则 的度数是( )
A、3 B、4 C、 D、2. 如图, 与正五边形 的两边 相切于 两点,则 的度数是( )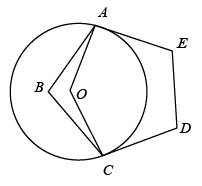 A、 B、 C、 D、3. 如图,是的直径,点 , 在上,点是的中点,过点画的切线,交的延长线于点 , 连接 . 若 , 则的度数为( )
A、 B、 C、 D、3. 如图,是的直径,点 , 在上,点是的中点,过点画的切线,交的延长线于点 , 连接 . 若 , 则的度数为( ) A、 B、 C、 D、4. 如图,在四边形材料中, , , , , .现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
A、 B、 C、 D、4. 如图,在四边形材料中, , , , , .现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )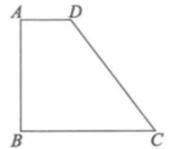 A、 B、8cm C、 D、10cm5. 如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是( )
A、 B、8cm C、 D、10cm5. 如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是( )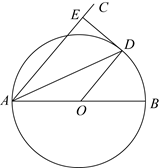 A、AE⊥DE B、AE//OD C、DE=OD D、∠BOD=50°6. 如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接 , , , 当 , , 时,的长为( )
A、AE⊥DE B、AE//OD C、DE=OD D、∠BOD=50°6. 如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接 , , , 当 , , 时,的长为( )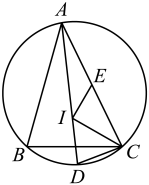 A、5 B、4.5 C、4 D、3.57. 如图,直角坐标系中,以5为半径的动圆的圆心A沿x轴移动,当⊙ 与直线 只有一个公共点时,点A的坐标为( )
A、5 B、4.5 C、4 D、3.57. 如图,直角坐标系中,以5为半径的动圆的圆心A沿x轴移动,当⊙ 与直线 只有一个公共点时,点A的坐标为( ) A、 B、 C、 D、8. 如图,在 中, , ,点 在 上, ,以 为半径的 与 相切于点 ,交 于点 ,则 的长为( )
A、 B、 C、 D、8. 如图,在 中, , ,点 在 上, ,以 为半径的 与 相切于点 ,交 于点 ,则 的长为( )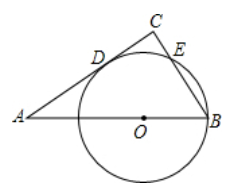 A、 B、 C、 D、19. 如图,在边长为2的正方形 中, 是以 为直径的半圆的切线,则图中阴影部分的面积为( )
A、 B、 C、 D、19. 如图,在边长为2的正方形 中, 是以 为直径的半圆的切线,则图中阴影部分的面积为( )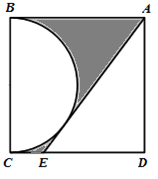 A、 B、 C、1 D、10. 如图,在△ABC中,AB=6,以点A为圆心,3为半径的圆与边BC相切于点D , 与AC , AB分别交于点E和点G , 点F是优弧GE上一点,∠CDE=18°,则∠GFE的度数是( )
A、 B、 C、1 D、10. 如图,在△ABC中,AB=6,以点A为圆心,3为半径的圆与边BC相切于点D , 与AC , AB分别交于点E和点G , 点F是优弧GE上一点,∠CDE=18°,则∠GFE的度数是( )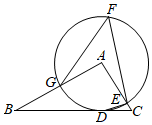 A、50° B、48° C、45° D、36°
A、50° B、48° C、45° D、36°二、填空题(每题3分,共18分)
-
11. 如图,AB与⊙O相切于点C,AO=3,⊙O的半径为2,则AC的长为.
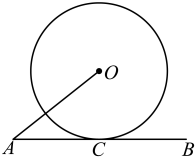 12. 如图,木工用角尺的短边紧靠⊙О于点A,长边与⊙О相切于点B,角尺的直角顶点为C,已知AC=6cm,CB=8cm,则⊙О的半径为cm.
12. 如图,木工用角尺的短边紧靠⊙О于点A,长边与⊙О相切于点B,角尺的直角顶点为C,已知AC=6cm,CB=8cm,则⊙О的半径为cm.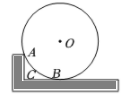 13. 如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .
13. 如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .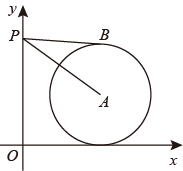 14. 我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为.
14. 我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为. 15. 如图,已知AB是⊙O的弦,∠AOB=120°,OC⊥AB,垂足为C,OC的延长线交⊙O于点D.若∠APD是 所对的圆周角,则∠APD的度数是
15. 如图,已知AB是⊙O的弦,∠AOB=120°,OC⊥AB,垂足为C,OC的延长线交⊙O于点D.若∠APD是 所对的圆周角,则∠APD的度数是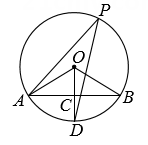 16. 如图,等边三角形ABC的边长为4, 的半径为 ,P为AB边上一动点,过点P作 的切线PQ,切点为Q,则PQ的最小值为.
16. 如图,等边三角形ABC的边长为4, 的半径为 ,P为AB边上一动点,过点P作 的切线PQ,切点为Q,则PQ的最小值为.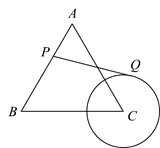
三、解答题(共8题,共72分)
-
17. 如图,AB是⊙O的直径,E为⊙O上的一点,∠ABE的平分线交⊙O于点C,过点C的直线交BA的延长线于点P,交BE的延长线于点D.且∠PCA=∠CBD.
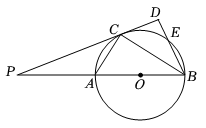 (1)、求证:PC为⊙O的切线;(2)、若PC=BO,PB=12,求⊙O的半径及BE的长.18. 如图,在 中, .以AB为直径的 与线段BC交于点D,过点D作 ,垂足为E,ED的延长线与AB的延长线交于点P.
(1)、求证:PC为⊙O的切线;(2)、若PC=BO,PB=12,求⊙O的半径及BE的长.18. 如图,在 中, .以AB为直径的 与线段BC交于点D,过点D作 ,垂足为E,ED的延长线与AB的延长线交于点P. (1)、求证:直线PE是 的切线;(2)、若 的半径为6, ,求CE的长.19. 如图,在半径为10cm的⊙O中,AB是⊙O的直径,CD是过⊙O上一点C的直线,且AD⊥DC于点D,AC平分∠BAD,点E是BC的中点,OE=6cm.
(1)、求证:直线PE是 的切线;(2)、若 的半径为6, ,求CE的长.19. 如图,在半径为10cm的⊙O中,AB是⊙O的直径,CD是过⊙O上一点C的直线,且AD⊥DC于点D,AC平分∠BAD,点E是BC的中点,OE=6cm. (1)、求证:CD是⊙O的切线;(2)、求AD的长.20. 如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD.
(1)、求证:CD是⊙O的切线;(2)、求AD的长.20. 如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD. (1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.21. 如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G交AC于点H.
(1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.21. 如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G交AC于点H. (1)、求证:CD是⊙O的切线;(2)、延长AB和DC交于点E,若AE=4BE,求cos∠DAB的值;(3)、在(2)的条件下,求的值.22. 如图,已知 , 是的直径,是的切线,点在的延长线上, , 交于点 ,
(1)、求证:CD是⊙O的切线;(2)、延长AB和DC交于点E,若AE=4BE,求cos∠DAB的值;(3)、在(2)的条件下,求的值.22. 如图,已知 , 是的直径,是的切线,点在的延长线上, , 交于点 , (1)、求证:;(2)、求证:;(3)、若的面积 , 求四边形的面积.23. 如图,已知D为⊙O上一点,点C在直径BA的延长线上,BE与⊙O相切,交CD的延长线于点E,且.
(1)、求证:;(2)、求证:;(3)、若的面积 , 求四边形的面积.23. 如图,已知D为⊙O上一点,点C在直径BA的延长线上,BE与⊙O相切,交CD的延长线于点E,且. (1)、判断CD与⊙O的位置关系,并说明理由;(2)、若 , ,
(1)、判断CD与⊙O的位置关系,并说明理由;(2)、若 , ,①求⊙O的半径;
②求BD的长.
24. 如图,以AB为直径的⊙O与AH相切于点A,点C在AB左侧圆弧上,弦CD⊥AB交⊙O于点D,连结AC,AD,点A关于CD的对称点为E,直线CE交⊙O于点F,交AH于点G, (1)、求证:∠CAG=∠AGC:(2)、当点E在AB上,连结AF交CD于点卫,若 ,求 的值;(3)、当点E在射线AB上,AB=2,以点A,C,O,F为顶点的四边形中有一组对边平行时,求AE的长.
(1)、求证:∠CAG=∠AGC:(2)、当点E在AB上,连结AF交CD于点卫,若 ,求 的值;(3)、当点E在射线AB上,AB=2,以点A,C,O,F为顶点的四边形中有一组对边平行时,求AE的长.