浙教版备考2023年中考数学一轮复习2.绝对值
试卷更新日期:2022-11-20 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 有理数-2, ,0, 中,绝对值最大的数是( )A、-2 B、 C、0 D、2. 计算的最后结果是( )A、3 B、-3 C、-5 D、53. 下列说法正确的是( )A、0既不是整数,也不是分数. B、一个数的绝对值一定是正数. C、一个有理数不是整数,就是分数 D、绝对值等于它本身的数是0和14. 已知 , b是的相反数,则a+b的值为( )A、或 B、 C、 D、或5. 若 , 则的值为( )A、-4 B、-1 C、0 D、46. 下列说法正确的是( )A、若 ,则 B、a为任何有理数,则必为负数 C、两个有理数的和为负数,则这两个数中至少有一个是负数 D、若 , 则a为非负数7. 下列各式中,结果一定为正数的是( )A、a2+b2 B、|a|﹣|b| C、|a|+b D、|a|8. 数轴上三点所代表的数分别是且 . 下列选项中,表示三点在数轴上的位置关系正确的是( )A、
 B、
B、 C、
C、 D、
D、 9. 已知a,b是有理数, , ,若将a,b在数轴上表示,则图中有可能( )A、
9. 已知a,b是有理数, , ,若将a,b在数轴上表示,则图中有可能( )A、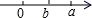 B、
B、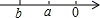 C、
C、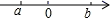 D、
D、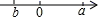 10. |x-2|+|x-4|+|x-6|+|x-8|的最小值是a, , 那么的值为( )A、0 B、-1 C、-2 D、不确定
10. |x-2|+|x-4|+|x-6|+|x-8|的最小值是a, , 那么的值为( )A、0 B、-1 C、-2 D、不确定二、填空题(每空2分,共18分)
-
11. 已知 , , 且 , 求 .12. 绝对值小于2021的所有的整数的和是 .13. 如果x、y都是不为0的有理数,则代数式的最小值是 .14. 根据数轴化简:|a|= , |-b|= , |a-b|=
 15. 算式10﹣|5﹣x|有最(填“大”或“小”)值为 .16. p、q、r、s在数轴上的位置如图所示:若|p-r|=10,|p-s|=12,|q-s|=9, 则|q-r|的值为.
15. 算式10﹣|5﹣x|有最(填“大”或“小”)值为 .16. p、q、r、s在数轴上的位置如图所示:若|p-r|=10,|p-s|=12,|q-s|=9, 则|q-r|的值为.
三、解答题(共9题,共72分)
-
17. 计算(1)、( - 9)- ( - 7) + ( - 6)- |4| - ( - 5)(2)、-( - 2)- + 1 - +( - )(3)、(4)、(5)、(6)、18. 已知 与|x-y-3|互为相反数,求 的值.19. 先化简,再求值: , 其中a,b满足 .20. 在数轴上表示下列各数及它们的相反数,并用“<”把这些数连接起来.-(+2),0,-|-1.2|,+ .21.(1)、已知有理数 , , 且ab<0,求a﹣b的值.(2)、已知有理数a,b,c满足 , 求a+b﹣c的值.22. 学们,我们都知道:|5-2|表示5与2的差的绝对值,实际上也可理解为5与2两数在数轴上所对应的两点之间的距离;|5+2|表示5与-2的差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,试探索:(1)、|-4+6|=;|-2-4|=;(2)、找出所有符合条件的整数x,使|x+2|+|x-1|=3成立;(3)、若数轴上表示数a的点位于-4与6之间,求|a+4|+|a-6|的值;
(4)、当a=时,|a-1|+|a+5|+|a-4|的值最小,最小值是;23. 对于含绝对值的算式,在有些情况下,可以不需要计算出结果也能将绝对值符号去掉,例如:|7-6|=7-6;|6-7|=7-6;; .观察上述式子的特征,解答下列问题:
(1)、把下列各式写成去掉绝对值符号的形式(不用写出计算结果):①|23-47|=;②=;
(2)、当a>b时,|a-b|=;当a<b时,|a-b|=;(3)、计算: .24. 在解决数学问题的过程中,我们常用到"分类讨论"的数学思想,下面是运用"分类讨论"的数学思想解决问题的过程,请仔细阅读,并解答问题.(提出问题)已知有理数a,b,c满足abc>0,求 的值.
(解决问题)解∶由题意,得 a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都为正数,即a>0,b>0,c>0时, = =1+1+1=3
②当a,b,c中有一个为正数,另两个为负数时,不妨设a>0,b<0,c<0,则 = =1+(-1)+(-1)=-1
综上所述, 的值为3或-1
(探究拓展)
请根据上面的解题思路解答下面的问题:
(1)、已知a,b是不为0的有理数,当|ab|=-ab时, =(2)、已知a,b,c是有理数,当abc<0时,求 + =(3)、已知a,b,c是有理数,a+b+c=0,abc<0,求 =25. 根据 ,我们可以化简含有绝对值的代数式,如化简代数式 时,可令 ,得到零点值 ,则 .类似地,我们可以化简 :当 时,原式 ;
当 时,原式 ;
当 时,原式 ,
综上所述,原式 ;
(1)、化简 时,先确定零点值分别为 和 .(2)、仿照上面的做法,化简 .(3)、仿照上面的做法,化简 .