2023年春季浙教版数学九年级下册第二章 《直线与圆的位置关系》单元检测A
试卷更新日期:2022-11-20 类型:单元试卷
一、单选题(每题3分,共30分)
-
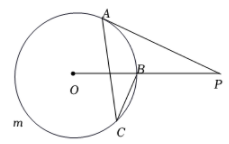
1. 如图,PA,PB是的切线,A、B为切点,若 , 则的度数为( )
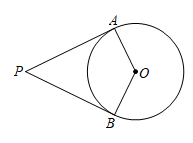 A、 B、 C、 D、2. 如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为( )
A、 B、 C、 D、2. 如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为( ) A、 B、 C、 D、3. 为⊙ 外一点, 与⊙ 相切于点 , , ,则 的长为( )A、 B、5 C、8 D、94. 如图,AB是⊙O的直径,C为 ⊙O上一点,过点 C的切线与 AB 的延长线交于点 P,若 AC=PC= ,则 PB 的长为( )
A、 B、 C、 D、3. 为⊙ 外一点, 与⊙ 相切于点 , , ,则 的长为( )A、 B、5 C、8 D、94. 如图,AB是⊙O的直径,C为 ⊙O上一点,过点 C的切线与 AB 的延长线交于点 P,若 AC=PC= ,则 PB 的长为( )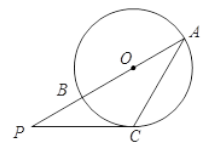 A、 B、 C、 D、35. 如图,PA,PB是⊙O的切线,A,B是切点,若 ,则 ( )
A、 B、 C、 D、35. 如图,PA,PB是⊙O的切线,A,B是切点,若 ,则 ( ) A、 B、 C、 D、6. 如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )
A、 B、 C、 D、6. 如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )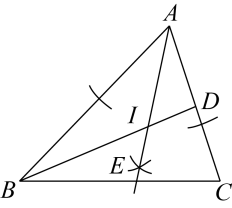 A、I到AB,AC边的距离相等 B、CI平分∠ACB C、I是△ABC的内心 D、I到A,B,C三点的距离相等7. 如图,等边内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边的内心成中心对称,则圆中的黑色部分的面积与的面积之比是( )
A、I到AB,AC边的距离相等 B、CI平分∠ACB C、I是△ABC的内心 D、I到A,B,C三点的距离相等7. 如图,等边内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边的内心成中心对称,则圆中的黑色部分的面积与的面积之比是( ) A、 B、 C、 D、8. 如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接 , , , 当 , , 时,的长为( )
A、 B、 C、 D、8. 如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接 , , , 当 , , 时,的长为( )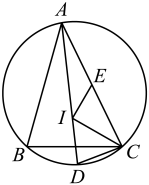 A、5 B、4.5 C、4 D、3.59. 如图所示,已知三角形为直角三角形,为圆切线,为切点,则和面积之比为( )
A、5 B、4.5 C、4 D、3.59. 如图所示,已知三角形为直角三角形,为圆切线,为切点,则和面积之比为( )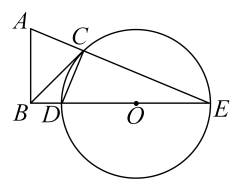 A、 B、 C、 D、10. 如图,是的直径,点P在的延长线上,与相切于点A,连接 , 若 , 则的度数为( )
A、 B、 C、 D、10. 如图,是的直径,点P在的延长线上,与相切于点A,连接 , 若 , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,PA与⊙O相切于点A,PO与⊙O相交于点B,点C在 上,且与点A,B 不重合,若∠P=26°,则∠C的度数为°.
 12. 如图,在中, , 半径为3cm的是的内切圆,连接、 , 则图中阴影部分的面积是cm2.(结果用含的式子表示)
12. 如图,在中, , 半径为3cm的是的内切圆,连接、 , 则图中阴影部分的面积是cm2.(结果用含的式子表示)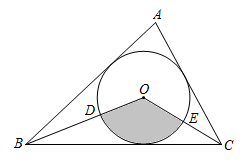 13. 如图,在中, , , , 半径为1的在内平移(可以与该三角形的边相切),则点到上的点的距离的最大值为.
13. 如图,在中, , , , 半径为1的在内平移(可以与该三角形的边相切),则点到上的点的距离的最大值为.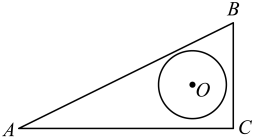 14. 如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A.D是BC边上的动点,当△ACD为直角三角形时,AD的长为
14. 如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A.D是BC边上的动点,当△ACD为直角三角形时,AD的长为 15. 如图, 是 的直径, 是 的切线, 为切点,连接 ,与 交于点 ,连接 .若 ,则 .
15. 如图, 是 的直径, 是 的切线, 为切点,连接 ,与 交于点 ,连接 .若 ,则 . 16. 如图上,O为内心,过点O的直线分别与AC、AB相交于D、E,若DE=CD+BE,则线段CD的长为.
16. 如图上,O为内心,过点O的直线分别与AC、AB相交于D、E,若DE=CD+BE,则线段CD的长为.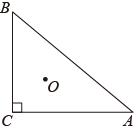
三、解答题(共8题,共72分)
-
17. 如图,AB是⊙O的直径,点E在⊙O上,连接AE和BE,BC平分∠ABE交⊙O于点C,过点C作CD⊥BE,交BE的延长线于点D,连接CE.
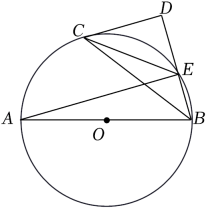 (1)、请判断直线CD与⊙O的位置关系,并说明理由;(2)、若sin∠ECD= , CE=5,求⊙O的半径.18. 已知:如图,AB为⊙O的直径,CD与⊙O相切于点C,交AB延长线于点D,连接AC,BC,∠D=30°,CE平分∠ACB交⊙O于点E,过点B作BF⊥CE,垂足为F.
(1)、请判断直线CD与⊙O的位置关系,并说明理由;(2)、若sin∠ECD= , CE=5,求⊙O的半径.18. 已知:如图,AB为⊙O的直径,CD与⊙O相切于点C,交AB延长线于点D,连接AC,BC,∠D=30°,CE平分∠ACB交⊙O于点E,过点B作BF⊥CE,垂足为F. (1)、求证:CA=CD;(2)、若AB=12,求线段BF的长.19. 如图,以AB为直径的⊙O与△ABC的边BC相切于点B,且与AC边交于点D,点E为BC中点,连接DE、BD.
(1)、求证:CA=CD;(2)、若AB=12,求线段BF的长.19. 如图,以AB为直径的⊙O与△ABC的边BC相切于点B,且与AC边交于点D,点E为BC中点,连接DE、BD.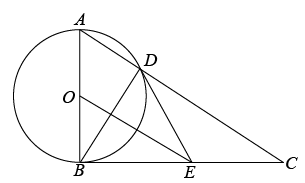 (1)、求证:DE是⊙O的切线;(2)、若DE=5,cos∠ABD= , 求OE的长.20. 如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.
(1)、求证:DE是⊙O的切线;(2)、若DE=5,cos∠ABD= , 求OE的长.20. 如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.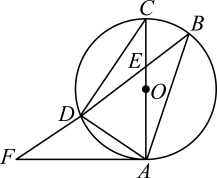 (1)、求证:AF是⊙O的切线;(2)、若⊙O的半径为5,AD是AEF的中线,且AD=6,求AE的长.21. 如图,AB是的直径,AC是的弦,AD平分∠CAB交于点D,过点D作的切线EF,交AB的延长线于点E,交AC的延长线于点F.
(1)、求证:AF是⊙O的切线;(2)、若⊙O的半径为5,AD是AEF的中线,且AD=6,求AE的长.21. 如图,AB是的直径,AC是的弦,AD平分∠CAB交于点D,过点D作的切线EF,交AB的延长线于点E,交AC的延长线于点F. (1)、求证:;(2)、若 , , , 求BE的长.22. 如图,以AB为直径的半圆中,点O为圆心,点C在圆上,过点C作 ,且 .连接AD,分别交 于点E,F,与 交于点G,若 .
(1)、求证:;(2)、若 , , , 求BE的长.22. 如图,以AB为直径的半圆中,点O为圆心,点C在圆上,过点C作 ,且 .连接AD,分别交 于点E,F,与 交于点G,若 . (1)、求证:① ;
(1)、求证:① ;②CD是 的切线.
(2)、求 的值.

