2023年春季浙教版数学九年级下册第一章 《解直角三角形》单元检测B
试卷更新日期:2022-11-20 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为 ,则高BC是( )
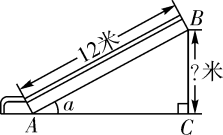 A、 米 B、 米 C、 米 D、 米2. 如图,是的高,若 , , 则边的长为( )
A、 米 B、 米 C、 米 D、 米2. 如图,是的高,若 , , 则边的长为( ) A、 B、 C、 D、3. 如图,在正方形方格纸中,每个小正方形的边长都相等,A,B,C,D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A、 B、 C、 D、3. 如图,在正方形方格纸中,每个小正方形的边长都相等,A,B,C,D都在格点处,AB与CD相交于点P,则cos∠APC的值为( ) A、 B、 C、 D、4. 如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β, , 则建筑物AB的高度为( )
A、 B、 C、 D、4. 如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β, , 则建筑物AB的高度为( ) A、 B、 C、 D、5. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )
A、 B、 C、 D、5. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )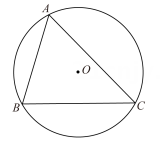 A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)6. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).
A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)6. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).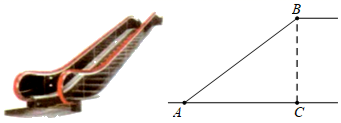 A、7.5米 B、8米 C、9米 D、10米7. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( )
A、7.5米 B、8米 C、9米 D、10米7. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( ) A、 B、 C、 D、8. 如图, 是 的外接圆,CD是 的直径.若 ,弦 ,则 的值为( )
A、 B、 C、 D、8. 如图, 是 的外接圆,CD是 的直径.若 ,弦 ,则 的值为( )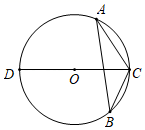 A、 B、 C、 D、9. 如图,等腰△ABC的面积为2 , AB=AC,BC=2.作AE∥BC且AE=BC.点P是线段AB上一动点,连接PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点.那么,当点P从A点运动到B点时,点M的运动路径长为( )
A、 B、 C、 D、9. 如图,等腰△ABC的面积为2 , AB=AC,BC=2.作AE∥BC且AE=BC.点P是线段AB上一动点,连接PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点.那么,当点P从A点运动到B点时,点M的运动路径长为( )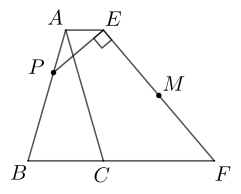 A、 B、3 C、 D、410. 如图,在 中, , , ,将 绕点A逆时针旋转得到 ,使点 落在AB边上,连结 ,则 的值为( )
A、 B、3 C、 D、410. 如图,在 中, , , ,将 绕点A逆时针旋转得到 ,使点 落在AB边上,连结 ,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
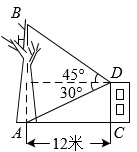
11. 如图,校园内有一株枯死的大树 , 距树12米处有一栋教学楼 , 为了安全,学校决定砍伐该树,站在楼顶处,测得点的仰角为45°,点的俯角为30°,小青计算后得到如下结论:①米;②米;③若直接从点处砍伐,树干倒向教学楼方向会对教学楼有影响;④若第一次在距点的8米处的树干上砍伐,不会对教学楼造成危害.其中正确的是.(填写序号,参考数值: , )
 12. 如图,在矩形中, , 将线段绕点按逆时针方向旋转,使得点落在边上的点处,线段扫过的面积为 .
12. 如图,在矩形中, , 将线段绕点按逆时针方向旋转,使得点落在边上的点处,线段扫过的面积为 .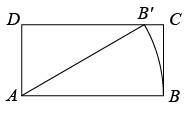 13. 如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔的高度,他从古塔底部点处前行到达斜坡的底部点C处,然后沿斜坡前行到达最佳测量点D处,在点D处测得塔顶A的仰角为 , 已知斜坡的斜面坡度 , 且点A,B,C,D,在同一平面内,小明同学测得古塔的高度是 .
13. 如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔的高度,他从古塔底部点处前行到达斜坡的底部点C处,然后沿斜坡前行到达最佳测量点D处,在点D处测得塔顶A的仰角为 , 已知斜坡的斜面坡度 , 且点A,B,C,D,在同一平面内,小明同学测得古塔的高度是 .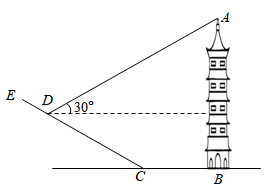 14. 如图,在 中, ,点D、E分别在 、 上,点F在 内.若四边形 是边长为1的正方形,则 .
14. 如图,在 中, ,点D、E分别在 、 上,点F在 内.若四边形 是边长为1的正方形,则 . 15. 如图,从楼顶 处看楼下荷塘 处的俯角为 ,看楼下荷塘 处的俯角为 ,已知楼高 为 米,则荷塘的宽 为米.(结果保留根号)
15. 如图,从楼顶 处看楼下荷塘 处的俯角为 ,看楼下荷塘 处的俯角为 ,已知楼高 为 米,则荷塘的宽 为米.(结果保留根号)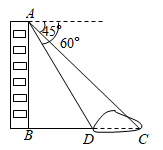 16. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.
16. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.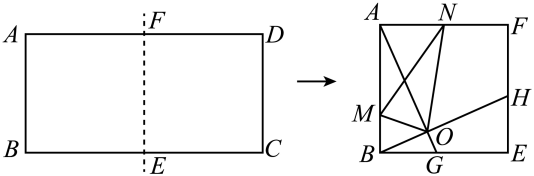
三、解答题(共9题,共72分)
-
17. 计算: .18. 计算:(﹣1)3+| 1|﹣( )﹣2+2cos45° .19. 旗杆及升旗台的剖面如图所示,MN、CD为水平线,旗杆AB⊥CD于点B.某一时刻,旗杆AB的一部分影子BD落在CD上,另一部分影子DE落在坡面DN上,已知BD=1.2m,DE=1.4m.同一时刻,测得竖直立在坡面DN上的1m高的标杆影长为0.25m(标杆影子在坡面DN上),此时光线AE与水平线的夹角为80.5°,求旗杆AB的高度.(参考数据:sin80.5°≈0.98,cos80.5°≈0.17,tan80.5°≈6)
 20. 随着我国科学技术的不断发展,科学幻想变为现实.如图1是我国自主研发的某型号隐形战斗机模型,全动型后掠翼垂尾是这款战斗机亮点之一.图2是垂尾模型的轴切面,并通过垂尾模型的外围测得如下数据, , , , , 且 , 求出垂尾模型ABCD的面积.(结果保留整数,参考数据: , )
20. 随着我国科学技术的不断发展,科学幻想变为现实.如图1是我国自主研发的某型号隐形战斗机模型,全动型后掠翼垂尾是这款战斗机亮点之一.图2是垂尾模型的轴切面,并通过垂尾模型的外围测得如下数据, , , , , 且 , 求出垂尾模型ABCD的面积.(结果保留整数,参考数据: , )
图1 图2
21. 我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔,是苏北地区现存最高和最古老的宝塔.小明与小亮要测量阿育王塔的高度,如图所示,小明在点 处测得阿育王塔最高点 的仰角 ,再沿正对阿育王塔方向前进至 处测得最高点 的仰角 , ;小亮在点 处竖立标杆 ,小亮的所在位置点 、标杆顶 、最高点 在一条直线上, , . (1)、求阿育王塔的高度 ;(2)、求小亮与阿育王塔之间的距离 .
(1)、求阿育王塔的高度 ;(2)、求小亮与阿育王塔之间的距离 .(注:结果精确到 ,参考数据: , , )
22. 小华将一张纸对折后做成的纸飞机如图1,纸飞机机尾的横截面是一个轴对称图形,其示意图如图2,已知AD=BE=10cm,CD=CE=5cm,AD⊥CD,BE⊥CE,∠DCE=40°.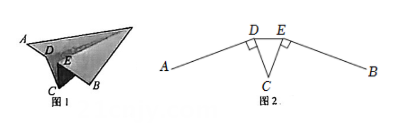 (1)、连结DE,求线段DE的长.(2)、求点A、B之间的距离.
(1)、连结DE,求线段DE的长.(2)、求点A、B之间的距离.(结果精确到0.1cm.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36.sin40°≈0.64.cos40°≈0.77,tan40°≈0.84)
23. 如图,斜坡 的坡角 ,计划在该坡面上安装两排平行的光伏板.前排光伏板的一端位于点 ,过其另一端 安装支架 , 所在的直线垂直于水平线 ,垂足为点 为 与 的交点.已知 ,前排光伏板的坡角 .参考数据:
三角函数锐角
13°
28°
32°
0.22
0.47
0.53
0.97
0.88
0.85
0.23
0.53
0.62
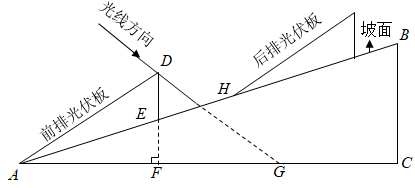 (1)、求 的长(结果取整数);(2)、冬至日正午,经过点 的太阳光线与 所成的角 .后排光伏板的前端 在 上.此时,若要后排光伏板的采光不受前排光伏板的影响,则 的最小值为多少(结果取整数)?24. 某海域有一小岛P,在以P为圆心,半径r为 海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东 的方向上,当海监船行驶 海里后到达B处,此时观测小岛P位于B处北偏东 方向上.
(1)、求 的长(结果取整数);(2)、冬至日正午,经过点 的太阳光线与 所成的角 .后排光伏板的前端 在 上.此时,若要后排光伏板的采光不受前排光伏板的影响,则 的最小值为多少(结果取整数)?24. 某海域有一小岛P,在以P为圆心,半径r为 海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东 的方向上,当海监船行驶 海里后到达B处,此时观测小岛P位于B处北偏东 方向上. (1)、求A,P之间的距离AP;(2)、若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?25. 如图,和的顶点重合, , , , .
(1)、求A,P之间的距离AP;(2)、若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?25. 如图,和的顶点重合, , , , .

 (1)、特例发现:如图1,当点 , 分别在 , 上时,可以得出结论: , 直线与直线的位置关系是;(2)、探究证明:如图2,将图1中的绕点顺时针旋转,使点恰好落在线段上,连接 , (1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)、拓展运用:如图3,将图1中的绕点顺时针旋转 , 连接、 , 它们的延长线交于点 , 当时,求的值.
(1)、特例发现:如图1,当点 , 分别在 , 上时,可以得出结论: , 直线与直线的位置关系是;(2)、探究证明:如图2,将图1中的绕点顺时针旋转,使点恰好落在线段上,连接 , (1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)、拓展运用:如图3,将图1中的绕点顺时针旋转 , 连接、 , 它们的延长线交于点 , 当时,求的值.