2023年中考数学专题训练：数学思想
试卷更新日期：2022-11-19 类型：一轮复习
一、填空题
-
1. 若 ， 均为有理数，且 ，则 ．2. 某餐厅在客人用餐完毕后收拾餐桌分以下几个步骤：①回收餐具与剩菜、清洁桌面；②清洁椅面与地面；③摆放新餐具，前两个步骤顺序可以互换，但摆放新餐具必须在前两个步骤都完成之后才可进行，每个步骤所花费时间如表所示：
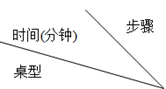
回收餐具与剩菜、清洁桌面
清洁椅面与地面
摆放新餐具
大桌
5
3
2
小桌
3
2
1
现有三名餐厅工作人员分别负责①回收餐具与剩菜、清洁桌面，②清洁椅面与地面，③摆放新餐具，每张桌子同一时刻只允许一名工作人员进行工作，现有两张小桌和一张大桌需要清理，那么将三张桌子收拾完毕最短需要分钟．
3. 已知方程组 的解是 ． 则方程组 的解是 ．4. 为了预防新型冠状病毒的传染，人员之间需要保持一米以上的安全距离．某公司会议室共有四行四列座椅，并且相邻两个座椅之间的距离超过一米，为了保证更加安全，公司规定在此会议室开会时，每一行、每一列均不能有连续三人就座．例如图1中第一列所示情况不满足条件（其中“√”表示就座人员）．根据该公司要求，该会议室最多可容纳的就座人数为人，并在图2中画出一种相应的座位安排示意图．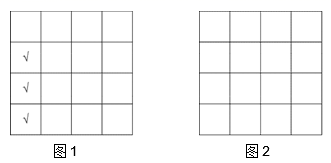
5. 如果∠AOB=34°，∠BOC=18°，那么∠AOC的度数是.6. 若等腰三角形的两边长分别为3cm和6cm，则它的周长为 ．7. 已知一个三角形的三边都是方程 的根，则此三角形的周长为 ．8. 如图，PA，PB是⊙O的切线，切点为A，B，∠P=58°，C是⊙O上异于A，B的点，则∠ACB的度数为 ．
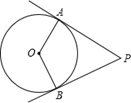9. 已知抛物线 （m为常数）．(1)、若该抛物线经过点（1，m+7），求m的值；(2)、若抛物线上始终存在不重合的两点关于原点对称，求满足条件的最大整数m；(3)、将该抛物线向下平移若干个单位长度，所得的新抛物线经过P（ ， ），Q（7， ）（其中 ）两点，当 时，点P是该部分函数图象的最低点，求m的取值范围．10. 数轴上一点A，一只蚂蚁从A点出发爬了5个单位长度到达了原点，则点A所表示的数是.11. 如图，在Rt△ABC中，∠C=90 ，AC=12cm，BC=6cm，一条线段PQ=AB，P，Q两点分别在线段AC和AC的垂线AX上移动，则当AP= 时，才能使△ABC和△APQ全等．
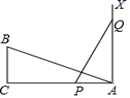12. 如图， 中，CD⊥AB，垂足为D，CD＝BD＝5，AD＝4，点M从点B出发沿线段BA方向运动到点A停止，过点M作MN⊥AB，交折线BC﹣CA于点N，连接DN，AN，若 与 的面积相等，则线段BM的长为 ．
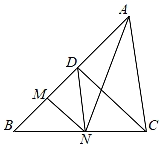13. 三角形中，如果有一个内角是另外一个内角的3倍，我们把这个三角形叫做“三倍角三角形”．在一个“三倍角三角形”中有一个内角为60°，则另外两个角分别为 ．14. 如图，Rt△ABC中，∠C=90°，在△ABC外取点D ， E ， 使AD=AB ， AE=AC ， 且α+β＝∠B ， 连结DE ． 若AB＝4，AC＝3，则DE＝ ．
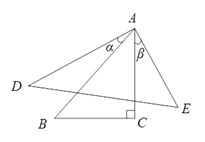15. 某商场在端午节前以1元/个的价格购进1000个粽子，现有以下三种销售方式：不加工直接卖，对产品进行粗加工后再卖，对产品进行精加工后再卖．受加工能力和气温影响，粗加工一天只能加工200个，细加工一天只能加工100个，两种加工不能同时进行，且最多加工三天．加工方式
加工成本
销售单位
售价
直接卖
0
个
2元/个
粗加工
1元/个
包装袋（一袋5个）
30元/袋
精加工
2.5元/个
礼盒（一盒10个）
85元/盒
假设所有粽子均能全部售出，则以下销售方式中利润最大的是 ．
方案一：不加工直接销售；
方案二：三天全部进行精加工，剩下的直接卖；
方案三：两天精加工，一天粗加工，剩下的直接卖；
方案四：两天粗加工，一天精加工，剩下的直接卖．
16. 某快餐店外卖促销，佳佳和点点想点外卖，每单需支付送餐费5元，每种餐食外卖价格如下表：餐食种类
价格（单位：元）
汉堡套餐
40
鸡翅
16
鸡块
15
冰激凌
14
蔬菜沙拉
9
促销活动：
①汉堡套餐5折优惠，每单仅限一套；
②全部商品（包括打折套餐）满20元减4元，满40元减10元，满60元减15元，满80元减20元．
佳佳想要汉堡套餐、鸡翅、冰激凌、蔬菜沙拉各一份；点点想要汉堡套餐、鸡块、冰激凌各一份，若他们把想要的都买全，最少要花元（含送餐费）．
17. 已知y = | x － 1 | x + | x －2 | ( x － 1 )， 则不等式 y < 0的解集为 .18. 在平面直角坐标系xOy中，A（4，0），B（0，3），C（m ， 7），三角形ABC的面积为14，则m的值为 ．19. 如图是一个运算程序的示意图，若输出y的值为2，则输入x的值可能为 ．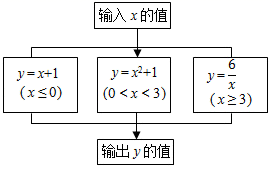
20. 2019年，部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示，某国创新综合排名全球第13，创新效率排名全球第 ．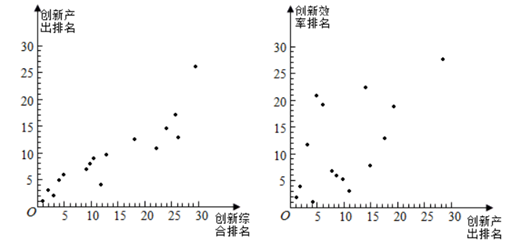
二、解答题
-
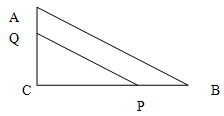
21. 如图 中，∠C=90°，BC = 12cm，AC = 5cm，点P从B出发，沿BC方向以2cm/s的速度移动，点Q从C出发，沿CA方向以1cm/s的速度移动，若P、Q分别同时从B、C出发，经过多少时间 与 相似？
22. “通过等价变换，化陌生为熟悉，化未知为已知”是数学学习中解决问题的基本思维方式，例如：解方程 ，就可以利用该思维方式，设 ，将原方程转化为： 这个熟悉的关于y的一元二次方程，解出y，再求x，这种方法又叫“换元法”．请你用这种思维方式和换元法解决下面的问题．已知实数x，y满足 ，求 的值．23. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．
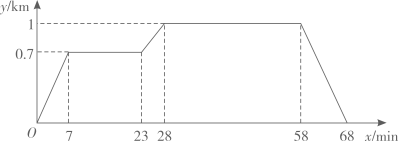
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上，食堂离宿舍 ，图书馆离宿舍 ．周末，小亮从宿舍出发，匀速走了 到食堂；在食堂停留 吃早餐后，匀速走了 到图书馆；在图书馆停留 借书后，匀速走了 返回宿舍，给出的图象反映了这个过程中小亮离宿舍的距离 与离开宿舍的时间 之间的对应关系．
请根据相关信息，解答下列问题：
(1)、填表：离开宿舍的时间/
2
5
20
23
30
离宿舍的距离/
0.2
0.7
(2)、填空：①食堂到图书馆的距离为 ．
②小亮从食堂到图书馆的速度为 ．
③小亮从图书馆返回宿舍的速度为 ．
④当小亮离宿舍的距离为 时，他离开宿舍的时间为 ．
(3)、当 时，请直接写出y关于x的函数解析式．24. 如图
(1)、如图，矩形ABCD的对角线长为a ， 对角线与一边的夹角为α（α≤45°），则CD＝（用α的三角函数和a来表示），S△BCD＝（用α的三角函数和a来表示）＝（用2α的三角函数和a来表示）；(2)、猜想并直接写出sin2α，sinα，cosα之间的数量关系．25. m是什么整数时，方程（m2﹣1）x2﹣6（3m﹣1）x+72＝0有两个不相等的正整数根．26. 已知四边形ABCD是⊙O的内接四边形，∠DAB＝120°，BC＝CD ， AD＝4，AC＝7，求AB的长度．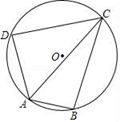
27. 把一张形状是矩形的纸片剪去其中某个角，剩下的部分是一个多边形，则这个多边形的内角和是多少？