2022-2023学年浙教版数学七上期末复习专题 余角、补角
试卷更新日期：2022-11-19 类型：复习试卷
一、单选题（每题3分，共30分）
-
1. 已知∠α＝125°19′，则∠α的补角等于（ ）A、144°41′ B、144°81′ C、54°41′ D、54°81′2. 若一个角比它的余角大30°，则这个角等于（ ）A、30° B、60° C、105° D、120°3. 一个角的度数等于 ， 那么它的余角等于（ ）A、 B、 C、 D、4. 如图，点A，O，B在一条直线上，OE⊥AB于点O，如果∠1与∠2互余，那么图中相等的角有（ ）
A、6对 B、5对 C、4对 D、3对5. 下列说法中，正确的是（ ）A、一个锐角的补角大于这个角的余角 B、一对互补的角中，一定有一个角是锐角 C、锐角的余角一定是钝角 D、锐角的补角一定是锐角6. 如图，点O在直线上， ， 则的大小为（ ）
A、 B、 C、 D、7. 已知∠1和∠2互为余角，且∠2与∠3互补，∠1＝60°，则∠3为（ ）A、120° B、60° C、30° D、150°8. 如果∠1与∠2互补，∠3与∠4互补，且∠1＝∠3，那么（ ）A、∠2＞∠4 B、∠2＜∠4 C、∠2＝∠4 D、∠2与∠4的大小不定9. 如图：O为直线AB上的一点，OC为一条射线，OD平分 ， OE平分 ， 图中互余的角共有（ ）
A、1对 B、2对 C、4对 D、6对10. 已知和互补，且 ， 则有下列式子：①；②；③；④ ． 其中表示的余角的式子有（ ）A、①②③ B、①②④ C、①② D、①③④二、填空题（每题4分，共24分）
-
11. 下列说法正确的有 ． （请将符合题意说法的序号填在横线上）
⑴锐角的补角一定是钝角；
⑵一个角的补角一定大于这个角；
⑶若两个角是同一个角的补角，则它们相等；
⑷锐角和钝角互补．
12. 若 ， ， 则与的关系是 ． （填“互余”或“互补”）13. 已知∠α和∠β互为补角，并且∠β的一半比∠α小30°，则∠α＝ ， ∠β＝ ．14. 已知一个角的补角是它余角的3倍，那么这个角等于°．15. 如果∠α是直角的 ，则∠α的补角是度.16. 已知∠A=32°15′48″，则∠A余角的度数为（用度分秒形式表示）三、解答题（共8题，共66分）
-
17. 如图，平面上有四个点A、B、C、D：
( 1 )根据下列语句画图：
①射线BA；
②直线BD与线段AC相交于点E；
( 2 )图中以E为顶点的角中，请写出∠AED的补角.
18. 如图，点A、O、B在同一条直线上，射线OD平分∠AOC，且∠DOE＝90°．求证：OE平分∠BOC．
19. 已知一个角的余角比这个角的补角的一半还小12°，求这个角的度数．20. 如图，直线 相交于点 平分 ，求 和 的度数.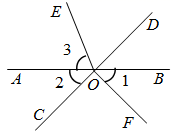
21. 我们规定，如果两个角的差是一个直角，那么这两个角互为足角．其中的一个角叫做另一个角的足角．
(1)、如图，直线经过点O，OE平分 ， ． 请直接写出图中的足角；(2)、如果一个角的足角等于这个角的补角，求这个角的度数．22. 如图，是直线上的一点， ， 、分别是、的平分线．
(1)、图中所有与互余的角有；(2)、图中与互补的角有；(3)、求的度数．23. 已知：∠AOD＝150°，OB，OE，OF是∠AOD内的射线.
(1)、如图1，若OE平分∠AOB，OF平分∠BOD，当∠AOB＝60°时，∠EOF＝；当射线OB绕占O在∠AOD内部旋转时，∠EOF＝.(2)、如图2，若∠BOC＝30°，OE平分∠AOC，OF平分∠BOD，当∠BOC绕点O在∠AOD内旋转时，小明认为∠AOE与∠DOF互余.小明的理由如下：
∵ OE平分∠AOC，
∵ OF平分∠BOD，
∴ ∠DOF＝
（请补充完整理由）
(3)、如图3，当射线OB在∠AOD外，若∠BOC＝30°，OE平分∠AOC，OF平分∠BOD，①当∠AOB小于30°时，猜想∠AOE与∠DOF的关系，并说明理由.
②当∠AOB大干30°而小于180°时，∠EOF＝▲ .
24. 如图1，已知∠AOC＝140°，∠BOC的余角比它的补角的 少 .
(1)、求∠BOC的度数；(2)、如图1，当射线OP从OB处绕点O以4度/秒的速度逆时针旋转，在旋转过程中，保持射线OP始终在∠BOA的内部，当∠POC＝10°时，求旋转时间.(3)、如图2，若射线OD为∠AOC的平分线，当射线OP从OB处绕点O以4度/秒的速度逆时针旋转，同时射线OT从射线OD处以x度/秒的速度绕点O顺时针旋转，当这两条射线重合于射线OE处（OE在∠DOC的内部）时， ，求x的值.（注：本题中所涉及的角都是小于 的角）