2022-2023学年浙教版数学七上期末复习专题 角的度量、大小比较与和差
试卷更新日期:2022-11-19 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 下列角中,能用 , , 三种方法表示同一个角的是( )A、
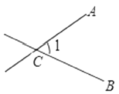 B、
B、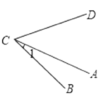 C、
C、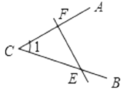 D、
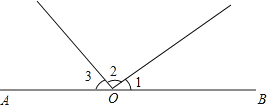
D、 2. 把 用度、分、秒表示,正确的是( )A、 B、 C、 D、3. 如图,从点O出发的5条射线,可以组成的锐角的个数是( )
2. 把 用度、分、秒表示,正确的是( )A、 B、 C、 D、3. 如图,从点O出发的5条射线,可以组成的锐角的个数是( ) A、8 B、9 C、10 D、114. 在同一平面内,已知 , , 则等于( ).A、80° B、40° C、80°或40° D、20°5. 一副三角板如图放置,则∠ABC的度数是( )
A、8 B、9 C、10 D、114. 在同一平面内,已知 , , 则等于( ).A、80° B、40° C、80°或40° D、20°5. 一副三角板如图放置,则∠ABC的度数是( ) A、135° B、120° C、105° D、75°6. 数学课上,老师提出一个问题:经过已知角一边上的点,作一个角等于已知角.如图,用尺规过的边上一点C(图①)作(图②).我们可以通过以下步骤作图:
A、135° B、120° C、105° D、75°6. 数学课上,老师提出一个问题:经过已知角一边上的点,作一个角等于已知角.如图,用尺规过的边上一点C(图①)作(图②).我们可以通过以下步骤作图:①作射线;②以点O为圆心,小于的长为半径作弧,分别交 , 于点N,M;③以点P为圆心,的长为半径作弧,交上一段弧于点Q;④以点C为圆心,的长为半径作弧,交于点P.下列排序正确的是( )
 A、①②③④ B、②④③① C、③②④① D、④③①②7. 嘉淇在用直尺和圆规作一个角等于已知角的步骤如下:
A、①②③④ B、②④③① C、③②④① D、④③①②7. 嘉淇在用直尺和圆规作一个角等于已知角的步骤如下:已知:∠AOB
求作:∠A′O′B′,使∠A′O′B′=∠AOB
作法:⑴如图,以点O为圆心,m为半径画弧,分别交OA,OB于点C,D;
⑵画一条射线O′A′,以点O′为圆心,n为半径画弧,交O′A′于点C′;
⑶以点C′为圆心,p为半径画弧,与第(2)步中所画的弧相交于点D′;
⑷过点D′画射线O′B′,则∠A′O′B′=∠AOB.
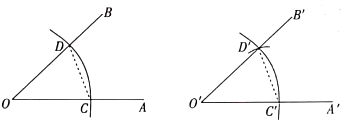
下列说法正确的是( )
A、m=p>0 B、n=p>0 C、p=n>0 D、m=n>08. 如图,∠AOE=100°,∠BOF=80°,OE平分∠BOC,OF平分∠AOC,则∠EOF的度数为( )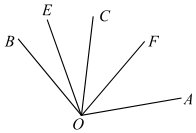 A、40° B、50° C、60° D、70°9. 如图, ,射线OM、ON分别平分 与 , 是直角,则 的度数为( )
A、40° B、50° C、60° D、70°9. 如图, ,射线OM、ON分别平分 与 , 是直角,则 的度数为( )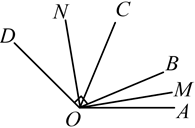 A、70° B、62° C、60° D、58°10. 已知∠AOB,求作射线OC,使OC平分∠AOB作法的合理顺序是( )
A、70° B、62° C、60° D、58°10. 已知∠AOB,求作射线OC,使OC平分∠AOB作法的合理顺序是( )①作射线OC;②在OA和OB上分别截取OD,OE,使OD=OE;
③分别以D,E为圆心,大于DE的长为半径作弧,在∠AOB内,两弧交于C.
A、①②③ B、②①③ C、②③① D、③②①二、填空题(每题4分,共24分)
-
11. 计算:35.1°+40.5°= . (结果用度表示)12. 已知 , 比较这两个角的大小, 结果为∠1∠2.13. 比较图中、的大小:因为和是公共边,在的内部,所以 . (填“>”,“<”或“=”)
 14. 如图所示,图中小于平角的角有个.
14. 如图所示,图中小于平角的角有个.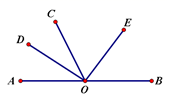 15. 如图,将一副三角板摆放在直线AB上, , ,设 ,则用x的代数式表示 的度数为.
15. 如图,将一副三角板摆放在直线AB上, , ,设 ,则用x的代数式表示 的度数为.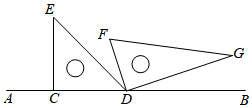 16. 如图,点C,D在线段BE上(C在D的左侧),点A在线段BE外,连接AB,AC,AD,AE,已知∠BAE = 120°,∠CAD = 60°,有下列说法:①直线CD上以B,C,D,E为端点的线段共有6条;②作∠BAM= ∠BAD,∠EAN= ∠EAC.则∠MAN=30°;③以A为顶点的所有小于平角的角的度数和为420°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和最大值为17,最小值为11.其中说法正确的有 .(填上所有正确说法的序号)
16. 如图,点C,D在线段BE上(C在D的左侧),点A在线段BE外,连接AB,AC,AD,AE,已知∠BAE = 120°,∠CAD = 60°,有下列说法:①直线CD上以B,C,D,E为端点的线段共有6条;②作∠BAM= ∠BAD,∠EAN= ∠EAC.则∠MAN=30°;③以A为顶点的所有小于平角的角的度数和为420°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和最大值为17,最小值为11.其中说法正确的有 .(填上所有正确说法的序号)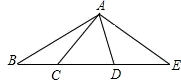
三、解答题(共8题,共66分)
-
17. 计算:(1)、48°39′+67°31′(2)、180°﹣21°17′×518. 作图题(要求:用尺规作图,不写作法,保留作图痕迹).
已知:∠α,∠β,线段c .
求作: ABC , 使∠A=∠α,∠ABC=∠β,AB=2c .
 19.
19.如图,AB是一条直线,如果∠1=65°15′,∠2=78°30′,求∠3的度数.
 20. 如图,点在的边上,选择合适的画图工具按要求画图.,
20. 如图,点在的边上,选择合适的画图工具按要求画图.,
⑴反向延长射线 , 得到射线 , 在射线上取一点 , 使得;
⑵使用量角器,画出的角平分线;
⑶在射线上作一点 , 使得最小;
⑷写出你完成(3)的作图依据: .
21. 如图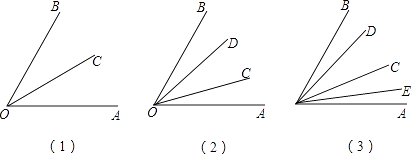 (1)、在∠AOB内部画1条射线OC,则图1中有个不同的角;(2)、在∠AOB内部画2条射线OC,OD,则图2中有个不同的角;(3)、在∠AOB内部画3条射线OC,OD,OE,则图3中有个不同的角;(4)、在∠AOB内部画10条射线OC,OD,OE…,则图中有个不同的角;(5)、在∠AOB内部画n条射线OC,OD,OE…,则图中有个不同的角.22. 如图①,已知OC是∠AOB内部的一条射线,M、N分别为OA、OB上的点,线段OM、ON同时开始旋转,线段OM以30度/秒绕点O逆时针旋转,线段ON以10度/秒的速度绕点O顺时针旋转,当OM旋转到与OB重合时,线段OM、ON都停止旋转.设OM的旋转时间为t秒.
(1)、在∠AOB内部画1条射线OC,则图1中有个不同的角;(2)、在∠AOB内部画2条射线OC,OD,则图2中有个不同的角;(3)、在∠AOB内部画3条射线OC,OD,OE,则图3中有个不同的角;(4)、在∠AOB内部画10条射线OC,OD,OE…,则图中有个不同的角;(5)、在∠AOB内部画n条射线OC,OD,OE…,则图中有个不同的角.22. 如图①,已知OC是∠AOB内部的一条射线,M、N分别为OA、OB上的点,线段OM、ON同时开始旋转,线段OM以30度/秒绕点O逆时针旋转,线段ON以10度/秒的速度绕点O顺时针旋转,当OM旋转到与OB重合时,线段OM、ON都停止旋转.设OM的旋转时间为t秒.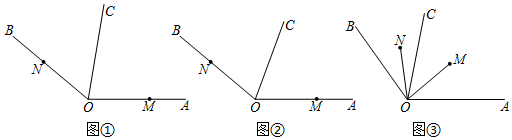 (1)、若∠AOB=140°,当t=2秒时,∠MON= , 当t=4秒时,∠MON=;(2)、如图②,若∠AOB=140°,OC是∠AOB的平分线,求t为何值时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.(3)、如图③,若OM、ON分别在∠AOC、∠COB内部旋转时,总有∠COM=3∠CON,请直接写出 的值.23. 已知 , 为 内部的一条射线, .
(1)、若∠AOB=140°,当t=2秒时,∠MON= , 当t=4秒时,∠MON=;(2)、如图②,若∠AOB=140°,OC是∠AOB的平分线,求t为何值时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.(3)、如图③,若OM、ON分别在∠AOC、∠COB内部旋转时,总有∠COM=3∠CON,请直接写出 的值.23. 已知 , 为 内部的一条射线, . (1)、如图1,若 平分 , 为 内部的一条射线, ,求 的度数;(2)、如图2,若射线 绕着 点从 开始以每秒 的速度顺时针旋转至 结束、 绕着 点从 开始以每秒 的速度逆时针旋转至 结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为 秒,当 时,求 的值;(3)、若射线 绕着 点从 开始以每秒 的速度逆时针旋转至 结束,在旋转过程中, 平分 ,试问 在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及 相应所在的时间段.(本题中的角均为大于 且小于 的角)24. 如图,直线 , 相交于点 , 平分 .
(1)、如图1,若 平分 , 为 内部的一条射线, ,求 的度数;(2)、如图2,若射线 绕着 点从 开始以每秒 的速度顺时针旋转至 结束、 绕着 点从 开始以每秒 的速度逆时针旋转至 结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为 秒,当 时,求 的值;(3)、若射线 绕着 点从 开始以每秒 的速度逆时针旋转至 结束,在旋转过程中, 平分 ,试问 在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及 相应所在的时间段.(本题中的角均为大于 且小于 的角)24. 如图,直线 , 相交于点 , 平分 . (1)、【基础尝试】
(1)、【基础尝试】
如图1,若 ,求 的度数;(2)、【画图探究】
作射线 ,设 ,请你利用图2画出图形,探究 与 之间的关系,结果用含 的代数式表示 .(3)、【拓展运用】
在第(2)题中, 可能和 互补吗?请你作出判断并说明理由.