2022-2023学年浙教版数学七上期末复习专题 线段、直线和直线
试卷更新日期:2022-11-19 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 如图,观察图形,下列结论中不正确的是( )
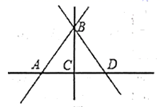 A、图中有 条线段 B、直线 和直线 是同一条直线 C、 D、射线 和射线 是同一条射线2. 木匠在木料上画线,先确定两个点的位置,就能把线画得很准确,其依据是( )A、两点之间线段最短 B、过一点有无数条直线 C、两点确定一条直线 D、两点之间线段的长度叫做这两点之间的距离3. 下列现象中,可用基本事实“两点之间,线段最短”来解释的现象是( )A、用两个钉子就可以把木条固定在墙上 B、把弯曲的公路改直,就能缩短路程 C、锯木料时,一般先在木板上画两点,然后过这两点弹出一条墨迹 D、植树时,只要定出两棵树的位置就能确定同一行树所在的直线4. 下列语句正确的是( )A、延长线段到 , 使 B、反向延长线段 , 得到射线 C、取射线的中点 D、连接A、B两点,使线段过点5. 如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )A、
A、图中有 条线段 B、直线 和直线 是同一条直线 C、 D、射线 和射线 是同一条射线2. 木匠在木料上画线,先确定两个点的位置,就能把线画得很准确,其依据是( )A、两点之间线段最短 B、过一点有无数条直线 C、两点确定一条直线 D、两点之间线段的长度叫做这两点之间的距离3. 下列现象中,可用基本事实“两点之间,线段最短”来解释的现象是( )A、用两个钉子就可以把木条固定在墙上 B、把弯曲的公路改直,就能缩短路程 C、锯木料时,一般先在木板上画两点,然后过这两点弹出一条墨迹 D、植树时,只要定出两棵树的位置就能确定同一行树所在的直线4. 下列语句正确的是( )A、延长线段到 , 使 B、反向延长线段 , 得到射线 C、取射线的中点 D、连接A、B两点,使线段过点5. 如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )A、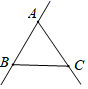 B、
B、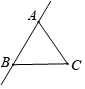 C、
C、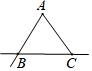 D、
D、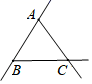 6. 有不在同一直线上的两条线段和 , 李明很难判断出它们的长短,因此他借助于圆规,操作如图所示,由此可得出( )
6. 有不在同一直线上的两条线段和 , 李明很难判断出它们的长短,因此他借助于圆规,操作如图所示,由此可得出( )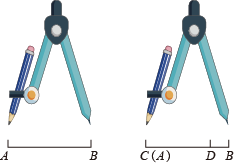 A、 B、 C、 D、无法确定7. A,B,C,D四个村庄之间的道路如图,从A去D有以下四条路线可走,其中路程最短的是( )
A、 B、 C、 D、无法确定7. A,B,C,D四个村庄之间的道路如图,从A去D有以下四条路线可走,其中路程最短的是( )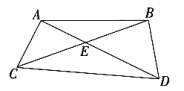 A、A→C→B→D B、A→C→D C、A→E→D D、A→B→D8. 如图,点C、D分别是线段AB上两点(CD>AC,CD>BD),用圆规在线段CD上截取CE=AC,DF=BD, 若点E与点F恰好重合,AB=8,则CD=( )
A、A→C→B→D B、A→C→D C、A→E→D D、A→B→D8. 如图,点C、D分别是线段AB上两点(CD>AC,CD>BD),用圆规在线段CD上截取CE=AC,DF=BD, 若点E与点F恰好重合,AB=8,则CD=( )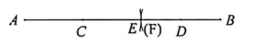 A、4 B、4.5 C、5 D、5.59. 如图所示: 把两个正方形放置在周长为 的长方形 内, 两个正方形的重叠部分的周长为 (图中阴影部分所示), 则这两个正方形的周长和可用代数式表示为( )
A、4 B、4.5 C、5 D、5.59. 如图所示: 把两个正方形放置在周长为 的长方形 内, 两个正方形的重叠部分的周长为 (图中阴影部分所示), 则这两个正方形的周长和可用代数式表示为( )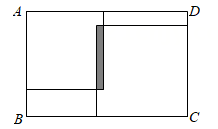 A、 B、 C、 D、10. 已知,点C在直线 AB 上, AC=a , BC=b ,且 a≠b ,点 M是线段 AB 的中点,则线段 MC的长为( )A、 B、 C、 或 D、 或
A、 B、 C、 D、10. 已知,点C在直线 AB 上, AC=a , BC=b ,且 a≠b ,点 M是线段 AB 的中点,则线段 MC的长为( )A、 B、 C、 或 D、 或二、填空题(每题4分,共24分)
-
11. 往返于A、B两地的客车,中途停靠四个站,共有种不同的票价,要准备种车票.12. 王小毛同学做教室卫生时,发现座位很不整齐,他思考了一下,将第一座和最后一座固定之后,沿着第一座最后一座这条线就把座位摆整齐了!他利用了数学原理: .
 13. 已知 三点,过其中每两个点画直线,一共可以画条直线.14. 如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点.点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P最多有个.
13. 已知 三点,过其中每两个点画直线,一共可以画条直线.14. 如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点.点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P最多有个. 15. 如图,两根木条的长度分别为7cm和12cm,在它们的中点处各打一个小孔M、N(木条的厚度,宽度以及小孔大小均忽略不计).将这两根木条的一端重合并放置在同一条直线上,则两小孔间的距离MN=cm.
15. 如图,两根木条的长度分别为7cm和12cm,在它们的中点处各打一个小孔M、N(木条的厚度,宽度以及小孔大小均忽略不计).将这两根木条的一端重合并放置在同一条直线上,则两小孔间的距离MN=cm.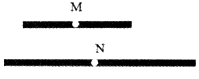 16. 已知点A,B,C都在直线l上,点P是线段AC的中点.设 , ,则线段BC的长为(用含a,b的代数式表示)
16. 已知点A,B,C都在直线l上,点P是线段AC的中点.设 , ,则线段BC的长为(用含a,b的代数式表示)三、解答题(共8题,共66分)
-
17. 如图, 已知在同一平面内的三点
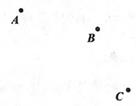
⑴作直线 ,射线 ,线段 ;
⑵在直线 上找一点 , 使线段 的长最小,画出图形,并说明理由.
18. 已知:线段m,n求作:线段AB,使 . 19. 如图,在平面内有三点.
19. 如图,在平面内有三点.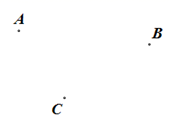 (1)、画直线;画射线;画线段;(2)、在线段上任取一点(不同于),连接 , 并延长至点 , 使;(3)、数一数,此时图中共有多少条线段?多少条射线?20. 已知线段 ,延长线段 到B,使 ,延长 到A,使 ,若 ,求 与 的长.
(1)、画直线;画射线;画线段;(2)、在线段上任取一点(不同于),连接 , 并延长至点 , 使;(3)、数一数,此时图中共有多少条线段?多少条射线?20. 已知线段 ,延长线段 到B,使 ,延长 到A,使 ,若 ,求 与 的长.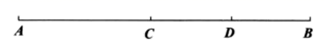 21. 如图所示,已知线段AB,延长AB至点C,使BC=AB;延长BA至点D,使AD=2AB,点E是DB的中点.
21. 如图所示,已知线段AB,延长AB至点C,使BC=AB;延长BA至点D,使AD=2AB,点E是DB的中点. (1)、画出图形,标明C,D,E的位置.(2)、若AE=2,求CD的长.22. 点A,B,C在同一直线上,(1)、若AB=8,AC:BC=3:1,求线段AC的长度;(2)、若AB=m,AC:BC=n:1(n为大于1的整数),求线段AC的长度.23. 如图
(1)、画出图形,标明C,D,E的位置.(2)、若AE=2,求CD的长.22. 点A,B,C在同一直线上,(1)、若AB=8,AC:BC=3:1,求线段AC的长度;(2)、若AB=m,AC:BC=n:1(n为大于1的整数),求线段AC的长度.23. 如图 (1)、【观察思考】如图线段AB上有两个点C、D,分别以点A、B、C、D为端点的线段共有条(2)、【模型构建】若线段上有m个点(包括端点),则该线段上共有条线段(3)、【拓展应用】若有8位同学参加班级的演讲比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),请你应用上述模型构建,求一共要进行多少场比赛?24. 如图1,已知数轴上有三个点A,B,C,它们对应的数分别为 , 且 , 点C对应的数是10.(1)、若BC=15,求
(1)、【观察思考】如图线段AB上有两个点C、D,分别以点A、B、C、D为端点的线段共有条(2)、【模型构建】若线段上有m个点(包括端点),则该线段上共有条线段(3)、【拓展应用】若有8位同学参加班级的演讲比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),请你应用上述模型构建,求一共要进行多少场比赛?24. 如图1,已知数轴上有三个点A,B,C,它们对应的数分别为 , 且 , 点C对应的数是10.(1)、若BC=15,求图1
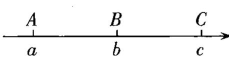 (2)、如图2,在(1)的条件下,O为原点,动点P,Q分别从点A,C同时出发,点P向左运动,运动速度为每秒2个单位长度,点Q向右运动,运动速度为每秒1个单位长度,N为OP的中点,M为BQ的中点.
(2)、如图2,在(1)的条件下,O为原点,动点P,Q分别从点A,C同时出发,点P向左运动,运动速度为每秒2个单位长度,点Q向右运动,运动速度为每秒1个单位长度,N为OP的中点,M为BQ的中点.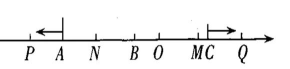 图2
图2用含t的代数式表示PQ,MN.
在点P,Q的运动过程中,PQ与MN存在一个确定的等量关系,请指出它们之间的关系,并说明理由.