2023年春季浙教版数学九年级下册第一章 《解直角三角形》单元检测A
试卷更新日期:2022-11-19 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 某简易房的示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AC的长为( )
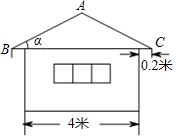 A、米 B、米 C、米 D、米2. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( )
A、米 B、米 C、米 D、米2. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( ) A、 B、 C、 D、3. 在中, , 如果 , 那么的值为( )A、 B、 C、 D、4. 在中,、均为锐角,且 , 则是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形5. 若用我们数学课本上采用的科学计算器计算 , 按键顺序正确的是( )A、
A、 B、 C、 D、3. 在中, , 如果 , 那么的值为( )A、 B、 C、 D、4. 在中,、均为锐角,且 , 则是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形5. 若用我们数学课本上采用的科学计算器计算 , 按键顺序正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,10时到达B处(如图).从A,B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么船在B处时与小岛M的距离( )
6. 上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,10时到达B处(如图).从A,B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么船在B处时与小岛M的距离( )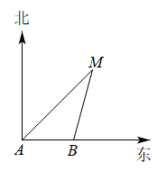 A、海里 B、海里 C、40海里 D、海里7. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )
A、海里 B、海里 C、40海里 D、海里7. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )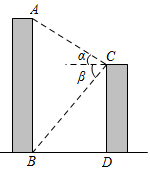 A、 B、 C、 D、8. 如图,是线段AB在投影面P上的正投影, , , 则投影的长为( )
A、 B、 C、 D、8. 如图,是线段AB在投影面P上的正投影, , , 则投影的长为( ) A、 B、 C、 D、9. 小明去爬山,在山脚看山顶角度为30°,小明在坡比为5∶12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )
A、 B、 C、 D、9. 小明去爬山,在山脚看山顶角度为30°,小明在坡比为5∶12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( ) A、(600-250)米 B、(600-250)米 C、(350+350)米 D、500米10. 某限高曲臂道路闸口如图所示,垂直地面于点 , 与水平线的夹角为 , , 若米,米,车辆的高度为(单位:米),不考虑闸口与车辆的宽度:
A、(600-250)米 B、(600-250)米 C、(350+350)米 D、500米10. 某限高曲臂道路闸口如图所示,垂直地面于点 , 与水平线的夹角为 , , 若米,米,车辆的高度为(单位:米),不考虑闸口与车辆的宽度:①当时,小于3.4米的车辆均可以通过该闸口;②当时,等于3.0米的车辆不可以通过该闸口;③当时,等于3.2米的车辆可以通过该闸口.

上述说法正确的个数为( )
A、0个 B、1个 C、2个 D、3个二、填空题(每题3分,共18分)
-
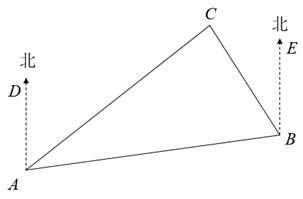
11. 如图, 岛在A岛的北偏东 方向, 岛在 岛的北偏西 方向,则 的大小是.
 12. 北京冬奥会开幕式的巨型雪花状主火炬塔的设计,体现了环保低碳理念.如图所示,它的主体形状呈正六边形.若点A,F,B,D,C,E是正六边形的六个顶点,则tan∠ABE= .
12. 北京冬奥会开幕式的巨型雪花状主火炬塔的设计,体现了环保低碳理念.如图所示,它的主体形状呈正六边形.若点A,F,B,D,C,E是正六边形的六个顶点,则tan∠ABE= . 13. 在中, , 分别为的对边,若 , 则的值为.14. 如图,CD是平面镜,光线从A点出发经CD上点O反射后照射到B点,若入射角为α,反射角为β(反射角等于入射角),AC⊥CD于点C,BD⊥CD于点D,且AC=3,BD=6,CD=12,则tanα的值为 .
13. 在中, , 分别为的对边,若 , 则的值为.14. 如图,CD是平面镜,光线从A点出发经CD上点O反射后照射到B点,若入射角为α,反射角为β(反射角等于入射角),AC⊥CD于点C,BD⊥CD于点D,且AC=3,BD=6,CD=12,则tanα的值为 .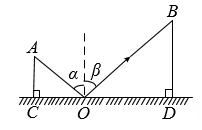 15. 如图,B为地面上一点,测得B到树底部C的距离为 , 在B处放置高的测角仪 , 测得树顶A的仰角为 , 则树高为m(结果保留根号).
15. 如图,B为地面上一点,测得B到树底部C的距离为 , 在B处放置高的测角仪 , 测得树顶A的仰角为 , 则树高为m(结果保留根号). 16. 回雁峰座落于衡阳雁峰公园,为衡山七十二峰之首.王安石曾赋诗联“万里衡阳雁,寻常到此回”.峰前开辟的雁峰广场中心建有大雁雕塑,为衡阳市城徽.某课外实践小组为测量大雁雕塑的高度,利用测角仪及皮尺测得以下数据:如图, , , .已知测角仪 的高度为 ,则大雁雕塑 的高度约为 .(结果精确到 .参考数据: )
16. 回雁峰座落于衡阳雁峰公园,为衡山七十二峰之首.王安石曾赋诗联“万里衡阳雁,寻常到此回”.峰前开辟的雁峰广场中心建有大雁雕塑,为衡阳市城徽.某课外实践小组为测量大雁雕塑的高度,利用测角仪及皮尺测得以下数据:如图, , , .已知测角仪 的高度为 ,则大雁雕塑 的高度约为 .(结果精确到 .参考数据: )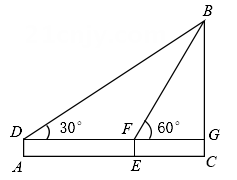
三、解答题(共9题,共72分)
-
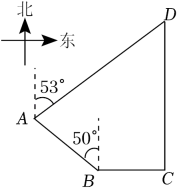
17. 计算: .18. 计算:.19. 如图,我国某海域有A,B,C三个港口,B港口在C港口正西方向33.2nmile(nmile是单位“海里”的符号)处,A港口在B港口北偏西50°方向且距离B港口40nmile处,在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船,求货船与A港口之间的距离.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
 20. 北京时间2022年4月16日9时56分,神舟十三号载人飞船返回舱成功着陆.为弘扬航天精神,某校在教学楼上悬挂了一幅长为的励志条幅(即).小亮同学想知道条幅的底端到地面的距离,他的测量过程如下:如图,首先他站在楼前点处,在点正上方点处测得条幅顶端的仰角为 , 然后向教学楼条幅方向前行到达点处(楼底部点与点 , 在一条直线上),在点正上方点处测得条幅底端的仰角为 , 若 , 均为(即四边形为矩形),请你帮助小亮计算条幅底端到地面的距离的长度.(结果精确到 , 参考数据: , , )
20. 北京时间2022年4月16日9时56分,神舟十三号载人飞船返回舱成功着陆.为弘扬航天精神,某校在教学楼上悬挂了一幅长为的励志条幅(即).小亮同学想知道条幅的底端到地面的距离,他的测量过程如下:如图,首先他站在楼前点处,在点正上方点处测得条幅顶端的仰角为 , 然后向教学楼条幅方向前行到达点处(楼底部点与点 , 在一条直线上),在点正上方点处测得条幅底端的仰角为 , 若 , 均为(即四边形为矩形),请你帮助小亮计算条幅底端到地面的距离的长度.(结果精确到 , 参考数据: , , )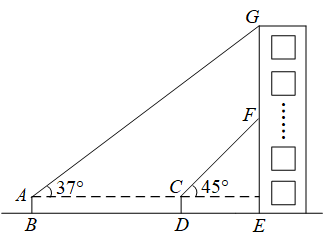 21. 某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆的AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE, CD = 1.6m,BC =5CD.
21. 某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆的AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE, CD = 1.6m,BC =5CD.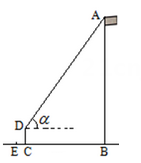 (1)、求BC的长;(2)、从条件①、条件②这两个条件中选择一个作为已知,
(1)、求BC的长;(2)、从条件①、条件②这两个条件中选择一个作为已知,求旗杆AB的高度.
条件①:CE = 1.0m; 条件②:从D处看旗杆顶部A的仰角为54.46°.
注:如果选择条件①和条件②分别作答,按第一个解答计分.参考数据:sin54.46°≈0.81, cos54.46°≈0.58, tan54.46°≈1.40 .
22. 知识小提示:要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角 一般要满足 .如图,现有一架长 的梯子 斜靠在一竖直的墙 上.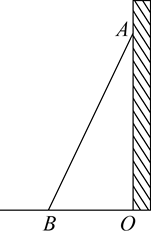
(参考数据: , , , , , , , , )
(1)、当人安全使用这架梯子时,求梯子顶端 与地面距离的最大值;(2)、当梯子底端 距离墙面 时,计算 等于多少度?并判断此时人是否能安全使用这架梯子?23. 如图,某水渠的横断面是以AB为直径的半圆O , 其中水面截线 .嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°,点M的俯角为7°.已知爸爸的身高为1.7m .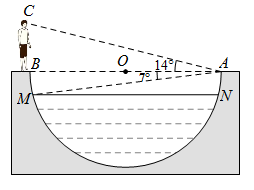 (1)、求∠C的大小及AB的长;(2)、请在图中画出线段DH , 用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).(参考数据: 取4, 取4.1)24. 湖中小岛上码头C处一名游客突发疾病,需要救援.位于湖面B点处的快艇和湖岸 A处的救援船接到通知后立刻同时出发前往救援.计划由快艇赶到码头 C 接该游客,再沿 CA方向行驶,与救援船相遇后将该游客转运到救援船上.已知 C 在A的北偏东 30°方向上,B在A的北偏东 60°方向上,且在C的正南方向 900米处.
(1)、求∠C的大小及AB的长;(2)、请在图中画出线段DH , 用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).(参考数据: 取4, 取4.1)24. 湖中小岛上码头C处一名游客突发疾病,需要救援.位于湖面B点处的快艇和湖岸 A处的救援船接到通知后立刻同时出发前往救援.计划由快艇赶到码头 C 接该游客,再沿 CA方向行驶,与救援船相遇后将该游客转运到救援船上.已知 C 在A的北偏东 30°方向上,B在A的北偏东 60°方向上,且在C的正南方向 900米处.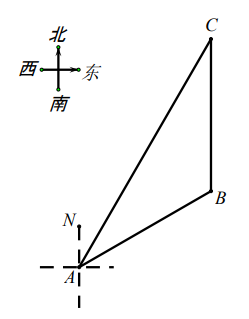 (1)、求湖岸 A 与码头 C 的距离(结果精确到 1 米,参考数据: =1.732 );(2)、救援船的平均速度为 150 米/分,快艇的平均速度为 400 米/分,在接到通知后,快艇能否在5分钟内将该游客送上救援船?请说明理由.(接送游客上下船的时间忽略不计)25. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
(1)、求湖岸 A 与码头 C 的距离(结果精确到 1 米,参考数据: =1.732 );(2)、救援船的平均速度为 150 米/分,快艇的平均速度为 400 米/分,在接到通知后,快艇能否在5分钟内将该游客送上救援船?请说明理由.(接送游客上下船的时间忽略不计)25. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.∵ ,
∴ ,
∴
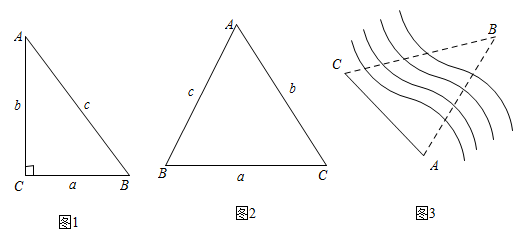 (1)、拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究 , , 之间的关系,并写出探究过程.(2)、解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.
(1)、拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究 , , 之间的关系,并写出探究过程.(2)、解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.