2023年春季北师版数学九年级下册第三章 《圆》单元检测B
试卷更新日期:2022-11-19 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 如图,点 在 上, ,则 ( )
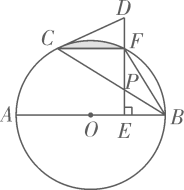
 A、 B、 C、 D、2. 工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A、 B、 C、 D、2. 工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( ) A、10cm B、15cm C、20cm D、24cm3. 如图,已知AB是⊙O的直径,CD是OO的弦,AB⊥CD.垂足为E.若AB=26,CD=24,则∠OCE的余弦值为( )
A、10cm B、15cm C、20cm D、24cm3. 如图,已知AB是⊙O的直径,CD是OO的弦,AB⊥CD.垂足为E.若AB=26,CD=24,则∠OCE的余弦值为( )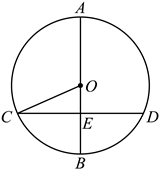 A、 B、 C、 D、4. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )
A、 B、 C、 D、4. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )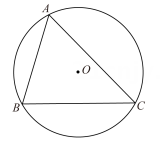 A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)5. 如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是( )
A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)5. 如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是( )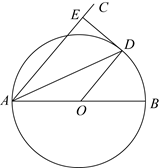 A、AE⊥DE B、AE//OD C、DE=OD D、∠BOD=50°6. 如图,四边形 内接于 ,连接 , , ,若 ,则 ( )
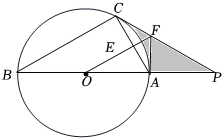
A、AE⊥DE B、AE//OD C、DE=OD D、∠BOD=50°6. 如图,四边形 内接于 ,连接 , , ,若 ,则 ( )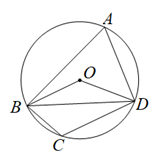 A、 B、 C、 D、7. 如图,点 是 的内心, 的延长线和 的外接圆相交于点 ,与 相交于点 ,则下列结论:① ;②若 ,则 ;③若点 为 的中点,则 ;④ .其中一定正确的个数是( )
A、 B、 C、 D、7. 如图,点 是 的内心, 的延长线和 的外接圆相交于点 ,与 相交于点 ,则下列结论:① ;②若 ,则 ;③若点 为 的中点,则 ;④ .其中一定正确的个数是( )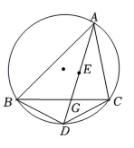 A、1 B、2 C、3 D、48. 如图,边长为的正方形内接于 , , 分别与相切于点和点 , 的延长线与的延长线交于点 , 则图中阴影部分的面积为( )
A、1 B、2 C、3 D、48. 如图,边长为的正方形内接于 , , 分别与相切于点和点 , 的延长线与的延长线交于点 , 则图中阴影部分的面积为( ) A、 B、 C、 D、9. 如图,、分别与相切于点、 , 连接并延长与交于点、 , 若 , , 则的值为( )
A、 B、 C、 D、9. 如图,、分别与相切于点、 , 连接并延长与交于点、 , 若 , , 则的值为( ) A、 B、 C、 D、10. 如图,在 中, ,将 绕点A逆时针旋转 ,得到 ,连接 并延长交AB于点D,当 时, 的长是( )
A、 B、 C、 D、10. 如图,在 中, ,将 绕点A逆时针旋转 ,得到 ,连接 并延长交AB于点D,当 时, 的长是( )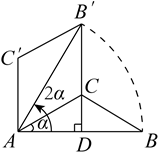 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
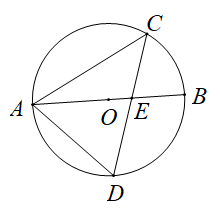
11. 如图,AB是 的直径,弦CD交AB于点E,连接AC,AD.若 ,则 °
 12. 如图,内接于是直径,过点A作的切线 . 若 , 则的度数是度.
12. 如图,内接于是直径,过点A作的切线 . 若 , 则的度数是度.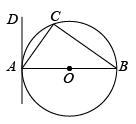 13. 如图,在矩形ABCD中,AD=2 , DC=4 , 将线段DC绕点D按逆时针方向旋转,当点C的对应点E恰好落在边AB上时,图中阴影部分的面积是 .
13. 如图,在矩形ABCD中,AD=2 , DC=4 , 将线段DC绕点D按逆时针方向旋转,当点C的对应点E恰好落在边AB上时,图中阴影部分的面积是 .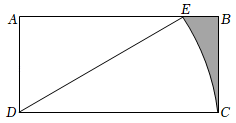 14. 如图,射线AB与⊙O相切于点B,经过圆心O的射线AC与⊙O相交于点D、C,连接BC,若∠A=40°,则∠ACB=.
14. 如图,射线AB与⊙O相切于点B,经过圆心O的射线AC与⊙O相交于点D、C,连接BC,若∠A=40°,则∠ACB=. 15. 如图,在边长为1的正方形网格中,⊙O是△ABC的外接圆,点A,B,O在格点上,则cos∠ACB的值是 .
15. 如图,在边长为1的正方形网格中,⊙O是△ABC的外接圆,点A,B,O在格点上,则cos∠ACB的值是 .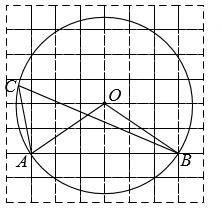 16. 如图,已知AB是⊙O的弦,∠AOB=120°,OC⊥AB,垂足为C,OC的延长线交⊙O于点D.若∠APD是 所对的圆周角,则∠APD的度数是
16. 如图,已知AB是⊙O的弦,∠AOB=120°,OC⊥AB,垂足为C,OC的延长线交⊙O于点D.若∠APD是 所对的圆周角,则∠APD的度数是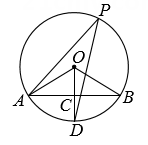
三、解答题(共8题,共72分)
-
17. 如图,四边形内接于圆 , 是圆的直径, , 的延长线交于点 , 延长交于点 , .
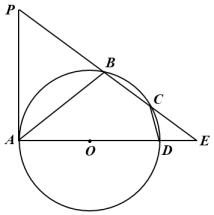 (1)、求证:是圆的切线;(2)、连接 , , , 的长为 .18. 如图, 是 的外接圆,AB是直径, ,连接AD, ,AC与OD相交于点E.
(1)、求证:是圆的切线;(2)、连接 , , , 的长为 .18. 如图, 是 的外接圆,AB是直径, ,连接AD, ,AC与OD相交于点E. (1)、求证:AD是 的切线;(2)、若 , ,求 的半径.19. 如图,在中,以AB为直径作交AC、BC于点D、E,且D是AC的中点,过点D作于点G,交BA的延长线于点H.
(1)、求证:AD是 的切线;(2)、若 , ,求 的半径.19. 如图,在中,以AB为直径作交AC、BC于点D、E,且D是AC的中点,过点D作于点G,交BA的延长线于点H.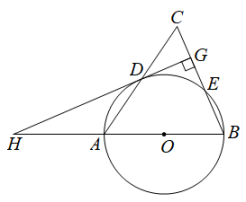 (1)、求证:直线HG是的切线;(2)、若 , 求CG的长.20. 如图,为的直径,点C为上一点,于点D,平分 .
(1)、求证:直线HG是的切线;(2)、若 , 求CG的长.20. 如图,为的直径,点C为上一点,于点D,平分 .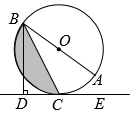 (1)、求证:直线是的切线;(2)、若的半径为2,求图中阴影部分的面积.21. 图,在中, , 点D是边的中点,点O在边上,⊙经过点C且与边相切于点E,.
(1)、求证:直线是的切线;(2)、若的半径为2,求图中阴影部分的面积.21. 图,在中, , 点D是边的中点,点O在边上,⊙经过点C且与边相切于点E,.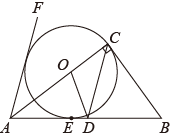 (1)、求证:是⊙的切线;(2)、若 , , 求⊙的半径及的长.22. 如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线,以O为圆心,OC为半径作⊙O与直线AO交于点E和点D.
(1)、求证:是⊙的切线;(2)、若 , , 求⊙的半径及的长.22. 如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线,以O为圆心,OC为半径作⊙O与直线AO交于点E和点D.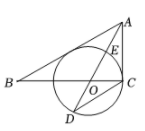 (1)、求证:AB是⊙O的切线;(2)、连接CE,求证:△ACE∽△ADC;(3)、若= , ⊙O的半径为6,求tan∠OAC.
(1)、求证:AB是⊙O的切线;(2)、连接CE,求证:△ACE∽△ADC;(3)、若= , ⊙O的半径为6,求tan∠OAC.