2023年春季北师版数学九年级下册第三章 《圆》单元检测A
试卷更新日期:2022-11-19 类型:单元试卷
一、单选题(每题3分,共30分)
-
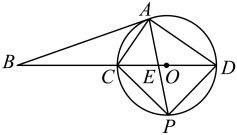
1. 如图, 内接于 ,CD是 的直径, ,则 ( )
 A、70° B、60° C、50° D、40°2. 如图,为的直径,弦交于点 , , , , 则( )
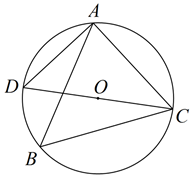
A、70° B、60° C、50° D、40°2. 如图,为的直径,弦交于点 , , , , 则( )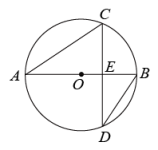 A、 B、 C、1 D、23. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )
A、 B、 C、1 D、23. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )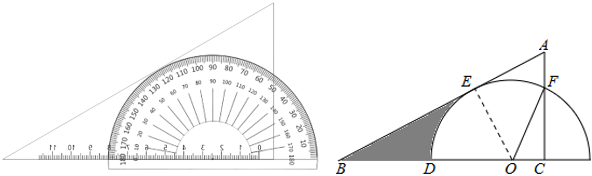 A、 B、 C、 D、4. 我国魏晋时期的数学家刘徽首创割圆术:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣",即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,…….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长 , 则 . 再利用圆的内接正十二边形来计算圆周率则圆周率约为( )
A、 B、 C、 D、4. 我国魏晋时期的数学家刘徽首创割圆术:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣",即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,…….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长 , 则 . 再利用圆的内接正十二边形来计算圆周率则圆周率约为( )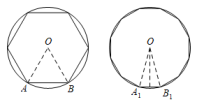 A、 B、 C、 D、5. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )
A、 B、 C、 D、5. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )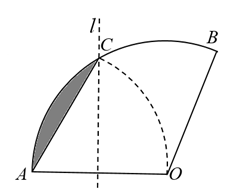 A、 B、 C、 D、6. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A、 B、 C、 D、6. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )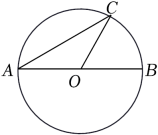 A、6π B、2π C、π D、π7. 如图所示,已知三角形为直角三角形,为圆切线,为切点,则和面积之比为( )
A、6π B、2π C、π D、π7. 如图所示,已知三角形为直角三角形,为圆切线,为切点,则和面积之比为( )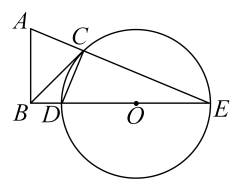 A、 B、 C、 D、8. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( )
A、 B、 C、 D、8. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( ) A、 B、 C、 D、9. 如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为( )
A、 B、 C、 D、9. 如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为( )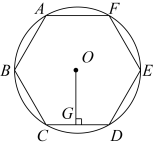 A、3 B、 C、 D、310. 如图,是的直径,点P在的延长线上,与相切于点A,连接 , 若 , 则的度数为( )
A、3 B、 C、 D、310. 如图,是的直径,点P在的延长线上,与相切于点A,连接 , 若 , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,在中,半径垂直弦于点 , 若 , , 则 .
 12. 如图,AB切⊙O于点 , AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为 .
12. 如图,AB切⊙O于点 , AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为 .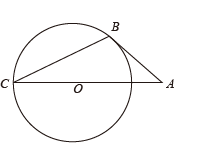 13. 已知⊙O的直径AB长为2,弦AC长为 , 那么弦AC所对的圆周角的度数等于 .14. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.
13. 已知⊙O的直径AB长为2,弦AC长为 , 那么弦AC所对的圆周角的度数等于 .14. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.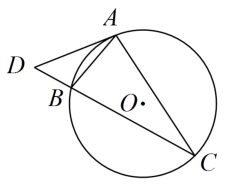 15. 如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=72°,那么∠BOD的度数为 .
15. 如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=72°,那么∠BOD的度数为 .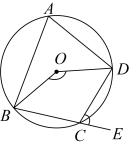 16. 如图,边长为4的正方形ABCD的对角线交于点O,以OC为半径的扇形的圆心角 . 则图中阴影部分面积是 .
16. 如图,边长为4的正方形ABCD的对角线交于点O,以OC为半径的扇形的圆心角 . 则图中阴影部分面积是 .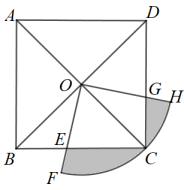
三、解答题(共8题,共72分)
-
17. 如图,在中, , 以AB为直径作⊙ , 分别交BC于点D,交AC于点E, , 垂足为H,连接DE并延长交BA的延长线于点F.
 (1)、求证:DH是⊙的切线;(2)、若E为AH的中点,求的值.18. 如图,AB是半圆O的直径,点C在半圆O上,点D为的中点,连接AC,BC,AD,AD与BC相交于点G,过点D作直线DEBC,交AC的延长线于点E.
(1)、求证:DH是⊙的切线;(2)、若E为AH的中点,求的值.18. 如图,AB是半圆O的直径,点C在半圆O上,点D为的中点,连接AC,BC,AD,AD与BC相交于点G,过点D作直线DEBC,交AC的延长线于点E.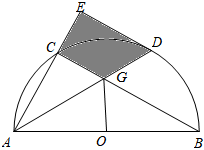 (1)、求证:DE是⊙O的切线;(2)、若 , CG=2 , 求阴影部分的面积.19. 如图,已知BC为⊙O的直径,点D为的中点,过点D作DG∥CE,交BC的延长线于点A,连接BD,交CE于点F.
(1)、求证:DE是⊙O的切线;(2)、若 , CG=2 , 求阴影部分的面积.19. 如图,已知BC为⊙O的直径,点D为的中点,过点D作DG∥CE,交BC的延长线于点A,连接BD,交CE于点F.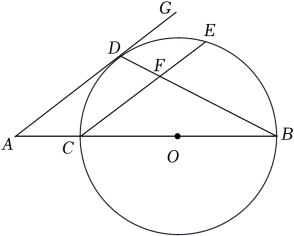 (1)、求证:AD是⊙O的切线;(2)、若EF=3,CF=5,tan∠GDB=2,求AC的长.20. 如图,在Rt△ABC中,∠B=90°,AE平分∠BAC交BC于点E,O为AC上一点,经过点A、E的⊙O分别交AB、AC于点D、F,连接OD交AE于点M.
(1)、求证:AD是⊙O的切线;(2)、若EF=3,CF=5,tan∠GDB=2,求AC的长.20. 如图,在Rt△ABC中,∠B=90°,AE平分∠BAC交BC于点E,O为AC上一点,经过点A、E的⊙O分别交AB、AC于点D、F,连接OD交AE于点M. (1)、求证:BC是⊙O的切线.(2)、若CF=2,sinC= , 求AE的长.21. 如图,四边形内接于 , 为的直径,平分 , 点E在的延长线上,连接 .
(1)、求证:BC是⊙O的切线.(2)、若CF=2,sinC= , 求AE的长.21. 如图,四边形内接于 , 为的直径,平分 , 点E在的延长线上,连接 . (1)、求直径的长;(2)、若 , 计算图中阴影部分的面积.22. 如图,以线段为直径作 , 交射线于点 , 平分交于点 , 过点作直线于点 , 交的延长线于点 . 连接并延长交于点 .
(1)、求直径的长;(2)、若 , 计算图中阴影部分的面积.22. 如图,以线段为直径作 , 交射线于点 , 平分交于点 , 过点作直线于点 , 交的延长线于点 . 连接并延长交于点 .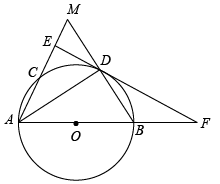 (1)、求证:直线是的切线;(2)、求证:;(3)、若 , , 求的长.
(1)、求证:直线是的切线;(2)、求证:;(3)、若 , , 求的长.