2022-2023学年浙教版数学八上期末复习专题一次函数的应用

试卷更新日期：2022-11-19 类型：复习试卷

进入出卷网下载

一、单选题（每题2分，共20分）

1. 如图，一次函数y＝ax+b的图象与y＝cx+d的图象如图所示且交点的横坐标为4，则下列说法正确的个数是（　　）

①对于函数y＝ax+b来说，y随x的增大而减小；②函数y＝ax+d不经过第一象限；③方程ax+b=cx+d的解是x=4；④ d-b=4（a-c）.

A、1 B、2 C、3 D、4

查看试题解析
2. 如图，直线l是一次函数 $y = k x + b$ 的图象，下列说法中，错误的是（）

A、 $k < 0$ ， $b > 0$ B、若点（－1， $y_{1}$ ）和点（2， $y_{2}$ ）是直线l上的点，则 $y_{1} < y_{2}$ C、若点（2，0）在直线l上，则关于x的方程 $k x + b = 0$ 的解为 $x = 2$ D、将直线l向下平移b个单位长度后，所得直线的解析式为 $y = k x$

查看试题解析
3. 如图，函数 $y = 2 x$ 和 $y = a x + 4$ 的图象相交于点 $A (\frac{3}{2} ， 3)$ ，则不等式 $2 x < a x + 4$ 的解集为（）

A、 $x < \frac{3}{2}$ B、 $x < 3$ C、 $x > \frac{3}{2}$ D、 $x > 3$

查看试题解析
4. 如图，观察图象，可以得出不等式组 ${\begin{array}{l} 3 x + 1 > 0 \\ 0.5 x - 1 < 0 \end{array}$ 的解集是（）

A、 $x < \frac{1}{3}$ B、 $- \frac{1}{3} < x < 0$ C、0＜x＜2 D、 $- \frac{1}{3} < x < 2$

查看试题解析
5. 如果一次函数y＝3x＋6与y＝2x－4的图象交点坐标为（a，b），则 ${\begin{array}{l} x = a \\ y = b \end{array}$ 是方程组（）的解

A、 ${\begin{array}{l} y - 3 x = 6 \\ 2 x + y = - 4 \end{array}$ B、 ${\begin{array}{l} 3 x + 6 + y = 0 \\ 2 x - 4 - y = 0 \end{array}$ C、 ${\begin{array}{l} 3 x - y = - 6 \\ 2 x - 4 - y = 0 \end{array}$ D、 ${\begin{array}{l} 3 x - y = 6 \\ 2 x - y = 4 \end{array}$

查看试题解析
6. 如图，直线 $l_{1} ： y = 3 x + 1$ 与直线 $l_{2} ： y = m x + n$ 相交于点 $P (1 ， b)$ ，则关于x，y的方程组 ${\begin{array}{l} y = 3 x + 1 \\ y = m x + n \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 1 \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 2.5 \end{array}$

查看试题解析
7. 一辆轿车和一辆货车分别从甲、乙两地同时出发，匀速相向而行，相遇后继续前行，已知两车相遇时轿车比货车多行驶了90千米，设行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系，根据图象提供的信息，以下选项中正确的个数是（）
①甲乙两地的距离为450千米；②轿车的速度为70千米/小时；③货车的速度为60千米/小时；④点C的实际意义是轿车出发5小时后到达乙地，此时两车间的距离为300千米．

A、1 B、2 C、3 D、4

查看试题解析
8. 漏刻是我国古代的一种计时工具，据史书记载，西周时期就已经出现了漏刻，这是中国古代人民对函数思想的创造性应用，小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型，研究中发现水位h(cm)是时间t(min)的一次函数，如下表是小明记录的部分数据，其中有一个h的值记录不符合题意，请排除后利用正确的数据确定当时间t为8时，对应的高度h为（）
t（min）
……
0
1
2
3
……
h（cm）
……
0.7
1.2
1.5
1.9
……

A、3.3 B、3.65 C、3.9 D、4.7

查看试题解析
9. 某品牌鞋子的长度ycm与鞋子的“码”数x之间满足一次函数关系．若22码鞋子的长度为16cm，44码鞋子的长度为27cm，则38码鞋子的长度为（）

A、23cm B、24cm C、25cm D、26cm

查看试题解析
10. 在数轴上，点 $A$ 表示－2，点 $B$ 表示 $4. P ， Q$ 为数轴上两点，点 $Р$ 从点 $A$ 出发以每秒 $1$ 个单位长度的速度向左运动，同时点 $Q$ 从点 $B$ 出发以每秒 $2$ 个单位长度的速度向左运动，点 $Q$ 到达原点 $О$ 后，立即以原来的速度返回，当点 $Q$ 回到点 $B$ 时，点 $Р$ 与点 $Q$ 同时停止运动．设点 $Р$ 运动的时间为 $x$ 秒，点 $Р$ 与点 $Q$ 之间的距离为 $y$ 个单位长度，则下列图像中表示 $y$ 与 $x$ 的函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题（每题3分，共18分）

11. 如图是A，B两种手机套餐每月资费y(元)与通话时间x(分钟)对应的函数图象，若小红每月通话时间大约为500分钟，则从A，B两种手机资费套餐中选择套餐更合适．

查看试题解析
12. 某长途汽车客运公司规定旅客可免费携带一定质量的行李.当行李的质量超过规定时，需付的行李费y（元）与行李质量 $x (kg)$ 之间满足一次函数关系，部分对应值如下表：

$x (kg)$

…

30

40

50

…

y（元）

…

4

6

8

…

则旅客最多可免费携带行李的质量是kg.

查看试题解析
13. 如图，已知直线l₁：y＝3x+1和直线l₁：y＝mx+n交于点P（1，b），则关于x，y的二元一次方程组 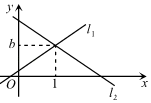${\begin{matrix} y = m x + n \\ y = 3 x + 1 \end{matrix}$ 的解是 .

查看试题解析
14. 已知直线y=x+b和y=ax+2交于点P（3，-1），则关于x的方程（a-1）x=b-2的解为．

查看试题解析
15. 如图，一次函数y＝kx+b的图象与x轴交于点A（3，0），与y轴交于点B（0，4），与正比例函数y＝ax的图象交于点C，且点C的横坐标为2，则不等式ax＜kx+b的解集为．

查看试题解析
16. 如图，在平面直角坐标系中，直线 $AB ： y = - x + b$ 交 $y$ 轴于点 $A (0 ， 2)$ ，交 $x$ 轴于点 $B$ ，直线1垂直平分 $OB$ 交 $AB$ 于点 $D$ ，交 $x$ 轴于点 $E$ ，点 $P$ 是直线1上且在第一象限一动点．若 $△ AOP$ 是等腰三角形，点 $P$ 的坐标是．

查看试题解析

三、解答题（共10题，共72分）

17. 医药研究所试验某种新药效时，成人如果按剂量服用，血液中每毫升含药量y（毫克）随时间x的变化如图所示，如果每毫升血液中含药量超过4微克（含4微克）时治疗疾病为有效，那么有效时间是多少小时？

查看试题解析
18. 如图，在靠墙（墙长为18m）的地方围建一个矩形的养鸡场，另三边用竹篱笆围成，如果竹篱笆总长为35m，求鸡场的长y （m）与宽x （m）的函数关系式，并求自变量的取值范围.

查看试题解析
19. 某水产养殖户有20吨水产品待售，现有两种销售方式：一是批发，二是零售．经过市场调查，这两种销售方式每天的销量及每吨所获的利润如下表：
销售方式
每天销量/吨
每吨所获利润/元
批发
3
4000
零售
1
6000
假设该养殖户售完20吨水产品，其中批发了x吨，所获总利润为y元．

(1)、求y与x之间的函数解析式；

(2)、因为人手紧缺，这个养殖户每天只能采用一种销售方式销售，且正好10天销售完所有水产品，请计算该养殖户所获总利润．

查看试题解析
20. 随着春节临近，某儿童游乐场推出了甲、乙两种消费卡，其中，甲为按照次数收费，乙为收取办卡费用以后每次打折收费．设消费次数为x时，所需费用为y元，且y与x的函数关系如图所示．根据图中信息，解答下列问题．

(1)、分别求出选择这两种卡消费时，y关于x的函数表达式；

(2)、求出入园多少次时，两者花费一样？费用是多少？

(3)、洋洋爸准备了240元，请问选择哪种划算？

查看试题解析
21. 如图1．函数 $y = \frac{1}{2} x + 3$ 与x轴交于点A，与y轴交于点B，点C与点A关于y轴对称．

(1)、①直接写出点C的坐标；
②求直线BC的函数解析式；

(2)、设点M是x轴上的一个动点，过点M作y轴的平行线，交直线AB于点P，交直线BC于点Q．连接BM，如图2，在点M的运动过程中是否存在点P，使∠BMP=∠BAC，若存在，请求出点P坐标；若不存在，请说明理由．

查看试题解析
22. 为了改善我市小区居位环境，构建“精美金华”，市政府持续对老旧小区进行改造，现要将200吨水泥，120吨外墙涂料运往某小区，计划租用甲、乙两种货车共8辆将这批水泥和外墙涂料全部运出，已知一辆甲种货车可装水泥和外墙涂料各20吨，一辆乙种货车可装水泥40吨和外墙涂料10吨．

(1)、请你设计方案安排甲、乙两种货车可一次性将货物运到目的地，有哪几种方案？

(2)、若甲种货车每辆要付运输费960元，乙种货车每辆要付运输费1200元，则应选择哪种方案使运输费最少？最少运费是多少？

查看试题解析
23. 我省要按照城市功能特点，城区消费到2022年，建设20个省内特色消费中心，着力发展“夜经济”，打造郑州“夜商都”等地方夜消费品牌升级版．允许市场经营主体在规范有序的条件下，采取“店铺外摆”“露天市场”方式进行销售．个体业主小王响应号召，采取“店铺外摆”方式销售甲、乙两款特价商品，两款商品的进价与售价如表所示：

甲商品

乙商品

进价（元/件）

35

5

售价（元/件）

45

8

小王计划购进甲、乙两种商品共100件进行销售．设小王购进甲商品 $x$ 件，甲、乙商品全部销售完后获得的利润为 $y$ 元．

(1)、求出 $y$ 与 $x$ 之间的函数关系式；

(2)、若购进乙商品的件数不少于甲商品件数的3倍，当购进甲，乙两种商品各多少件时，可使得甲、乙商品全部销售完后获得的利润最大？

查看试题解析
24. 某校八年级举行英语演讲比赛，购买A，B两种笔记本作为奖品，这两种笔记本的单价分别是12元和8元．根据比赛设奖情况，需购买笔记本共30本．

(1)、设买A笔记本n本，买两种笔记本的总费为w元，写出w（元）关于n（本）的函数关系式；

(2)、若所购买A笔记本的数量要不多于B笔记本数量的 $\frac{4}{5}$ ，但又不少于B笔记本数量的 $\frac{1}{5}$ ，购买这两种笔记本各多少时，费用最少？最少的费用是多少元？

(3)、若学校根据实际除了A，B两种笔记本外，还需一种单价为10元的C笔记本，若购买的总本数不变，C笔记本的数量是B笔记本的数量的2倍，A笔记本的数量不少于B笔记本的数量，试设计一种符合上述条件购买方案，且使所需费用最少．

查看试题解析
25. 目前，全国各地都在积极开展新冠肺炎疫苗接种工作，某生物公司接到批量生产疫苗任务，要求5天内加工完成22万支疫苗，该公司安排甲，乙两车间共同完成加工任务，乙车间加工过程中停工一段时间维修设备，然后提高效率继续加工，直到与甲车间同时完成加工任务为止，设甲，乙两车间各白生产疫苗y（万支）与甲车间加工时间x（天）之间的关系如图1所示；两车间未生产疫苗W（万支）与甲车间加工时间x（天）之间的关系如图2所示，请结合图象回答下列问题：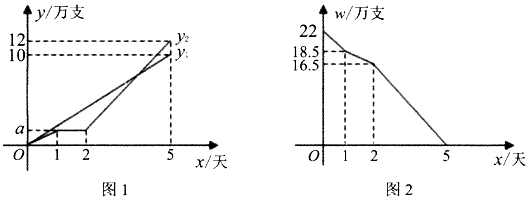

(1)、甲车间每天生产疫苗万支，第一天甲、乙两车间共生产疫苗万支，a＝；

(2)、当x＝3时，求甲、乙车间生产的疫苗数（万支）之差y₁﹣y₂；

(3)、若5.5万支疫苗恰好装满一辆货车，那么加工多长时间装满第一辆货车？再加工多长时间恰好装满第三辆货车？

查看试题解析
26. 某工厂投资组建了日废水处理量为20吨的废水处理车间，已知该车间处理废水时每天需固定成本30元，并且每处理一吨废水还需费用8元.若该车间在无法完成当天工业废水的处理任务时，需将超出20吨的部分交给第三方企业处理。如图所示为该厂日废水处理总费用y(元)与该厂日产生的工业废水x(吨)之间的函数关系图象.

(1)、求y关于x的函数关系式：

(2)、设该厂日废水处理的平均费用为a元/吨，
①当a=10时，在图1中画出直线y=ax的图象，结合图象判断直线y=ax与日废水处理总费用y的函数图象交点个数，求交点横坐标x的值并说明它的实际意义；

②当a=t时，参照上一小题的解法，求出该厂这日产生工业废水量x的值.

查看试题解析

销售方式	每天销量/吨	每吨所获利润/元
批发	3	4000
零售	1	6000

	甲商品	乙商品
进价（元/件）	35	5
售价（元/件）	45	8

t（min）	……	0	1	2	3	……
h（cm）	……	0.7	1.2	1.5	1.9	……

$x (kg)$	…	30	40	50	…
y（元）	…	4	6	8	…

2022-2023学年浙教版数学八上期末复习专题 一次函数的应用

一、单选题（每题2分，共20分）

二、填空题（每题3分，共18分）

三、解答题（共10题，共72分）

2022-2023学年浙教版数学八上期末复习专题一次函数的应用