2022-2023学年浙教版数学八上期末复习专题 一次函数的图象与性质
试卷更新日期:2022-11-19 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 下列各点在一次函数的图象上的是( )A、 B、 C、 D、2. 已知实数m<1,则一次函数y=(m﹣1)x+3﹣m图象经过的象限是( )A、一、二、三 B、二、三、四 C、一、三、四 D、一、二、四3. 把直线y=3x向下平移2个单位,得到的直线是( )A、y=3x﹣2 B、y=3(x﹣2) C、y=3x+2 D、y=3(x+2)4. 一次函数 与正比例函数 (m,n为常数、且 )在同一平面直角坐标系中的图可能是( )A、
 B、
B、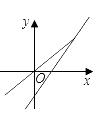 C、
C、 D、
D、 5. 一次函数的图象与轴交于点 , 将一次函数图象绕着点转动,转动后得到的一次函数图象与两坐标轴所围成的面积比原来增加2,则转动后得到的一次函数图象与轴交点横坐标为( )A、-3 B、3 C、3或-3 D、6或-66. 已知点在一次函数的图象上,则的大小关系是( )A、 B、 C、 D、不能确定7. 关于函数y=-2x+1,下列结论正确的是( )A、图象经过点 B、y随x的增大而增大 C、图象不经过第四象限 D、图象与直线y=-2x平行8. 一次函数y=-3x+2的图像经过( )A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限9. 点 ,点 是一次函数 图象上的两个点,且 ,则 为( )A、非正数 B、正数 C、负数 D、正数或负数10. 直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(﹣3,0),且两直线与y轴围成的三角形面积为12那么b2﹣b1的值为( )A、3 B、8 C、﹣6 D、﹣8
5. 一次函数的图象与轴交于点 , 将一次函数图象绕着点转动,转动后得到的一次函数图象与两坐标轴所围成的面积比原来增加2,则转动后得到的一次函数图象与轴交点横坐标为( )A、-3 B、3 C、3或-3 D、6或-66. 已知点在一次函数的图象上,则的大小关系是( )A、 B、 C、 D、不能确定7. 关于函数y=-2x+1,下列结论正确的是( )A、图象经过点 B、y随x的增大而增大 C、图象不经过第四象限 D、图象与直线y=-2x平行8. 一次函数y=-3x+2的图像经过( )A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限9. 点 ,点 是一次函数 图象上的两个点,且 ,则 为( )A、非正数 B、正数 C、负数 D、正数或负数10. 直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(﹣3,0),且两直线与y轴围成的三角形面积为12那么b2﹣b1的值为( )A、3 B、8 C、﹣6 D、﹣8二、填空题(每题3分,共18分)
-
11. 已知变量y与x满足一次函数关系,且y随x的变化而变化,若其图象经过第一、二、三象限,请写出一个满足上述要求的函数关系式.12. 一次函数y=(k+5)x﹣2中y随x的增大而减小,则k的取值范围是.13. 已知点P在直线上,且点P到y轴的距离为1,则点P的坐标为 .14. 如图,直线l1:y=x+1与x轴交于点A,与直线l2:y= x+2交于点B,点C为x轴上的一点,若△ABC为直角三角形,则点C的横坐标为 .
 15. 在平面直角坐标系中,若将一次函数y=2x+m-1的图象向右平移3个单位后,得到一个正比例函数的图象,则m的值为 .16. 如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,将沿过点A的直线折叠,使点B落在x轴的负半轴上,记作点C,折痕与y轴交于点D,则点D的坐标为 .
15. 在平面直角坐标系中,若将一次函数y=2x+m-1的图象向右平移3个单位后,得到一个正比例函数的图象,则m的值为 .16. 如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,将沿过点A的直线折叠,使点B落在x轴的负半轴上,记作点C,折痕与y轴交于点D,则点D的坐标为 .
三、解答题(共10题,共72分)
-
17. 大家在学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.学有所用:在等腰三角形ABC中,AB=AC , 其一腰上的高为h , M是底边BC上的任意一点,M到腰AB、AC的距离分别为h1、h2 .
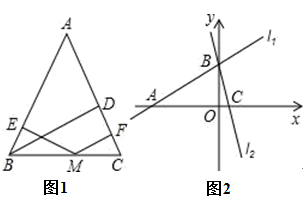 (1)、请你结合图1来证明:h1+h2=h;(2)、当点M在BC延长线上时,h1、h2、h之间又有什么样的结论.请你直接写出结论不必证明;(3)、利用以上结论解答,如图2在平面直角坐标系中有两条直线l1:y= x+3,l2:y=﹣3x+3,若l2上的一点M到l1的距离是 .求点M的坐标.18. 如图,已知直线y=﹣x+4与y轴交于点A,与x轴交于点B,过点C(1,0)作CD⊥x轴交直线AB于点D.点P是x轴上的一个动点,点E是BD的中点,在△PEF中(三顶点顺时针排列),∠PEF=90°,PE=EF.
(1)、请你结合图1来证明:h1+h2=h;(2)、当点M在BC延长线上时,h1、h2、h之间又有什么样的结论.请你直接写出结论不必证明;(3)、利用以上结论解答,如图2在平面直角坐标系中有两条直线l1:y= x+3,l2:y=﹣3x+3,若l2上的一点M到l1的距离是 .求点M的坐标.18. 如图,已知直线y=﹣x+4与y轴交于点A,与x轴交于点B,过点C(1,0)作CD⊥x轴交直线AB于点D.点P是x轴上的一个动点,点E是BD的中点,在△PEF中(三顶点顺时针排列),∠PEF=90°,PE=EF. (1)、则A、B、D三点的坐标分别为:A , B , D.(2)、如图,当点P在线段CB上时,若CP=2BP,求点F的坐标.(3)、当点P在射线CB上运动,连接AF.若S△AEF=5S△PBE , 求点P的坐标.19. 如图,在平面直角坐标系中,直线l1:y x+1交y轴于点A,直线l2:y x+t分别交y轴,x轴,直线l1于点B,C,D.
(1)、则A、B、D三点的坐标分别为:A , B , D.(2)、如图,当点P在线段CB上时,若CP=2BP,求点F的坐标.(3)、当点P在射线CB上运动,连接AF.若S△AEF=5S△PBE , 求点P的坐标.19. 如图,在平面直角坐标系中,直线l1:y x+1交y轴于点A,直线l2:y x+t分别交y轴,x轴,直线l1于点B,C,D. (1)、求点A的坐标,并用含t的代数式表示B,C,D的坐标;(2)、当t>0时,若S△OBC=S△OBD , 求t的值;(3)、P是x轴上的一点,连结AP,DP,若AP=DP,且∠APD=90°,求t的值.
(1)、求点A的坐标,并用含t的代数式表示B,C,D的坐标;(2)、当t>0时,若S△OBC=S△OBD , 求t的值;(3)、P是x轴上的一点,连结AP,DP,若AP=DP,且∠APD=90°,求t的值.