2022-2023学年浙教版数学八上期末复习专题图形与坐标

试卷更新日期：2022-11-19 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 根据下列表述，能够确定位置的是（）

A、甲地在乙地的正东方向上 B、一只风筝飞到距A处20米处 C、某市位于北纬30°，东经120° D、影院座位位于一楼二排

查看试题解析
2. 如果把电影票上3排6座记作（3，6），那么（6，5）表示（）

A、5排6座 B、5排5座 C、6排5座 D、6排6座

查看试题解析
3. 2021年9月15日，中华人民共和国第十四届运动会开幕式在西安奥体中心举行，如图，如果将西安钟楼的位置记为直角坐标系的原点，下列哪个点的位置可以表示奥体中心的位置（）

A、(－2，3) B、(2，3) C、(－2，－3) D、(2，－3)

查看试题解析

4. 如图是北京市地图简图的一部分，图中“故宫”、“颐和园”所在的区域分别是（）

	D	E	F
6	颐和园	奥运村
7		故宫	日坛
8		天坛

A、D7，E6 B、D6，E7 C、E7，D6 D、E6，D7

查看试题解析

5. 已知点 $A$ 的坐标为 $(a + 1 ， 3 - a)$ ，下列说法正确的是（）

A、若点 $A$ 在 $y$ 轴上，则 $a = 3$ B、若点 $A$ 在一三象限角平分线上，则 $a = 1$ C、若点 $A$ 到 $x$ 轴的距离是3 ，则 $a = \pm 6$ D、若点 $A$ 在第四象限，则 $a$ 的值可以为-2

查看试题解析
6. 如图是一只蝴蝶标本，已知表示蝴蝶两“翅膀尾部”A，B 两点的坐标分别为（－2，－3），（2，－3），则表示蝴蝶身体“尾部”C 点的坐标为（）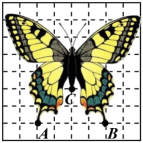

A、（0，－1） B、（1，－1） C、（－1，0） D、（2，－1）

查看试题解析
7. 若点 $P (2 - m ， 5)$ 在y轴上，则m的值等于（　　）

A、 $2$ B、 $7$ C、 $- 2$ D、 $- 3$

查看试题解析
8. 已知图形A全部在x轴的上方，如果将图形A上的所有点的纵坐标都乘以－1，横坐标不变得到图形B，则（）

A、两个图形关于x轴对称 B、两个图形关于y轴对称 C、两个图形重合 D、两个图形不关于任何一条直线对称

查看试题解析
9. 点 $A (2 ， m)$ 向上平移2个单位后与点 $B (n ， - 1)$ 关于y轴对称，则 $m^{n} =$ （）.

A、1 B、 $\frac{1}{2}$ C、 $- \frac{1}{8}$ D、 $\frac{1}{9}$

查看试题解析
10. 在平面直角坐标系中，将点A(a，1-a)先向左平移3个单位得点A₁ ，再将A₁向上平移1个单位得点A₂ ，若点A₂落在第三象限，则a的取值范围是（）

A、2 $< a <$ 3 B、a $<$ 3 C、a $>$ 2 D、a $<$ 2或a $>$ 3

查看试题解析

二、填空题（每题4分，共24分）

11. 如图是一台雷达探测相关目标得到的结果，若记图中目标A的位置为(2， $90 °$ )，目标B 的位置为(4， $30 °$ )，现有一个目标C的位置为(3， $m °$ )，且与目标B的距离为5，则目标C的位置为．

查看试题解析
12. 已知点 $M (2 m - 1 ， - 3)$ ，点 $N (5 ， 2)$ ，直线 $M N ∥ y$ 轴，则m的值为．

查看试题解析
13. 点 $A (m - 1 ， 2 m - 3)$ 在第一、三象限夹角的角平分线上，则m的值为．

查看试题解析
14. 点 $P (a ， - 3)$ 与 $Q (2 ， b)$ 关于y轴对称，则 $a^{b}$ 的值为．

查看试题解析
15. 如图，已知A₁（0，1），A₂（ $\frac{\sqrt{3}}{2}$ ， $- \frac{1}{2}$ ），A₃（ $- \frac{\sqrt{3}}{2}$ ， $- \frac{1}{2}$ ），A₄（0，2），A₅（ $\sqrt{3}$ ，-1），A₆（ $- \sqrt{3}$ ，-1），A₇（0，3），A₈（ $\frac{3 \sqrt{3}}{2}$ ， $- \frac{3}{2}$ ），A₉（ $- \frac{3 \sqrt{3}}{2}$ ， $- \frac{3}{2}$ ）……则点A₂₀₁₀的坐标是

查看试题解析
16. 若 $(x + 2) (x - 3) = x^{2} + b x + c$ ，其中b，c为常数，则点P（b，c）关于x轴的对称点的坐标为．

查看试题解析

三、解答题（共8题，共66分）

17. 小明和朋友到人民公园游玩，回到家后，利用平面直角坐标系画出了公园的景区地图，如图所示．可是他忘记了在图中标出原点和x轴、y轴，只知道游乐园D的坐标为(1，﹣3)，请你帮他画出平面直角坐标系，并写出其他各景点的坐标．

查看试题解析
18. 已知点A（m﹣2，5）和B（3，n＋4），A ， B两点关于y轴对称，求m﹣n的值．

查看试题解析
19. 如图，利用关于坐标轴对称的点的坐标的特点，画出与 $△ A B C$ 关于x轴对称的图形．

查看试题解析
20. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（-4，5），（-1，3）．

⑴请在如图所示的网格平面内作出平面直角坐标系；

⑵请作出△ABC关于y轴对称的△A′B′C′；

⑶写出点B′的坐标．

查看试题解析
21. 已知点 $P (3 a - 15 ， 2 - a)$ ．

(1)、若点 $P$ 位于第四象限，它到 $x$ 轴的距离是4 ，试求出 $a$ 的值：

(2)、若点 $P$ 位于第三象限且横、纵坐标都是整数，试求点 $P$ 的坐标．

查看试题解析
22. 如图，平面直角坐标系中，A（﹣2，1），B（﹣3，4），C（﹣1，3），过点（1，0）作x轴的垂线l．

(1)、作出△ABC关于直线l的轴对称图形 $△ A_{1} B_{1} C_{1}$ ；

(2)、直接写出 $A_{1}$ （，）， $B_{1}$ （，）， $C_{1}$ （，）；

(3)、在△ABC内有一点P（m，n），则点P关于直线l的对称点 $P_{1}$ 的坐标为（，）（结果用含m，n的式子表示）．

查看试题解析
23. 如图回答下列问题：

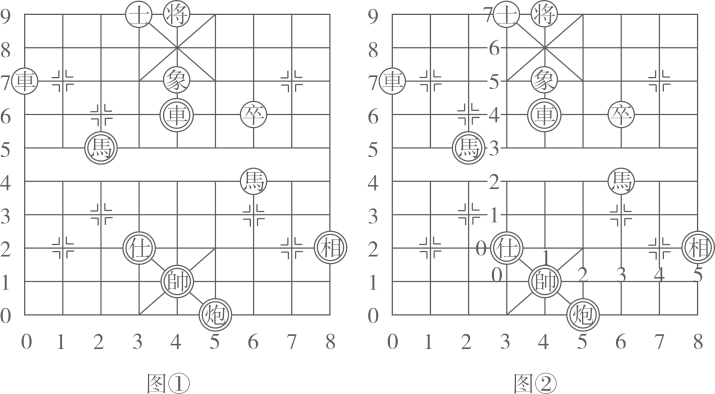(1)、如图①所示，请用有序数对写出棋盘上棋子“帅、黑车、炮”的位置（把列号写在前面，行号写在后面）．

(2)、如图②所示把O点移动到棋子“仕”的位置时，用有序数对写出棋子“仕、相、黑马”的位置（把列号写在前面，行号写在后面）

(3)、如图②，已知棋子“将”的位置是（2，8），棋子“黑马”的位置是（4，3），规定列在前，行在后，请你在棋盘上确定A（0，0）点的位置，棋子“红马”的位置是什么？

查看试题解析
24. 在如图的正方形网格中，每一个小正方形的边长为1，格点三角形ABC（顶点是网格线交点的三角形）的三个顶点的坐标分别为 $A (1 ， 1)$ ， $B (4 ， 2)$ ， $C (3 ， 4)$

(1)、请在图中的网格平面内建立平面直角坐标系，并将 $△ A B C$ 画出来．

(2)、在图中找一点D，使 $A D = \sqrt{26}$ ， $C D = \sqrt{13}$ ，并将点D标记出来．

(3)、在x轴上找一点P，使 $P A + P B$ 的值最小，请直接写出点P的坐标．

(4)、在y轴上是否存在点Q，使得 $S_{△ A O Q} = \frac{1}{2} S_{△ A B C}$ ，如果存在，求出点Q的坐标，如果不存在，说明理由．

查看试题解析

2022-2023学年浙教版数学八上期末复习专题 图形与坐标

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2022-2023学年浙教版数学八上期末复习专题图形与坐标