2022-2023学年浙教版数学九上期末复习专题 简单几何体的表面展开图
试卷更新日期:2022-11-19 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 下列图形中,为圆柱的侧面展开图的是( )A、
 B、
B、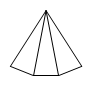 C、
C、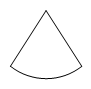 D、
D、 2. 如图为一个几何体的表面展开图,则该几何体是( )
2. 如图为一个几何体的表面展开图,则该几何体是( )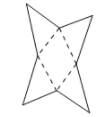 A、三棱锥 B、四棱锥 C、四棱柱 D、圆锥3. 下列图形中经过折叠,可以围成圆锥的是( )A、
A、三棱锥 B、四棱锥 C、四棱柱 D、圆锥3. 下列图形中经过折叠,可以围成圆锥的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
4. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( ) A、
A、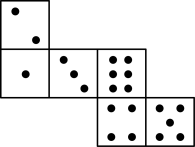 B、
B、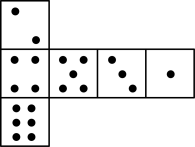 C、
C、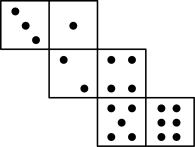 D、
D、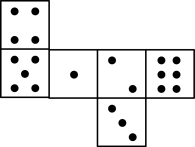 5. 如图是正方体的表面展开图,每个面内都分别写有一个字,则与“创”字相对面上的字是( )
5. 如图是正方体的表面展开图,每个面内都分别写有一个字,则与“创”字相对面上的字是( )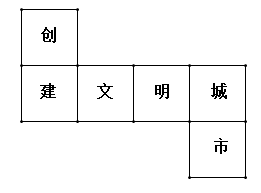 A、文 B、明 C、城 D、市6. 一个正方体的相对的表面上所标的数都是互为相反数的两个数,如图是这个正方体的表面展开图,那么图中x的值是( )
A、文 B、明 C、城 D、市6. 一个正方体的相对的表面上所标的数都是互为相反数的两个数,如图是这个正方体的表面展开图,那么图中x的值是( ) A、-8 B、-3 C、-2 D、37. 下图所示的长方形(长为14,宽为8)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( )
A、-8 B、-3 C、-2 D、37. 下图所示的长方形(长为14,宽为8)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( ) A、56 B、40 C、28 D、208. 如图(1)是一个小正方体的表面展开图,小正方体从图(2)所示位置依次翻转到第①格、第②格,第③格,第④格,这时小正方体朝上一面的字是( )
A、56 B、40 C、28 D、208. 如图(1)是一个小正方体的表面展开图,小正方体从图(2)所示位置依次翻转到第①格、第②格,第③格,第④格,这时小正方体朝上一面的字是( ) A、六 B、中 C、学 D、强9. 如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:mm).电镀时,如果每平方米用锌0.1千克,电镀1000个这样的锚标浮筒,需要多少千克锌?(π的值取3.14)( )
A、六 B、中 C、学 D、强9. 如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:mm).电镀时,如果每平方米用锌0.1千克,电镀1000个这样的锚标浮筒,需要多少千克锌?(π的值取3.14)( )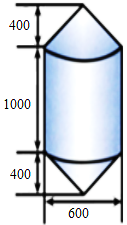 A、282.6 B、282600000 C、357.96 D、35796000010. 一个圆柱体和一个圆锥体的底面周长之比是 ,它们的体积比也是 ,圆柱和圆锥的高的比是( )A、1:1 B、3:1 C、1:9 D、1:3
A、282.6 B、282600000 C、357.96 D、35796000010. 一个圆柱体和一个圆锥体的底面周长之比是 ,它们的体积比也是 ,圆柱和圆锥的高的比是( )A、1:1 B、3:1 C、1:9 D、1:3二、填空题(每题4分,共24分)
-
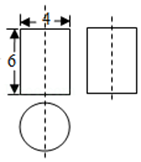
11. 如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是(结果保留π).
 12. 如图,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,所得几何体的体积为cm3.(结果保留π)
12. 如图,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,所得几何体的体积为cm3.(结果保留π) 13. 如图,圆锥的母线长 , 底面圆的周长是 , 则圆锥的侧面积是 .
13. 如图,圆锥的母线长 , 底面圆的周长是 , 则圆锥的侧面积是 . 14. 若一个圆锥体的底面积是其表面积的 , 则其侧面展开图圆心角的度数为 .15. 把一个正方体纸盒展成一个平面图形,至少需要剪开条棱.16. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).
14. 若一个圆锥体的底面积是其表面积的 , 则其侧面展开图圆心角的度数为 .15. 把一个正方体纸盒展成一个平面图形,至少需要剪开条棱.16. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).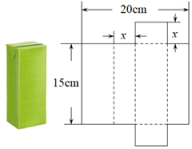
三、解答题(共8题,共66分)
-
17. 将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.(1)、以下两个方格图中的阴影部分能表示立方体表面展开图的是(填A或B).
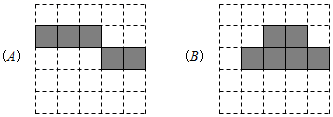 (2)、在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示)
(2)、在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示) (3)、如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)
(3)、如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)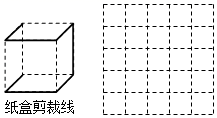
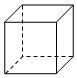 18. 如图,已知圆柱底面的直径 ,圆柱的高 ,在圆柱的侧面上,过点 , 嵌有一圈长度最短的金属丝.(1)、现将圆柱侧面沿 剪开,所得的圆柱侧面展开图是______.A、
18. 如图,已知圆柱底面的直径 ,圆柱的高 ,在圆柱的侧面上,过点 , 嵌有一圈长度最短的金属丝.(1)、现将圆柱侧面沿 剪开,所得的圆柱侧面展开图是______.A、 ;
B、
;
B、 ;
C、
;
C、 ;
D、
;
D、 (2)、求该长度最短的金属丝的长.
(2)、求该长度最短的金属丝的长. 19. 如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
19. 如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π) 20. “赶陀螺”是一项深受人们喜爱的民族性运动,如图所示是一个陀螺的立体结构图.已知底面圆的直径 ,圆柱体部分的高 ,圆锥体部分的高 ,求出这个陀螺的表面积(结果保留 ).
20. “赶陀螺”是一项深受人们喜爱的民族性运动,如图所示是一个陀螺的立体结构图.已知底面圆的直径 ,圆柱体部分的高 ,圆锥体部分的高 ,求出这个陀螺的表面积(结果保留 ).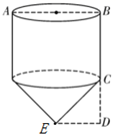 21. 有一个顶部是圆锥,底部是圆柱的粮囤模型,如图是它的主视图.
21. 有一个顶部是圆锥,底部是圆柱的粮囤模型,如图是它的主视图.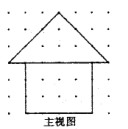 (1)、画出该粮囤模型的俯视图;(2)、若每相邻两个格点之间的距离均表示1米,请计算:
(1)、画出该粮囤模型的俯视图;(2)、若每相邻两个格点之间的距离均表示1米,请计算:①在粮囤顶部铺上油毡,需要多少平方米油毡(油毡接缝重合部分不计)?
②若粮食最多只能装至与圆柱同样高,则最多可以存放多少立方米粮食?(结果保留 和根号)
22. 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作: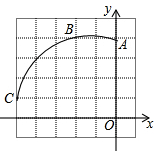 (1)、利用网格确定该圆弧所在圆的圆心D点的位置,并写出点D坐标为 ▲ ;(2)、连接AD、CD,则⊙D的半径为(结果保留根号),∠ADC的度数为;(3)、若扇形DAC是一个圆锥的侧面展开图,则该圆锥底面半径为 . (结果保留根号).23. 一块材料的形状是等腰△ABC,底边 BC=120 cm,高 AD=120 cm.
(1)、利用网格确定该圆弧所在圆的圆心D点的位置,并写出点D坐标为 ▲ ;(2)、连接AD、CD,则⊙D的半径为(结果保留根号),∠ADC的度数为;(3)、若扇形DAC是一个圆锥的侧面展开图,则该圆锥底面半径为 . (结果保留根号).23. 一块材料的形状是等腰△ABC,底边 BC=120 cm,高 AD=120 cm. (1)、若把这块材料加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在AB,AC 上(如图 1),则这个正方形的边长为多少?(2)、若把这块材料加工成正方体零件(如图 2,阴影部分为正方体展开图),则正方体的表面积为多少?24. 某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1.
(1)、若把这块材料加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在AB,AC 上(如图 1),则这个正方形的边长为多少?(2)、若把这块材料加工成正方体零件(如图 2,阴影部分为正方体展开图),则正方体的表面积为多少?24. 某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1. (1)、由三视图可知,密封纸盒的形状是;(2)、根据该几何体的三视图,在图2中补全它的表面展开图;(3)、请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)
(1)、由三视图可知,密封纸盒的形状是;(2)、根据该几何体的三视图,在图2中补全它的表面展开图;(3)、请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)