2022-2023学年浙教版数学九上期末复习专题 投影
试卷更新日期:2022-11-19 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 太阳发出的光照在物体上是 , 路灯发出的光照在物体上是 ( )A、平行投影,中心投影 B、中心投影,平行投影 C、平行投影,平行投影 D、中心投影,中心投影2. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图所示是滨河公园中的两个物体一天中四个不同时刻在太阳光的照射下落在地面上的影子,按照时间的先后顺序排列正确的是( )
3. 如图所示是滨河公园中的两个物体一天中四个不同时刻在太阳光的照射下落在地面上的影子,按照时间的先后顺序排列正确的是( ) A、(3)(4)(1)(2) B、(4)(3)(1)(2) C、(4)(3)(2)(1) D、(2)(4)(3)(1)4. 一个矩形木框在太阳光的照射下,在地面上的投影不可能是( )A、
A、(3)(4)(1)(2) B、(4)(3)(1)(2) C、(4)(3)(2)(1) D、(2)(4)(3)(1)4. 一个矩形木框在太阳光的照射下,在地面上的投影不可能是( )A、 B、
B、 C、
C、 D、
D、 5. 三根等长的木杆竖直地立在平地的同一个圆周上,圆心处有一盏灯光,其俯视图如图所示,图中画出了其中一根木杆在灯光下的影子.下列四幅图中正确画出另两根木杆在同一灯光下的影子的是( )
5. 三根等长的木杆竖直地立在平地的同一个圆周上,圆心处有一盏灯光,其俯视图如图所示,图中画出了其中一根木杆在灯光下的影子.下列四幅图中正确画出另两根木杆在同一灯光下的影子的是( ) A、
A、 B、
B、 C、
C、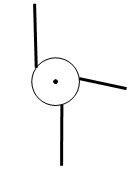 D、
D、 6. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )
6. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( ) A、
A、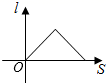 B、
B、 C、
C、 D、
D、 7. 如图,小颖身高为 ,在阳光下影长 ,当她走到距离墙角(点 ) 的 处时,她的部分影子投射到墙上,则投射在墙上的影子 的长度为( )
7. 如图,小颖身高为 ,在阳光下影长 ,当她走到距离墙角(点 ) 的 处时,她的部分影子投射到墙上,则投射在墙上的影子 的长度为( ) A、 B、 C、 D、8. 如图,电灯在横杆的正上方,在灯光下的影长为 , , , , 点到的距离是 , 则点到的距离是( )
A、 B、 C、 D、8. 如图,电灯在横杆的正上方,在灯光下的影长为 , , , , 点到的距离是 , 则点到的距离是( ) A、 B、 C、 D、9. 如图,一直角边长为4cm的等腰直角三角板在灯光照射下形成投影,该三角板与其投影的相似比为2∶3.则投影三角形的面积为( )
A、 B、 C、 D、9. 如图,一直角边长为4cm的等腰直角三角板在灯光照射下形成投影,该三角板与其投影的相似比为2∶3.则投影三角形的面积为( ) A、36 B、18 C、16 D、2010. 圆桌面(桌面中间有一个直径为1m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为2m,桌面离地面1m,若灯泡离地面2m,则地面圆环形阴影的面积是( )
A、36 B、18 C、16 D、2010. 圆桌面(桌面中间有一个直径为1m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为2m,桌面离地面1m,若灯泡离地面2m,则地面圆环形阴影的面积是( ) A、2πm2 B、3πm2 C、6πm2 D、12πm2
A、2πm2 B、3πm2 C、6πm2 D、12πm2二、填空题(每题4分,共24分)
-
11. 皮影戏是一种以兽皮或纸板做成的人物剪影,在灯光照射下用隔亮布进行表演的民间戏剧.表演者在幕后操纵剪影、演唱,或配以音乐,具有浓厚的乡土气息.“皮影戏”中的皮影是(填写“平行投影”或“中心投影”)
 12. 一块直角三角板如图所示放置, , , , 测得边在平面的中心投影长为 , 则长为 , 的面积是 .
12. 一块直角三角板如图所示放置, , , , 测得边在平面的中心投影长为 , 则长为 , 的面积是 . 13. 如图,小树AB在路灯O的照射下形成树影BC. 若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=5m,则路灯的高度OP为 m.
13. 如图,小树AB在路灯O的照射下形成树影BC. 若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=5m,则路灯的高度OP为 m. 14. 小亮的身高1.8m,他在阳光下的影长为0.6m;同一时刻,学校的旗杆影长为3m,则该旗杆的高度是 .15. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ 的长度为m.
14. 小亮的身高1.8m,他在阳光下的影长为0.6m;同一时刻,学校的旗杆影长为3m,则该旗杆的高度是 .15. 在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ 的长度为m.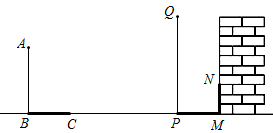 16. 莆田湄洲岛,是亿万妈祖信徒敬仰的圣地,这里的妈祖庙更是名扬四海.在湄洲妈祖庙的正殿前方上建造了一尊巨型石雕妈祖像,面向台湾海峡,为海峡两岸同胞共同瞻仰.小颖想测量雕像的高,她先测得雕像的影长为 ,并在同一时刻测得一根长为 的竹竿的影长是 .请你帮她算一下,石雕妈祖像高是m.
16. 莆田湄洲岛,是亿万妈祖信徒敬仰的圣地,这里的妈祖庙更是名扬四海.在湄洲妈祖庙的正殿前方上建造了一尊巨型石雕妈祖像,面向台湾海峡,为海峡两岸同胞共同瞻仰.小颖想测量雕像的高,她先测得雕像的影长为 ,并在同一时刻测得一根长为 的竹竿的影长是 .请你帮她算一下,石雕妈祖像高是m.
三、解答题(共8题,共66分)
-
17. 如图,两幅图片中竹竿的影子是在太阳光下形成的,还是在灯光下形成的?请你画出两图中小树的影子.
 18. 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.
18. 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.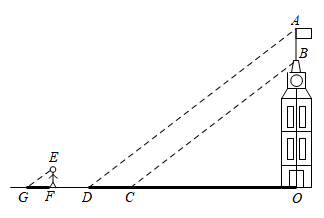 19. 据说,在距今2500多年前,古希腊数学家就已经较准确地测出了埃及金字塔的高度,操作过程大致如下:如图所示,设AB是金字塔的高,在某一时刻,阳光照射下的金字塔在底面上投下了一个清晰的阴影,塔顶A的影子落在地面上的点C处,金字塔底部可看作方正形FGHI,测得正方形边长FG长为160米,点B在正方形的中心,BC与金字塔底部一边垂直于点K,与此同时,直立地面上的一根标杆DO留下的影子是OE,射向地面的太阳光线可看作平行线(AC∥DE),此时测得标杆DO长为1.2米,影子OE长为2.7米,KC长为250米,求金字塔的高度AB及斜坡AK的坡度(结果均保留四个有效数字)
19. 据说,在距今2500多年前,古希腊数学家就已经较准确地测出了埃及金字塔的高度,操作过程大致如下:如图所示,设AB是金字塔的高,在某一时刻,阳光照射下的金字塔在底面上投下了一个清晰的阴影,塔顶A的影子落在地面上的点C处,金字塔底部可看作方正形FGHI,测得正方形边长FG长为160米,点B在正方形的中心,BC与金字塔底部一边垂直于点K,与此同时,直立地面上的一根标杆DO留下的影子是OE,射向地面的太阳光线可看作平行线(AC∥DE),此时测得标杆DO长为1.2米,影子OE长为2.7米,KC长为250米,求金字塔的高度AB及斜坡AK的坡度(结果均保留四个有效数字) 20. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,求路灯的高.
20. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,求路灯的高.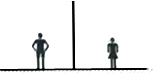 21. 如图,一路灯与墙相距20米,当身高米的小亮在离墙17米的D处时,影长为1米.
21. 如图,一路灯与墙相距20米,当身高米的小亮在离墙17米的D处时,影长为1米. (1)、求路灯B的高度;(2)、若点P为路灯,请画出小亮位于N处时,在路灯P下的影子NF(用粗线段表示出来)22. 阅读以下文字并解答问题:在“物体的高度”活动中,某数学兴趣小组的4名同学选择了测量学校里的四棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
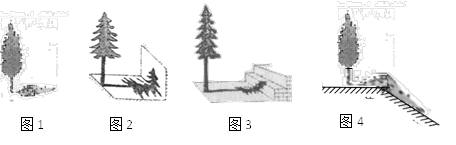
(1)、求路灯B的高度;(2)、若点P为路灯,请画出小亮位于N处时,在路灯P下的影子NF(用粗线段表示出来)22. 阅读以下文字并解答问题:在“物体的高度”活动中,某数学兴趣小组的4名同学选择了测量学校里的四棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:小芳:测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4.08米(如图1).
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图2),墙壁上的影长为1.2米,落在地面上的影长为2.4米.
小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图3),测得此影子长为0.2米,一级台阶高为0.3米,落在地面上的影长为4.4米.
小明:测得丁树落在地面上的影长为2.4米,落在坡面上影长为3.2米(如图4).身高是1.6m的小明站在坡面上,影子也都落坡面上,小芳测得他的影长为2m.
 (1)、在横线上直接填写甲树的高度为米.(2)、求出乙树的高度(画出示意图).(3)、请选择丙树的高度为( )A、6.5米 B、5.75米 C、6.05米 D、7.25米(4)、你能计算出丁树的高度吗?试试看.23. 测量金字塔高度:如图1,金字塔是正四棱锥 ,点O是正方形 的中心 垂直于地面,是正四棱锥 的高,泰勒斯借助太阳光.测量金字塔影子 的相关数据,利用平行投影测算出了金字塔的高度,受此启发,人们对甲、乙、丙三个金字塔高度也进行了测量.甲、乙、丙三个金字塔都用图1的正四棱锥 表示.
(1)、在横线上直接填写甲树的高度为米.(2)、求出乙树的高度(画出示意图).(3)、请选择丙树的高度为( )A、6.5米 B、5.75米 C、6.05米 D、7.25米(4)、你能计算出丁树的高度吗?试试看.23. 测量金字塔高度:如图1,金字塔是正四棱锥 ,点O是正方形 的中心 垂直于地面,是正四棱锥 的高,泰勒斯借助太阳光.测量金字塔影子 的相关数据,利用平行投影测算出了金字塔的高度,受此启发,人们对甲、乙、丙三个金字塔高度也进行了测量.甲、乙、丙三个金字塔都用图1的正四棱锥 表示. (1)、测量甲金字塔高度:如图2,是甲金字塔的俯视图,测得底座正方形 的边长为 ,金字塔甲的影子是 ,此刻,1米的标杆影长为0.7米,则甲金字塔的高度为m.(2)、测量乙金字塔高度:如图1,乙金字塔底座正方形 边长为 ,金字塔乙的影子是 , ,此刻1米的标杆影长为0.8米,请利用已测出的数据,计算乙金字塔的高度.24. 小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:
(1)、测量甲金字塔高度:如图2,是甲金字塔的俯视图,测得底座正方形 的边长为 ,金字塔甲的影子是 ,此刻,1米的标杆影长为0.7米,则甲金字塔的高度为m.(2)、测量乙金字塔高度:如图1,乙金字塔底座正方形 边长为 ,金字塔乙的影子是 , ,此刻1米的标杆影长为0.8米,请利用已测出的数据,计算乙金字塔的高度.24. 小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答: (1)、如图1,白天在阳光下,小彬将木杆 水平放置,此时木杆在水平地面上的影子为线段 .
(1)、如图1,白天在阳光下,小彬将木杆 水平放置,此时木杆在水平地面上的影子为线段 .①若木杆 的长为 ,则其影子 的长为 ;
②在同一时刻同一地点,将另一根木杆 直立于地面,请画出表示此时木杆 在地面上影子的线段 ;
(2)、如图2,夜晚在路灯下,小彬将木杆 水平放置,此时木杆在水平地面上的影子为线段 .①请在图中画出表示路灯灯泡位置的点 ;
②若木杆 的长为 ,经测量木杆 距离地面 ,其影子 的长为 ,则路灯 距离地面的高度为 .