2022-2023学年浙教版数学九上期末复习专题 三角形的内切圆
试卷更新日期:2022-11-19 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 已知是的内切圆,且 , , 则等于( )
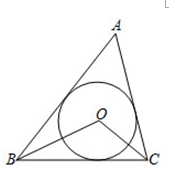 A、 B、 C、 D、2. 如图,△ABC中,∠C=90°,BC=5,⊙O与△ABC的三边相切于点D、E、F,若⊙O的半径为2,则△ABC的周长为( )
A、 B、 C、 D、2. 如图,△ABC中,∠C=90°,BC=5,⊙O与△ABC的三边相切于点D、E、F,若⊙O的半径为2,则△ABC的周长为( ) A、14 B、20 C、24 D、303. 如图,点I是的内心,若 , 则等于( )
A、14 B、20 C、24 D、303. 如图,点I是的内心,若 , 则等于( ) A、50° B、52° C、54° D、56°4. 如图,在中, , , , 则的内切圆半径r长为( )
A、50° B、52° C、54° D、56°4. 如图,在中, , , , 则的内切圆半径r长为( )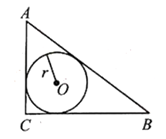 A、1.5 B、1 C、2 D、1.25. 已知的内心为P,则下列说法错误的是( )A、 B、P在的内部 C、P为三个内角平分线的交点 D、P到三边距离相等6. 如图,△ABC周长为20cm,BC=6cm,圆O是△ABC的内切圆,圆O的切线MN与AB、CA相交于点M、N,则△AMN的周长为( )
A、1.5 B、1 C、2 D、1.25. 已知的内心为P,则下列说法错误的是( )A、 B、P在的内部 C、P为三个内角平分线的交点 D、P到三边距离相等6. 如图,△ABC周长为20cm,BC=6cm,圆O是△ABC的内切圆,圆O的切线MN与AB、CA相交于点M、N,则△AMN的周长为( ) A、14cm B、8cm C、7cm D、9cm7. 如图,中, , , 点O是的内心.则等于( )
A、14cm B、8cm C、7cm D、9cm7. 如图,中, , , 点O是的内心.则等于( ) A、124° B、118° C、112° D、62°8. 如图,△ABC是一张周长为18cm的三角形纸片,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,若剪下的三角形的周长为8cm,则BC为( )
A、124° B、118° C、112° D、62°8. 如图,△ABC是一张周长为18cm的三角形纸片,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,若剪下的三角形的周长为8cm,则BC为( ) A、8cm B、5cm C、6.5cm D、无法确定9. 如图,△ABC中,∠C=90°,AC=12,BC=5,⊙O与△ABC的三边相切于点D、E、F,则AD长为( )
A、8cm B、5cm C、6.5cm D、无法确定9. 如图,△ABC中,∠C=90°,AC=12,BC=5,⊙O与△ABC的三边相切于点D、E、F,则AD长为( ) A、8 B、10 C、12 D、1410. 一直角三角形的斜边长为c,其内切圆半径是r,则三角形面积与其内切圆的面积之比是( )A、 B、 C、 D、
A、8 B、10 C、12 D、1410. 一直角三角形的斜边长为c,其内切圆半径是r,则三角形面积与其内切圆的面积之比是( )A、 B、 C、 D、二、填空题(每题4分,共24分)
-
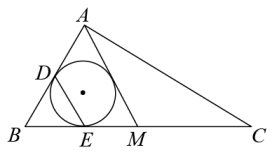
11. 已知一个三角形的三边长分别为5、7、8,则其内切的半径为 .12. 如图,中, , M是BC的中点,的内切圆与AB,BM分别相切于点D,E,连接DE.若 , 则的大小为 .
 13. 若方程x2-7x+12=0的两个根分别是直角三角形两直角边的长,则这个直角三角形的内切圆半径为.14. 如图,点I和O分别是△ABC的内心和外心,若∠AIB=125°,则∠AOB的度数为 .
13. 若方程x2-7x+12=0的两个根分别是直角三角形两直角边的长,则这个直角三角形的内切圆半径为.14. 如图,点I和O分别是△ABC的内心和外心,若∠AIB=125°,则∠AOB的度数为 . 15. 如图,在中, , 半径为3cm的是的内切圆,连接、 , 则图中阴影部分的面积是cm2.(结果用含的式子表示)
15. 如图,在中, , 半径为3cm的是的内切圆,连接、 , 则图中阴影部分的面积是cm2.(结果用含的式子表示)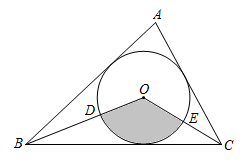 16. 《九章算术》是我国古代的数学名著,书中有这样的一个问题:“今有勾八步,股十五步,问勾中容圆径几何?”.其意思是:“如图,现有直角三角形,勾(短直角边)长为 8 步,股(长直角边)长为 15 步,问该直角三角形所能容纳的最大圆的直径是多少?”答:该直角三角形所能容纳的最大圆的直径是步.
16. 《九章算术》是我国古代的数学名著,书中有这样的一个问题:“今有勾八步,股十五步,问勾中容圆径几何?”.其意思是:“如图,现有直角三角形,勾(短直角边)长为 8 步,股(长直角边)长为 15 步,问该直角三角形所能容纳的最大圆的直径是多少?”答:该直角三角形所能容纳的最大圆的直径是步.
三、解答题(共8题,共66分)
-
17. 的顶点都在正方形网格格点上,如图所示.
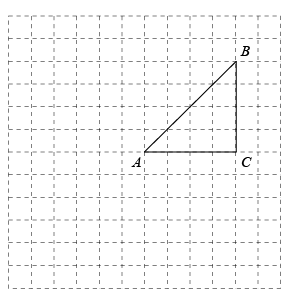 (1)、将绕点A顺时针方向旋转得到(点对应点), 画出 .(2)、请找出过三点的圆的圆心, 标明圆心的位置.18. 已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.
(1)、将绕点A顺时针方向旋转得到(点对应点), 画出 .(2)、请找出过三点的圆的圆心, 标明圆心的位置.18. 已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.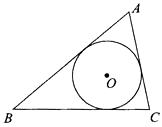 19. 已知:如图,点 是△ 的内心, 的延长线和△ 的外接圆相交于点 .求证: .
19. 已知:如图,点 是△ 的内心, 的延长线和△ 的外接圆相交于点 .求证: . 20. 已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°.
20. 已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°.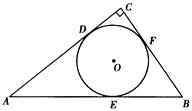 (1)、若AC=12cm,BC=9cm,求⊙O的半径r;
(1)、若AC=12cm,BC=9cm,求⊙O的半径r;
(2)、若AC=b,BC=a,AB=c,求⊙O的半径r.21. 图,在中,AB=AC,⊙O是的外接圆,点D在⊙O上且∠BCD=∠ACB,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF. (1)、求证:AF是⊙O的切线;(2)、若点G是的内心, , 求BG的长.22. 已知开口向上的抛物线 与直线:y=ax+c,y=cx+a中的每一条都至多有一个公共点.(1)、求 的最大值;(2)、当 取最大值时,设直线 交抛物线 于A,B两点,C为抛物线的顶点,若△ABC内切圆的半径为1,求a的值.23. 如图, 是△ABC的外心,I是△ABC的内心,连AI并延长交BC和⊙O于D、E两点.
(1)、求证:AF是⊙O的切线;(2)、若点G是的内心, , 求BG的长.22. 已知开口向上的抛物线 与直线:y=ax+c,y=cx+a中的每一条都至多有一个公共点.(1)、求 的最大值;(2)、当 取最大值时,设直线 交抛物线 于A,B两点,C为抛物线的顶点,若△ABC内切圆的半径为1,求a的值.23. 如图, 是△ABC的外心,I是△ABC的内心,连AI并延长交BC和⊙O于D、E两点. (1)、求证:EB=EI;(2)、若AB=4,AC=3,BE=2,求AI的长.24. 我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设 , , 为三角形三边, 为面积,则 ①
(1)、求证:EB=EI;(2)、若AB=4,AC=3,BE=2,求AI的长.24. 我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设 , , 为三角形三边, 为面积,则 ①这是中国古代数学的瑰宝之一.
而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设 (周长的一半),则 ②
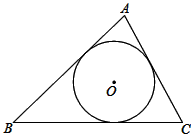 (1)、尝试验证.这两个公式在表面上形式很不一致,请你用以5,7,8为三边构成的三角形,分别验证它们的面积值;(2)、问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从① ②或者② ① ;(3)、问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图, 的内切圆半径为 ,三角形三边长为 , , ,仍记 , 为三角形面积,则 .
(1)、尝试验证.这两个公式在表面上形式很不一致,请你用以5,7,8为三边构成的三角形,分别验证它们的面积值;(2)、问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从① ②或者② ① ;(3)、问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图, 的内切圆半径为 ,三角形三边长为 , , ,仍记 , 为三角形面积,则 .