2022-2023学年浙教版数学九上期末复习专题 直线与圆的位置关系
试卷更新日期:2022-11-19 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 面直角坐标系中,以点为圆心,为半径的圆一定与( )A、轴相交 B、轴相交 C、轴相切 D、轴相切2. 如图,在中, , , , 以点为圆心,以2cm的长为半径作圆,则与的位置关系是( )
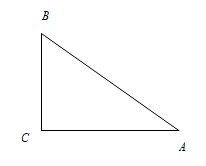 A、相离 B、相交 C、相切 D、相切或相交3. 圆的半径是7cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是( )A、相离 B、相切 C、相交 D、相交或相切4. 如图,已知是的直径,与相切于点 , 连接 , . 若 , 则的值为( )
A、相离 B、相交 C、相切 D、相切或相交3. 圆的半径是7cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是( )A、相离 B、相切 C、相交 D、相交或相切4. 如图,已知是的直径,与相切于点 , 连接 , . 若 , 则的值为( ) A、 B、 C、 D、5. 如图是一个钟表表盘,若连接整点2时与整点10时的、两点并延长,交过整点8时的切线于点 , 若切线长 , 表盘的半径长为( )
A、 B、 C、 D、5. 如图是一个钟表表盘,若连接整点2时与整点10时的、两点并延长,交过整点8时的切线于点 , 若切线长 , 表盘的半径长为( ) A、3 B、 C、 D、6. 如图,在平面直角坐标系中,过边长为1的正方形格点A、B、C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A、3 B、 C、 D、6. 如图,在平面直角坐标系中,过边长为1的正方形格点A、B、C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )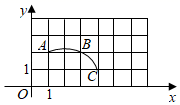 A、点(5,0) B、点(2,3) C、点(6,1) D、点(1,3)7. 如图,点B在⊙A上,点C在⊙A外,以下条件不能判定BC是⊙A切线的是( )
A、点(5,0) B、点(2,3) C、点(6,1) D、点(1,3)7. 如图,点B在⊙A上,点C在⊙A外,以下条件不能判定BC是⊙A切线的是( )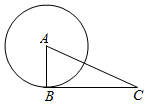 A、∠A=50°,∠C=40° B、∠B﹣∠C=∠A C、AB2+BC2=AC2 D、⊙A与AC的交点是AC中点8. 如图,OT是Rt△ABO的斜边AB上的高线,OA=OB,以O为圆心,OT为半径的圆交OA于点D,过点D作⊙O的切线CD,交AB于点C,已知OT=2,则BC的长为( )
A、∠A=50°,∠C=40° B、∠B﹣∠C=∠A C、AB2+BC2=AC2 D、⊙A与AC的交点是AC中点8. 如图,OT是Rt△ABO的斜边AB上的高线,OA=OB,以O为圆心,OT为半径的圆交OA于点D,过点D作⊙O的切线CD,交AB于点C,已知OT=2,则BC的长为( ) A、2 B、2 C、3 D、2+9. 根钢管放在V形架内,如图是其截面图,O为钢管的圆心,如果钢管的直径为20cm,∠MPN=60°,则OP的长度是( )
A、2 B、2 C、3 D、2+9. 根钢管放在V形架内,如图是其截面图,O为钢管的圆心,如果钢管的直径为20cm,∠MPN=60°,则OP的长度是( ) A、40cm B、40cm C、20cm D、20cm10. 如图,从圆外一点P引圆的两条切线PA,PB,A,B为切点,C为PB上的一点,连接CO交⊙O于点D,若 , , ,则⊙O的半径长是( )
A、40cm B、40cm C、20cm D、20cm10. 如图,从圆外一点P引圆的两条切线PA,PB,A,B为切点,C为PB上的一点,连接CO交⊙O于点D,若 , , ,则⊙O的半径长是( )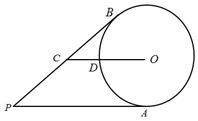 A、 B、 C、4 D、3
A、 B、 C、4 D、3二、填空题(每题4分,共24分)
-
11. 已知的半径 , 圆心到直线的距离是方程的解,则直线l与的位置关系是 .12. 如图所示,两个同心圆的半径之比为3:5,AB是大圆的直径,大圆的弦BC与小圆相切,若AC=12,则BC= .
 13. 如图,某雕塑MN位于河段OA上,游客P在步道上由点O出发沿OB方向行走.已知∠AOB=30°,MN=2OM=40m,当观景视角∠MPN最大时,游客P行走的距离OP是米.
13. 如图,某雕塑MN位于河段OA上,游客P在步道上由点O出发沿OB方向行走.已知∠AOB=30°,MN=2OM=40m,当观景视角∠MPN最大时,游客P行走的距离OP是米.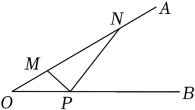 14. 如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD分别与⊙O相切于点C,D,若∠CPA=40°,则∠CAD的度数为°.
14. 如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD分别与⊙O相切于点C,D,若∠CPA=40°,则∠CAD的度数为°.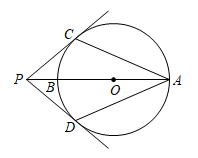 15. 如图,ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下AMN,则剪下的三角形的周长为 .
15. 如图,ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下AMN,则剪下的三角形的周长为 .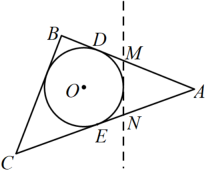 16. 如图,是一个小型花园,阴影部分为一个圆形水池,且与三边相切,已知 , , , 若从天空飘落下一片树叶恰好落入花园里,则落入水池的概率(取).
16. 如图,是一个小型花园,阴影部分为一个圆形水池,且与三边相切,已知 , , , 若从天空飘落下一片树叶恰好落入花园里,则落入水池的概率(取).
三、解答题(共8题,共66分)
-
17. 如图, , 分别与 相切于 两点,若 ,求 的度数.
 18. 如图,AD,BD是的弦, , 且 , 点C是BD的延长线上的一点, , 求证:AC是的切线.
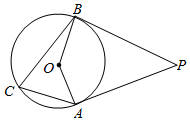
18. 如图,AD,BD是的弦, , 且 , 点C是BD的延长线上的一点, , 求证:AC是的切线.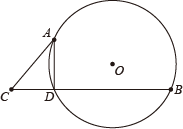 19. 如图,PA,PB是圆的切线,A,B为切点.
19. 如图,PA,PB是圆的切线,A,B为切点.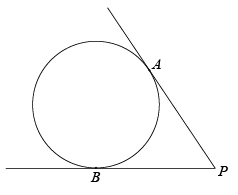 (1)、求作:这个圆的圆心O(用尺规作图,保留作图痕迹,不写作法和证明);(2)、在(1)的条件下,延长AO交射线PB于C点,若AC=4,PA=3,请补全图形,并求⊙O的半径.20. 如图,是的直径, , 是的两条切线,切点分别为B,C.延长、相交于点D.
(1)、求作:这个圆的圆心O(用尺规作图,保留作图痕迹,不写作法和证明);(2)、在(1)的条件下,延长AO交射线PB于C点,若AC=4,PA=3,请补全图形,并求⊙O的半径.20. 如图,是的直径, , 是的两条切线,切点分别为B,C.延长、相交于点D.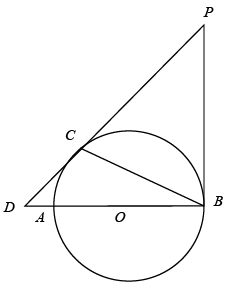 (1)、求证:;(2)、设的半径为2, , 求的长.21. 如图,D为⊙O上一点,点C在直径BA的延长线上,且CD2=CA·CB;
(1)、求证:;(2)、设的半径为2, , 求的长.21. 如图,D为⊙O上一点,点C在直径BA的延长线上,且CD2=CA·CB; (1)、求证:CD是⊙O的切线;(2)、过点B作⊙O的切线交CD的延长线于点E,若BC=10, ,求BE的长.22. 如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交 于点D , 过点D作DE//BC交AC的延长线于点E .
(1)、求证:CD是⊙O的切线;(2)、过点B作⊙O的切线交CD的延长线于点E,若BC=10, ,求BE的长.22. 如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交 于点D , 过点D作DE//BC交AC的延长线于点E .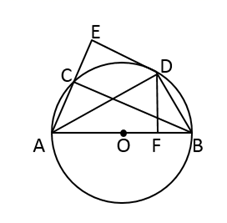 (1)、求证:DE是⊙O的切线;(2)、过点D作DF⊥AB于点F , 连接BD . 若OF=1 , BF=2,求sin∠DAB .23. 对于平面内的⊙C和⊙C外一点Q,给出如下定义:若过点Q的直线与⊙C存在公共点,记为点A,B,设 ,则称点A(或点B)是⊙C的“K相关依附点”,特别地,当点A和点B重合时,规定AQ=BQ, (或 ).
(1)、求证:DE是⊙O的切线;(2)、过点D作DF⊥AB于点F , 连接BD . 若OF=1 , BF=2,求sin∠DAB .23. 对于平面内的⊙C和⊙C外一点Q,给出如下定义:若过点Q的直线与⊙C存在公共点,记为点A,B,设 ,则称点A(或点B)是⊙C的“K相关依附点”,特别地,当点A和点B重合时,规定AQ=BQ, (或 ).已知在平面直角坐标系xOy中,Q(-1,0),C(1,0),⊙C的半径为r.
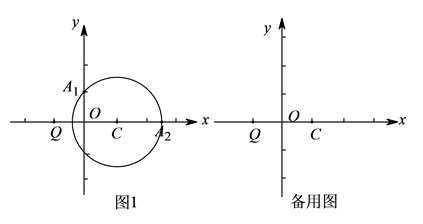 (1)、如图1,当 时,
(1)、如图1,当 时,①若A1(0,1)是⊙C的“k相关依附点”,求k的值.
②A2(1+ ,0)是否为⊙C的“2相关依附点”.
(2)、若⊙C上存在“k相关依附点”点M,①当r=1,直线QM与⊙C相切时,求k的值.
②当 时,求r的取值范围.
(3)、若存在r的值使得直线 与⊙C有公共点,且公共点时⊙C的“ 相关依附点”,直接写出b的取值范围.24. 如图,在矩形中, , , 点时的中点,是射线上一点,作交直线于点 , 过、、作 , 交于点 , 连接、 . (1)、当时,求的长;(2)、当点在线段上时,若与全等,求的半径;(3)、当与矩形各边所在的直线相切时,求的长.
(1)、当时,求的长;(2)、当点在线段上时,若与全等,求的半径;(3)、当与矩形各边所在的直线相切时,求的长.