2022-2023学年浙教版数学九上期末复习专题 解直角三角形
试卷更新日期:2022-11-19 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 如图,在 Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则 BC 的长是( )
 A、 B、4 C、8 D、42. 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比是1∶ , 则AC的长是( )
A、 B、4 C、8 D、42. 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比是1∶ , 则AC的长是( ) A、6米 B、12米 C、3米 D、6米3. 如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米, , 则河宽PT的长度是( )
A、6米 B、12米 C、3米 D、6米3. 如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米, , 则河宽PT的长度是( ) A、 B、 C、 D、4. 如图,是线段AB在投影面P上的正投影, , , 则投影的长为( )
A、 B、 C、 D、4. 如图,是线段AB在投影面P上的正投影, , , 则投影的长为( ) A、 B、 C、 D、5. 如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,垂直地面,垂足为点D, , 垂足为点C.设 , 下列关系式正确的是( )
A、 B、 C、 D、5. 如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,垂直地面,垂足为点D, , 垂足为点C.设 , 下列关系式正确的是( )
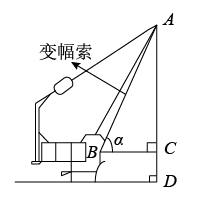 A、 B、 C、 D、6. 某简易房的示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AC的长为( )
A、 B、 C、 D、6. 某简易房的示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AC的长为( )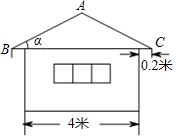 A、米 B、米 C、米 D、米7. 如图,线段AB与CD相交于点E,∠AED=45°,DE+AE=9,以AE和CE为边作AGCE,以DE和BE为边作EBFD,且AGCE和EBFD的面积都为3 , 若1<CE<3,则线段DF的取值范围是( )
A、米 B、米 C、米 D、米7. 如图,线段AB与CD相交于点E,∠AED=45°,DE+AE=9,以AE和CE为边作AGCE,以DE和BE为边作EBFD,且AGCE和EBFD的面积都为3 , 若1<CE<3,则线段DF的取值范围是( ) A、<DF<2 B、<DF<2 C、<DF<3 D、1<DF<38. 如图,在中, , , 点D是AC上一点,连接BD.若 , , 则CD的长为( )
A、<DF<2 B、<DF<2 C、<DF<3 D、1<DF<38. 如图,在中, , , 点D是AC上一点,连接BD.若 , , 则CD的长为( ) A、 B、3 C、 D、29. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )
A、 B、3 C、 D、29. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )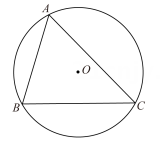 A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)10. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )
A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)10. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )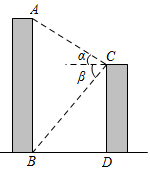 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 已知某斜面的坡度为1: , 那么这个斜面的坡角等于度.12. 如图,A位于学校主教学楼P南偏东45°方向,且距离教学楼60米,小明同学从这里出发沿着正北方向走了一段时间后,到达位于主教学楼北偏东30°方向的综合楼B处,此时小明同学一共走的距离为米.
 13. 小丽想测量学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为30°,测倾器到旗杆底部的距离为12米,测倾器的高度为1.6米,那么旗杆的高度为米(结果保留根号).
13. 小丽想测量学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为30°,测倾器到旗杆底部的距离为12米,测倾器的高度为1.6米,那么旗杆的高度为米(结果保留根号). 14. 如图,在Rt△ABC中,∠ACB=90°,AC<BC,CD平分∠ACB交AB于点D,以DB为直径作⊙O,分别交CD,BC于点E,F,连结BE,EF.则∠EBF=度;若DE=DC, BC=8,则EF的长为
14. 如图,在Rt△ABC中,∠ACB=90°,AC<BC,CD平分∠ACB交AB于点D,以DB为直径作⊙O,分别交CD,BC于点E,F,连结BE,EF.则∠EBF=度;若DE=DC, BC=8,则EF的长为 15. 如图,在矩形 中,点 在边 上, 于点 ,若 , ,则 的值为.
15. 如图,在矩形 中,点 在边 上, 于点 ,若 , ,则 的值为. 16. 图1是郑州的网红打卡点 “戒指桥”, 其数学模型如图2所示. 线段是其中一条拉索, 点在圆上, 点是圆和水平桥面的交点. 小明测得 , 且在 B点和点观测点的仰角均为 , 则点到桥面的距离为 , “戒指” 的半径为 .
16. 图1是郑州的网红打卡点 “戒指桥”, 其数学模型如图2所示. 线段是其中一条拉索, 点在圆上, 点是圆和水平桥面的交点. 小明测得 , 且在 B点和点观测点的仰角均为 , 则点到桥面的距离为 , “戒指” 的半径为 .
三、解答题(共8题,共66分)
-
17. 如图,网格中的每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上.

⑴在图中画出以AB为一边的菱形ABCD,点C和点D在小正方形顶点上;
⑵在图中画出以AB为斜边的直角三角形ABE,点E在小正方形顶点上,且 , 连接CE,请直接写出线段CE的长.
18. 某型号飞机的机翼形状如图所示,根据图中数据计算的长度(结果保留小数点后一位,). 19. 如图,某超市计划将门前的部分楼梯改造成无障碍通道.已知楼梯共有五级均匀分布的台阶,高AB=0.75m,斜坡AC的坡比为1:2,将要铺设的通道前方有一井盖,井盖边缘离楼梯底部的最短距离ED=2.55m.为防止通道遮盖井盖,所铺设通道的坡角不得小于多少度?(结果精确到1)
19. 如图,某超市计划将门前的部分楼梯改造成无障碍通道.已知楼梯共有五级均匀分布的台阶,高AB=0.75m,斜坡AC的坡比为1:2,将要铺设的通道前方有一井盖,井盖边缘离楼梯底部的最短距离ED=2.55m.为防止通道遮盖井盖,所铺设通道的坡角不得小于多少度?(结果精确到1)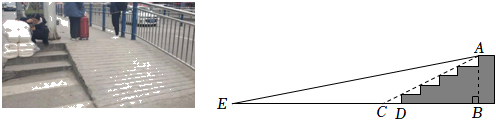
(参考数据表)
计算器按键顺序
计算结果(已精确到0.001)

11.310

0.003
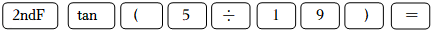
14.744

0.005
20. 如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E。CF⊥BD于点F,连接AF,CE。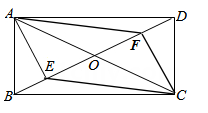 (1)、求证:四边形AECF是平行四边形;(2)、若∠AOB=60°,AC=8,求四边形AFCE的面积。21. 为传承运河文明,弘扬民族精神,枣庄市政府重建了台儿庄古城.某校“综合与实践”小组开展了测量台儿庄古城城门楼(如图①)高度的实践活动,请你帮他们完成下面的实践报告.
(1)、求证:四边形AECF是平行四边形;(2)、若∠AOB=60°,AC=8,求四边形AFCE的面积。21. 为传承运河文明,弘扬民族精神,枣庄市政府重建了台儿庄古城.某校“综合与实践”小组开展了测量台儿庄古城城门楼(如图①)高度的实践活动,请你帮他们完成下面的实践报告.测量台儿庄古城城门楼高度的实践报告
活动课题
测量台儿庄古城城门楼高度
活动目的
运用三角函数知识解决实际问题
活动工具
测角仪、皮尺等测量工具
方案示意图
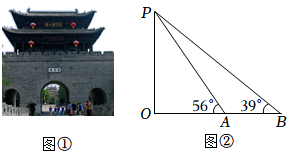
测量步骤
如图②
⑴利用测角仪站在B处测得城门楼最高点P的仰角为39°;
⑵前进了10米到达A处(选择测点A,B与O在同一水平线上,A,B两点之间的距离可直接测得,测角仪高度忽略不计),在A处测得P点的仰角为56°.
参考数据
sin39°≈0.6,cos39°≈0.8,tan39°≈0.8,sin56°≈0.8,cos56°≈0.6,tan56°≈1.5.
计算城门楼PO的高度(结果保留整数)
22. 2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情.如图是某滑雪场的横截面示意图,雪道分为AB,BC两部分,小明同学在C点测得雪道BC的坡度i=1:2.4,在A点测得B点的俯角∠DAB=30°.若雪道AB长为270m,雪道BC长为260m.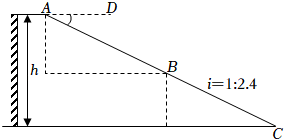 (1)、求该滑雪场的高度h;(2)、据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3 , 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.23. 某沿海城市O,每年都会受到几次台风侵袭,台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风景,有极强的破坏力.某次,据气象观察,距该城市正南方向的A处有一台风中心,中心最大风力为12级,每远离台风中心 千米,风力就会减弱一级,该台风中心正以20千米/时的速度沿北偏东45°方向向B处移动,且台风中心风力不变,若城市受到风力达到或超过6级,则称受台风影响.
(1)、求该滑雪场的高度h;(2)、据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3 , 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.23. 某沿海城市O,每年都会受到几次台风侵袭,台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风景,有极强的破坏力.某次,据气象观察,距该城市正南方向的A处有一台风中心,中心最大风力为12级,每远离台风中心 千米,风力就会减弱一级,该台风中心正以20千米/时的速度沿北偏东45°方向向B处移动,且台风中心风力不变,若城市受到风力达到或超过6级,则称受台风影响.
(注:结果四舍五入保留整数,参考数据: , )
(1)、若该城市受此次台风影响共持续了10小时(即台风中心从C处移动到D处),那么受到台风影响的最大风力为几级?(2)、求该城市O到A处的距离.24. 图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,托板长AB=115mm,支撑板长CD=70mm,且CB=35mm,托板AB可绕点C转动,且∠CDE=60°。(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7) (1)、求点C到直线DE的距离(计算结果保留根号);(2)、若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);(3)、为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在DE上,则CD旋转的度数为 . (直接写出结果)
(1)、求点C到直线DE的距离(计算结果保留根号);(2)、若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);(3)、为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在DE上,则CD旋转的度数为 . (直接写出结果)