2022-2023学年浙教版数学九上期末复习专题 锐角三角形
试卷更新日期:2022-11-19 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 在直角ΔABC中,已知∠C=90°, ,求cosA=( )A、 B、 C、 D、2. 已知sin42°≈ , 则cos48°的值约为( )A、 B、 C、 D、3. 在中, , 都是锐角,且 , , 则的形状是( )A、直角三角形 B、钝角三角形 C、等边三角形 D、不能确定4. 在Rt△ABC中,∠C=90°,若sin∠A= , 则cosB=( )A、 B、 C、 D、5. 在中, , 如果 , 那么的值为( )A、 B、 C、 D、6. 把Rt△ABC各边的长度都扩大3倍得到Rt△A′B′C′,那么锐角∠A、∠A′的余弦值的关系是( )A、cosA=cosA′ B、cosA=3cosA′ C、3cosA=cosA′ D、不能确定7. 下列计算中错误的是( )A、 B、 C、 D、8. 若用我们数学课本上采用的科学计算器计算 , 按键顺序正确的是( )A、
 B、
B、 C、
C、 D、
D、 9. 如果锐角A的度数是25°,那么下列结论中正确的是( )A、 B、 C、 D、10. 如图,在圆O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
9. 如果锐角A的度数是25°,那么下列结论中正确的是( )A、 B、 C、 D、10. 如图,在圆O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( ) A、16 B、20 C、18 D、22
A、16 B、20 C、18 D、22二、填空题(每题3分,共18分)
-
11. 在中, , 若 , 则 .12. 设α是锐角,如果tanα=3,那么cotα= .13. α是锐角,若sinα=cos15°,则α=°.14. 比较大小:sin35°cos45°.15. 如图是北京冬奥会开幕式的巨型雪花状主火炬塔,此设计体现了环保低碳理念,它的主体形状呈正六边形,若点A,B,C是正六边形的三个顶点,则.
 16. 如图,的顶点是正方形网格的格点,则的值为 .
16. 如图,的顶点是正方形网格的格点,则的值为 .
三、解答题(共10题,共72分)
-
17. 计算:(1)、;(2)、 .18. 先化简,再求值: , 其中 , .19. 已知∠A为锐角且sinA= ,则4sin2A-4sinAcosA+cos2A的值是多少。20. 用计算器求图中 的正弦值、余弦值和正切值.
 21. 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
21. 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
⑴请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
⑵以点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正切值为 ▲ .
22.(1)、完成下列表格,并回答下列问题,锐角
(2)、当锐角 逐渐增大时, 的值逐渐 , 的值逐渐 , 的值逐渐 .(3)、 , ;(4)、 ;(5)、 ;(6)、若 ,则锐角 .23. 如图,根据图中数据完成填空,再按要求答题: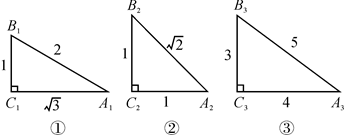 (1)、sin2A1+sin2B1=;sin2A2+sin2B2=;sin2A3+sin2B3=;(2)、观察上述等式,猜想:在Rt△ABC中,∠C=90°.都有:sin2A+sin2B=;(3)、如图,在Rt△ABC中,∠C=90°,∠A , ∠B , ∠C的对边分别是a , b , c;利用三角函数的定义和勾股定理,证明你的猜想;
(1)、sin2A1+sin2B1=;sin2A2+sin2B2=;sin2A3+sin2B3=;(2)、观察上述等式,猜想:在Rt△ABC中,∠C=90°.都有:sin2A+sin2B=;(3)、如图,在Rt△ABC中,∠C=90°,∠A , ∠B , ∠C的对边分别是a , b , c;利用三角函数的定义和勾股定理,证明你的猜想;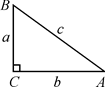 (4)、已知:∠A+∠B=90°,且sinA= , 求sinB.24. 如图,在四边形 中, , , , 交 于点 ,过点 作 ,垂足为 ,且 .
(4)、已知:∠A+∠B=90°,且sinA= , 求sinB.24. 如图,在四边形 中, , , , 交 于点 ,过点 作 ,垂足为 ,且 . (1)、求证:四边形 是菱形;(2)、若 ,求 的面积.25. 如图,AB是⊙O的直径,弦CD⊥AB,点E是 上一点,点D关于CE的对称点F恰好落在DA的延长线上,连结CF.
(1)、求证:四边形 是菱形;(2)、若 ,求 的面积.25. 如图,AB是⊙O的直径,弦CD⊥AB,点E是 上一点,点D关于CE的对称点F恰好落在DA的延长线上,连结CF. (1)、求证:∠BAD=∠ECF.(2)、若tan∠BAD= ,AF=9,求⊙O的半径.26. 如图,雨伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC.当伞收紧时,点D与点M重合,且点A,E(F),D 在同一条直线上.已知伞骨的部分长度如下(单位:cm):
(1)、求证:∠BAD=∠ECF.(2)、若tan∠BAD= ,AF=9,求⊙O的半径.26. 如图,雨伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC.当伞收紧时,点D与点M重合,且点A,E(F),D 在同一条直线上.已知伞骨的部分长度如下(单位:cm):伞骨
DE
DF
AE
AF
AB
AC
长度
36
36
36
36
86
86
 (1)、求AM的长.(2)、当伞撑开时,量得∠BAC=110°,求AD的长(结果精确到1cm).参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.428.
(1)、求AM的长.(2)、当伞撑开时,量得∠BAC=110°,求AD的长(结果精确到1cm).参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.428.